Spectral Graph Theory

Quiz

Spectral Graph Theory

Spectral Graph Theory is a branch of graph theory that focuses on studying the properties of graphs by analyzing the eigenvalues and eigenvectors of matrices associated with the graph.

The most commonly studied matrices are the adjacency matrix and the Laplacian matrix, which provide important information about the structure and behavior of the graph.

By analyzing the spectrum (eigenvalues) of these matrices, we can have details of various graph properties such as connectivity, clustering, graph partitioning, and even the behavior of diffusion processes on the graph.

Adjacency Matrix and Eigenvalues

The adjacency matrix of a graph G = (V, E) is a square matrix A where each entry A(i, j) represents the presence (or weight) of an edge between vertices i and j. In an undirected graph, the adjacency matrix is symmetric.

The eigenvalues of the adjacency matrix contain important information about the graph's structure. For example, the largest eigenvalue can provide details of the graph's connectivity, while the multiplicity of the eigenvalue 0 can help identify the number of disconnected components.

Formally, if A is the adjacency matrix of a graph, and v is a vector (called an eigenvector), then −

A * v =  * v

Where is the eigenvalue corresponding to eigenvector v.

Example: Eigenvalues of the Adjacency Matrix

Consider a simple graph with 3 vertices and 3 edges forming a cycle:

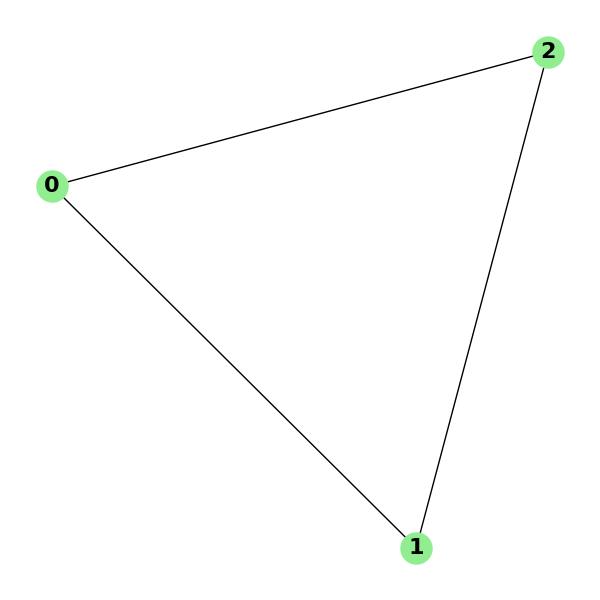
Adjacency matrix of G:
[[0, 1, 0],
 [1, 0, 1],
 [0, 1, 0]]

Eigenvalues of the matrix: [2, -1, -1]

In this case, the adjacency matrix has eigenvalues 2, -1, and -1, which indicate specific structural properties of the graph.

Laplacian Matrix and Spectral Properties

The Laplacian matrix of a graph is defined as L = D - A, where D is the degree matrix (a diagonal matrix with vertex degrees as diagonal entries) and A is the adjacency matrix. The Laplacian matrix is useful in analyzing graph connectivity and the behavior of diffusion processes.

Like the adjacency matrix, the Laplacian matrix also has eigenvalues that provide information about the graph. The smallest eigenvalue is always 0, and its multiplicity indicates the number of connected components in the graph. A graph is connected if and only if the multiplicity of the eigenvalue 0 is 1.

Example: Eigenvalues of the Laplacian Matrix

For the same graph as above (the cycle graph with 3 vertices), the Laplacian matrix is −

Degree matrix D:
[[1, 0, 0],
 [0, 2, 0],
 [0, 0, 1]]

Laplacian matrix L:
[[ 1, -1,  0],
 [-1,  2, -1],
 [ 0, -1,  1]]

Eigenvalues of the Laplacian matrix: [0, 2, 2]

The eigenvalues 0, 2, and 2 indicate that the graph is connected (since the multiplicity of the eigenvalue 0 is 1). The other eigenvalues give details of the graph's structure and connectivity.

Applications of Spectral Graph Theory

Spectral Graph Theory has various applications in computer science, physics, biology, and network analysis. Some of the most important applications are −

Graph Partitioning: Spectral methods can be used to divide a graph into smaller, more manageable subgraphs. This is particularly useful in parallel computing and social network analysis.
Graph Clustering: The eigenvalues and eigenvectors of the Laplacian matrix can be used to identify clusters or communities within a graph.
Network Synchronization: Spectral methods can help to analyze synchronization phenomena in networks, such as those seen in neural networks or electrical circuits.
Graph Traversal and Diffusion: The Laplacian matrix is used to model random walks and diffusion processes on graphs, which can be applied to areas like information spread, epidemic modeling, and diffusion in social networks.

Cheeger's Inequality

Cheeger's Inequality connects the spectral properties of the Laplacian matrix with the structural properties of a graph. It provides a bound on the graph's "conductance" (a measure of its connectivity) using the second-smallest eigenvalue of the Laplacian matrix.

The conductance of a graph is a measure of how well connected the graph is, and Cheeger's inequality states that:

  ₂ / 2

Where ₂ is the second-smallest eigenvalue of the Laplacian matrix. This inequality helps in understanding the sparsity and connectivity of a graph.

Spectral Graph Theory and Random Walks

Random walks are processes in which an object moves from one vertex to another based on certain probabilities. Spectral graph theory is used to study the behavior of random walks on graphs, particularly in the context of the Laplacian matrix.

The eigenvalues and eigenvectors of the Laplacian matrix plays an important role in determining the mixing time and convergence rate of random walks. A lower second-smallest eigenvalue indicates slower mixing, meaning the random walk takes longer to reach a stationary distribution.

Graph Signal Processing

Graph signal processing is an emerging field that leverages spectral graph theory to analyze signals defined on the vertices of a graph. This approach generalizes traditional signal processing techniques to irregular, non-Euclidean domains, such as social networks, sensor networks, and brain networks.

In this context, the eigenvalues and eigenvectors of the graph Laplacian are used to filter and analyze graph signals. For example, the eigenvectors can serve as "basis functions" for the graph, enabling signal processing techniques like filtering, smoothing, and denoising.

Challenges in Spectral Graph Theory

While spectral graph theory provides powerful tools for analyzing graphs, it still faces several challenges −

Large Graphs: Calculating the eigenvalues and eigenvectors of large graphs can be computationally expensive, especially for graphs with millions of vertices and edges.
Spectral Clustering: Determining the best way to use the spectral information to identify meaningful clusters or partitions in large and complex graphs remains an open problem.
Dynamic Graphs: Spectral graph theory mainly deals with static graphs, and extending it to dynamic graphs (where the graph structure changes over time) is an ongoing area of research.

Print Page