Graph Theory - Push-Relabel Algorithm

Quiz

Push-Relabel Algorithm

The Push-Relabel algorithm, also known as the Preflow-Push algorithm, is used to compute the maximum flow in a flow network.

Unlike the Edmonds-Karp algorithm, which uses augmenting paths, the Push-Relabel algorithm maintains a preflow and iteratively pushes excess flow through the network while adjusting vertex heights (or labels). This approach allows the algorithm to achieve good performance on various types of networks, particularly those with high connectivity.

The Push-Relabel algorithm relies on the following important concepts −

Preflow: A function that may temporarily violate the flow conservation property by allowing excess flow at vertices.
Excess Flow: The amount of flow entering a vertex minus the amount of flow leaving the vertex.
Height Function: A function that assigns a height (or label) to each vertex to ensure that flow is pushed from higher to lower heights.

Overview of Push-Relabel Algorithm

The Push-Relabel algorithm uses two main operations, "push" and "relabel", to adjust the flow in the network −

Push Operation: The push operation pushes excess flow from a node to one of its neighbors, provided there is available capacity and the neighboring node is at a lower height.
Relabel Operation: The relabel operation increases the height of a node when it cannot push flow to any of its neighbors, enabling future pushes.

The algorithm maintains a height function and an excess flow function to guide these operations. The height function helps ensure that the flow moves towards the sink, while the excess flow function tracks the amount of flow that needs to be redistributed.

Properties of Push-Relabel Algorithm

The Push-Relabel algorithm has several important properties and characteristics, they are −

Local Operations: The algorithm uses local operations (push and relabel) to adjust the flow, making it highly efficient in practice.
Preflow-Push Approach: The algorithm starts with a preflow that may violate flow conservation and adjusts it to satisfy conservation constraints.
Guaranteed Termination: The algorithm is guaranteed to terminate with a maximum flow in a finite number of steps.
Efficient on Sparse Graphs: The Push-Relabel algorithm is particularly effective on large, sparse graphs.

Steps of Push-Relabel Algorithm

To better understand how the Push-Relabel algorithm works, let us break it down into individual steps −

Initialization

In the initialization step, the algorithm sets the height of the source vertex to the number of vertices in the graph, ensuring it is higher than any other vertex. The initial preflow is created by sending as much flow as possible from the source to its neighbors:

def initialize_preflow(graph, source):
   n = len(graph)
   height = [0] * n
   excess = [0] * n
   height[source] = n
   for v in range(n):
      if graph[source][v] > 0:
         excess[v] = graph[source][v]
         graph[v][source] = graph[source][v]
         graph[source][v] = 0
   return height, excess

In the above code, the height of the source vertex is set to the number of vertices, and excess flow is pushed to its neighbors.

Push Operation

The push operation attempts to send excess flow from a vertex to its neighbors. This is only possible if the height of the current vertex is greater than the height of the neighbor, and there is available residual capacity:

def push(graph, u, v, excess, height):
   send_flow = min(excess[u], graph[u][v])
   excess[u] -= send_flow
   excess[v] += send_flow
   graph[u][v] -= send_flow
   graph[v][u] += send_flow

In this code, flow is pushed from vertex u to vertex v, updating the excess flow and the residual capacities accordingly.

Relabel Operation

If no push operation is possible from a vertex with excess flow, the vertex's height is increased to enable further push operations. The new height is set to one more than the minimum height of its neighbors with available capacity:

def relabel(graph, u, height):
   min_height = float('inf')
   for v in range(len(graph)):
      if graph[u][v] > 0:
         min_height = min(min_height, height[v])
   height[u] = min_height + 1

This code increases the height of vertex u based on the heights of its neighbors with residual capacity.

Discharge Operation

The discharge operation repeatedly applies push and relabel operations to a vertex until it no longer has excess flow:

def discharge(graph, u, excess, height):
   while excess[u] > 0:
      for v in range(len(graph)):
         if graph[u][v] > 0 and height[u] > height[v]:
            push(graph, u, v, excess, height)
            if excess[u] == 0:
               break
      if excess[u] > 0:
         relabel(graph, u, height)

This function ensures that vertex u is repeatedly pushed and relabeled until its excess flow is reduced to zero.

Complete Python Implementation

The complete implementation of the Push-Relabel algorithm involves initializing the preflow, and then repeatedly discharging vertices with excess flow until no further pushes are possible −

def initialize_preflow(graph, source):
   n = len(graph)
   height = [0] * n
   excess = [0] * n
   height[source] = n
   for v in range(n):
      if graph[source][v] > 0:
         excess[v] = graph[source][v]
         graph[v][source] = graph[source][v]
         graph[source][v] = 0
   return height, excess

def push(graph, u, v, excess, height):
   send_flow = min(excess[u], graph[u][v])
   excess[u] -= send_flow
   excess[v] += send_flow
   graph[u][v] -= send_flow
   graph[v][u] += send_flow

def relabel(graph, u, height):
   min_height = float('inf')
   for v in range(len(graph)):
      if graph[u][v] > 0:
         min_height = min(min_height, height[v])
   height[u] = min_height + 1

def discharge(graph, u, excess, height):
   while excess[u] > 0:
      for v in range(len(graph)):
         if graph[u][v] > 0 and height[u] > height[v]:
            push(graph, u, v, excess, height)
            if excess[u] == 0:
               break
      if excess[u] > 0:
         relabel(graph, u, height)

def push_relabel(graph, source, sink):
   height, excess = initialize_preflow(graph, source)
   vertices = len(graph)
    
   # Push and relabel until there is no excess flow left
   while any(excess[i] > 0 for i in range(vertices) if i != source and i != sink):
      for u in range(vertices):
         if u != source and u != sink and excess[u] > 0:
            discharge(graph, u, excess, height)
    
   return excess, graph

# Example graph as an adjacency matrix (capacity of the edges)
graph = [
   [0, 10, 5, 0, 0, 0],
   [0, 0, 15, 10, 0, 0],
   [0, 0, 0, 10, 10, 0],
   [0, 0, 0, 0, 15, 10],
   [0, 0, 0, 0, 0, 10],
   [0, 0, 0, 0, 0, 0]
]

source = 0
sink = 5

excess, final_graph = push_relabel(graph, source, sink)

# Calculating the maximum flow by summing the excess at the sink node
max_flow = excess[sink]

# Printing the result
print("Final Excess Flow: ", excess)
print("Final Residual Graph: ", final_graph)
print("Maximum Possible Flow: ", max_flow)

In this implementation, active vertices with excess flow are processed until no more push operations can be performed. The maximum flow is obtained from the sum of the flow into the sink vertex.

Final Excess Flow:  [0, 0, 0, 0, 0, 15]
Final Residual Graph:  [[0, 0, 0, 0, 0, 0], [10, 0, 10, 5, 0, 0], [5, 5, 0, 0, 10, 0], [0, 5, 10, 0, 5, 5], [0, 0, 0, 10, 0, 0], [0, 0, 0, 5, 10, 0]]
Maximum Possible Flow:  15

Example

Consider the following flow network −

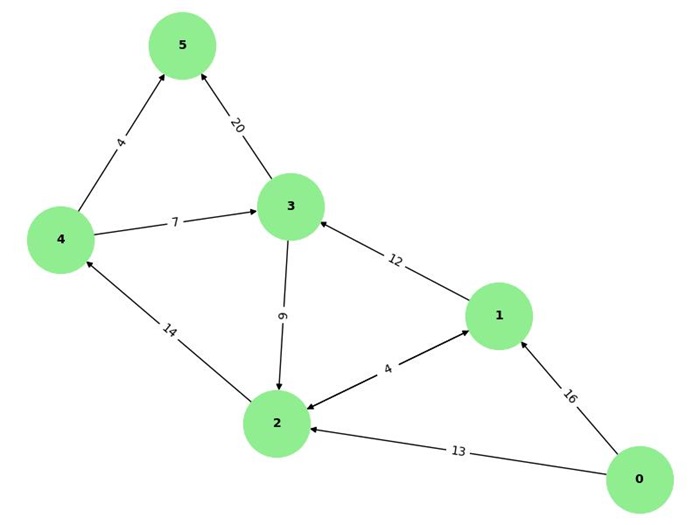
Let us apply the Push-Relabel algorithm step by step −

Initialize the preflow and heights:

graph = [[0, 16, 13, 0, 0, 0],
         [0, 0, 10, 12, 0, 0],
         [0, 4, 0, 0, 14, 0],
         [0, 0, 9, 0, 0, 20],
         [0, 0, 0, 7, 0, 4],
         [0, 0, 0, 0, 0, 0]]
source = 0
sink = 5

max_flow = push_relabel_max_flow(graph, source, sink)
print(f"The maximum flow is {max_flow}")

Perform push and relabel operations until no more excess flow is present.

After applying the algorithm, we obtain the maximum flow of 23 units from the source to the sink.

Complexity Analysis

The Push-Relabel algorithm has a time complexity of O(V^2E) in the worst case, where V is the number of vertices and E is the number of edges. This complexity is derived from the fact that each push operation can be performed at most O(VE) times, and each relabel operation can be performed at most O(V²) times.

The space complexity of this algorithm is O(V + E), where V represents the number of vertices and E denotes the number of edges in the graph. This complexity arises from the need to store the flow network, preflows, heights, and active nodes.

Print Page