Graph Theory - Graph Isomorphism

---

---

Graph Isomorphism

Graph isomorphism determines whether two graphs are structurally the same or not. If two graphs are isomorphic, it means there is a one-to-one correspondence between their vertices and edges that preserves the connectivity of the graphs.

In other words, if one graph can be transformed into another by simply re-labeling the vertices, they are considered isomorphic.

Two graphs G1 and G2 are said to be isomorphic if −

• Their number of components (vertices and edges) are the same.
• Their edge connectivity is retained.

In short, out of the two isomorphic graphs, one is a tweaked version of the other. An unlabeled graph also can be thought of as an isomorphic graph.

There exists a function 'f' from vertices of G1 to vertices of G2 [f: V(G1) V(G2)], such that −

• Case (i): f is a bijection (both one-to-one and onto).
• Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the edge {f(U), f(V)} ∈ G2, then G1 G2.

Important Conditions for Graph Isomorphism

Two graphs G₁ and G₂ are isomorphic (G₁ G₂) if the following conditions are met:

• The number of vertices in G₁ and G₂ must be the same, i.e., |V(G₁)| = |V(G₂)|.
• The number of edges in G₁ and G₂ must also be equal, i.e., |E(G₁)| = |E(G₂)|.
• The degree sequences of G₁ and G₂ must match, meaning the list of vertex degrees in both graphs must be identical.
• If a set of vertices {V₁, V₂, ..., V_k} forms a cycle of length k in G₁, then the corresponding set of vertices {f(V₁), f(V₂), ..., f(V_k)} in G₂ must also form a cycle of the same length k.

While these conditions are necessary for G₁ and G₂ to be isomorphic, they are not sufficient by themselves to definitively prove isomorphism.

Additional important properties for graph isomorphism are −

• Two simple graphs G₁ and G₂ are isomorphic (G₁ G₂) if and only if their reduced forms (after removing specific vertices or edges) are also isomorphic.
• If the adjacency matrices of G₁ and G₂ are identical after reordering their rows and columns, the graphs are isomorphic.
• G₁ G₂ if and only if any corresponding subgraphs of G₁ and G₂ (obtained by deleting certain vertices and their edges in both graphs) are isomorphic.

Example

Determine which of the following graphs are isomorphic.

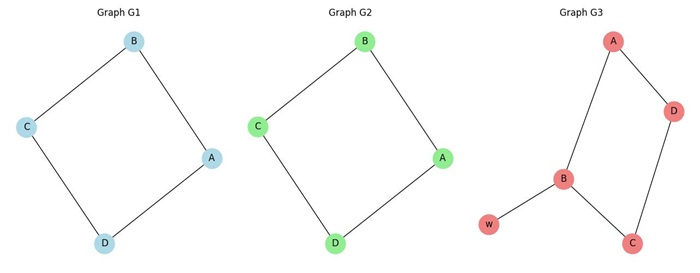
Degree sequence of G1: [2, 2, 2, 2]
Degree sequence of G2: [2, 2, 2, 2]
Degree sequence of G3: [1, 2, 2, 2, 3]
Are G1 and G2 isomorphic? True
Are G1 and G3 isomorphic? False
Are G2 and G3 isomorphic? False

• Here, in graph G₃, the vertex B has a degree of 3, whereas all other vertices in G₁ and G₂ have a degree of 2. This difference in degree sequence indicates that G₃ is not isomorphic to either G₁ or G₂.

Now, consider the complements of graphs G₁ and G₂ −

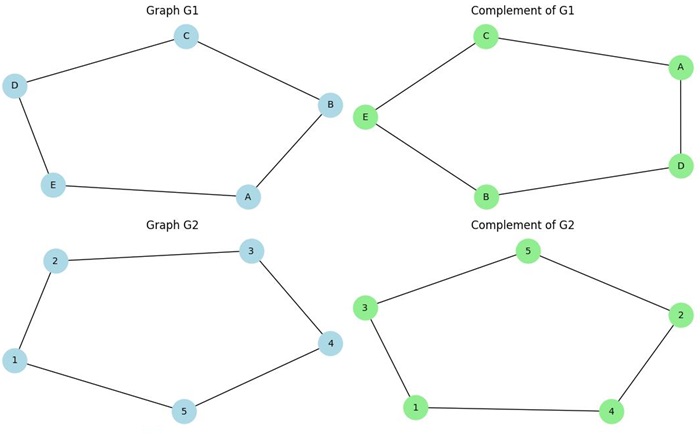
• The complements of G₁ and G₂ are isomorphic, i.e., G₁ G₂. Therefore, the original graphs G₁ and G₂ are also isomorphic, i.e., G₁ G₂.

Properties of Graph Isomorphism

Graph isomorphism has several important properties that can help in determining whether two graphs are isomorphic −

• Bijective Mapping: Graph isomorphism relies on a bijective mapping between the vertices of two graphs. This mapping ensures that every vertex in one graph corresponds to exactly one unique vertex in the other graph and vice versa.
• Preserved Adjacency: The mapping should preserve the adjacency of the vertices. If two vertices are connected by an edge in one graph, their corresponding vertices in the other graph must also be connected by an edge.
• Graph Invariants: Some graph properties, such as the number of vertices, edges, degree sequence, and spectrum, must be the same in isomorphic graphs. If these properties differ between two graphs, they cannot be isomorphic.
• Subgraph Isomorphism: A graph isomorphism can be extended to subgraphs. If two graphs are isomorphic, their corresponding subgraphs will also be isomorphic.

Checking Graph Isomorphism

Determining if two graphs are isomorphic can be challenging, especially for large graphs. Although there is no known polynomial-time algorithm for general graph isomorphism, we can use several methods and heuristics to check for isomorphism −

• Naive Algorithm: The simplest approach is to generate all possible vertex mappings between the two graphs and check if the adjacency relations are preserved. However, this method has exponential time complexity, making it inefficient for large graphs.
• Canonical Forms: To simplify isomorphism testing, graphs can be converted into a unique canonical form (a unique representation). If two graphs share the same canonical form, they are isomorphic. Techniques like graph canonization are used to achieve this representation.
• Graph Invariants: Comparing graph invariants such as the number of vertices, edges, and degree sequences can quickly rule out non-isomorphic graphs. If these properties differ, the graphs cannot be isomorphic.
• Adjacency Matrix Comparison: For smaller graphs, adjacency matrices can be compared. These matrices represent the presence or absence of edges between vertices. If the matrices match after row and column permutations, the graphs are isomorphic.
• Refinement Algorithms: Algorithms like the Weisfeiler-Lehman algorithm refine vertex labels iteratively based on neighboring vertices. If the final labeling is same for both graphs, they are isomorphic.

Isomorphism Between Two Simple Graphs

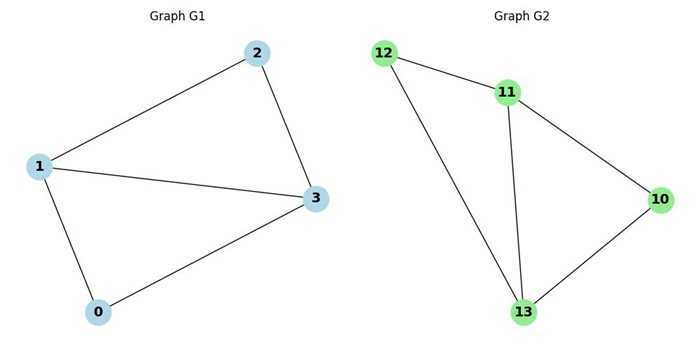
Consider two graphs, G₁ and G₂, each consisting of four vertices and five edges. By examining their structures, we observe that the degree sequence of both graphs is the same (i.e., two vertices of degree 3 and two vertices of degree 2).

Therefore, we can check whether there is a mapping between the vertices that preserves the adjacency relationships. If such a mapping exists, then the two graphs are isomorphic.

Are G1 and G2 isomorphic? True
Degree sequence of G1: [2, 2, 3, 3]
Degree sequence of G2: [2, 2, 3, 3]
Do they have the same degree sequence? True

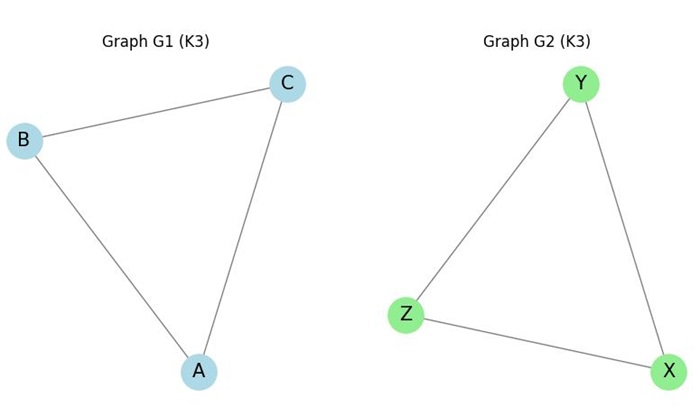
Isomorphism of a Complete Graph

Consider two complete graphs, K₃ and K₃ (the complete graph on 3 vertices).

It is obvious that any two complete graphs with the same number of vertices are isomorphic because they both have all possible edges between the vertices. The graph isomorphism is simply a re-labeling of the vertices.

Non-Isomorphic Graphs

Consider two graphs, G₁ and G₂, where G₁ has four vertices with a degree sequence of (3, 2, 2, 1), while G₂ has a degree sequence of (2, 2, 2, 2).

Since the degree sequences are not identical, we can immediately conclude that the graphs are not isomorphic, without needing to check further properties.

Challenges in Graph Isomorphism

Although graph isomorphism is a well-studied problem, it remains challenging for certain types of graphs −

• Complexity: The graph isomorphism problem is classified as NP (nondeterministic polynomial) for general graphs. However, there is no known polynomial-time algorithm that works for all graph classes, making the problem difficult for large graphs.
• Large Graphs: For large graphs, the huge number of possible vertex mappings can make the isomorphism check computationally expensive. As the size of the graph increases, the problem becomes increasingly harder to solve.
• No Universal Algorithm: While many specialized algorithms exist for certain classes of graphs (e.g., planar graphs, trees), there is no universal algorithm that works efficiently for all graphs.