
- Graph Theory - Home
- Graph Theory - Introduction
- Graph Theory - History
- Graph Theory - Fundamentals
- Graph Theory - Applications
- Types of Graphs
- Graph Theory - Types of Graphs
- Graph Theory - Simple Graphs
- Graph Theory - Multi-graphs
- Graph Theory - Directed Graphs
- Graph Theory - Weighted Graphs
- Graph Theory - Bipartite Graphs
- Graph Theory - Complete Graphs
- Graph Theory - Subgraphs
- Graph Theory - Trees
- Graph Theory - Forests
- Graph Theory - Planar Graphs
- Graph Theory - Hypergraphs
- Graph Theory - Infinite Graphs
- Graph Theory - Random Graphs
- Graph Representation
- Graph Theory - Graph Representation
- Graph Theory - Adjacency Matrix
- Graph Theory - Adjacency List
- Graph Theory - Incidence Matrix
- Graph Theory - Edge List
- Graph Theory - Compact Representation
- Graph Theory - Incidence Structure
- Graph Theory - Matrix-Tree Theorem
- Graph Properties
- Graph Theory - Basic Properties
- Graph Theory - Coverings
- Graph Theory - Matchings
- Graph Theory - Independent Sets
- Graph Theory - Traversability
- Graph Theory Connectivity
- Graph Theory - Connectivity
- Graph Theory - Vertex Connectivity
- Graph Theory - Edge Connectivity
- Graph Theory - k-Connected Graphs
- Graph Theory - 2-Vertex-Connected Graphs
- Graph Theory - 2-Edge-Connected Graphs
- Graph Theory - Strongly Connected Graphs
- Graph Theory - Weakly Connected Graphs
- Graph Theory - Connectivity in Planar Graphs
- Graph Theory - Connectivity in Dynamic Graphs
- Special Graphs
- Graph Theory - Regular Graphs
- Graph Theory - Complete Bipartite Graphs
- Graph Theory - Chordal Graphs
- Graph Theory - Line Graphs
- Graph Theory - Complement Graphs
- Graph Theory - Graph Products
- Graph Theory - Petersen Graph
- Graph Theory - Cayley Graphs
- Graph Theory - De Bruijn Graphs
- Graph Algorithms
- Graph Theory - Graph Algorithms
- Graph Theory - Breadth-First Search
- Graph Theory - Depth-First Search (DFS)
- Graph Theory - Dijkstra's Algorithm
- Graph Theory - Bellman-Ford Algorithm
- Graph Theory - Floyd-Warshall Algorithm
- Graph Theory - Johnson's Algorithm
- Graph Theory - A* Search Algorithm
- Graph Theory - Kruskal's Algorithm
- Graph Theory - Prim's Algorithm
- Graph Theory - Borůvka's Algorithm
- Graph Theory - Ford-Fulkerson Algorithm
- Graph Theory - Edmonds-Karp Algorithm
- Graph Theory - Push-Relabel Algorithm
- Graph Theory - Dinic's Algorithm
- Graph Theory - Hopcroft-Karp Algorithm
- Graph Theory - Tarjan's Algorithm
- Graph Theory - Kosaraju's Algorithm
- Graph Theory - Karger's Algorithm
- Graph Coloring
- Graph Theory - Coloring
- Graph Theory - Edge Coloring
- Graph Theory - Total Coloring
- Graph Theory - Greedy Coloring
- Graph Theory - Four Color Theorem
- Graph Theory - Coloring Bipartite Graphs
- Graph Theory - List Coloring
- Advanced Topics of Graph Theory
- Graph Theory - Chromatic Number
- Graph Theory - Chromatic Polynomial
- Graph Theory - Graph Labeling
- Graph Theory - Planarity & Kuratowski's Theorem
- Graph Theory - Planarity Testing Algorithms
- Graph Theory - Graph Embedding
- Graph Theory - Graph Minors
- Graph Theory - Isomorphism
- Spectral Graph Theory
- Graph Theory - Graph Laplacians
- Graph Theory - Cheeger's Inequality
- Graph Theory - Graph Clustering
- Graph Theory - Graph Partitioning
- Graph Theory - Tree Decomposition
- Graph Theory - Treewidth
- Graph Theory - Branchwidth
- Graph Theory - Graph Drawings
- Graph Theory - Force-Directed Methods
- Graph Theory - Layered Graph Drawing
- Graph Theory - Orthogonal Graph Drawing
- Graph Theory - Examples
- Computational Complexity of Graph
- Graph Theory - Time Complexity
- Graph Theory - Space Complexity
- Graph Theory - NP-Complete Problems
- Graph Theory - Approximation Algorithms
- Graph Theory - Parallel & Distributed Algorithms
- Graph Theory - Algorithm Optimization
- Graphs in Computer Science
- Graph Theory - Data Structures for Graphs
- Graph Theory - Graph Implementations
- Graph Theory - Graph Databases
- Graph Theory - Query Languages
- Graph Algorithms in Machine Learning
- Graph Neural Networks
- Graph Theory - Link Prediction
- Graph-Based Clustering
- Graph Theory - PageRank Algorithm
- Graph Theory - HITS Algorithm
- Graph Theory - Social Network Analysis
- Graph Theory - Centrality Measures
- Graph Theory - Community Detection
- Graph Theory - Influence Maximization
- Graph Theory - Graph Compression
- Graph Theory Real-World Applications
- Graph Theory - Network Routing
- Graph Theory - Traffic Flow
- Graph Theory - Web Crawling Data Structures
- Graph Theory - Computer Vision
- Graph Theory - Recommendation Systems
- Graph Theory - Biological Networks
- Graph Theory - Social Networks
- Graph Theory - Smart Grids
- Graph Theory - Telecommunications
- Graph Theory - Knowledge Graphs
- Graph Theory - Game Theory
- Graph Theory - Urban Planning
- Graph Theory Useful Resources
- Graph Theory - Quick Guide
- Graph Theory - Useful Resources
- Graph Theory - Discussion
Graph Theory - Connectivity in Dynamic Graphs
Connectivity in Dynamic Graphs
Connectivity in dynamic graphs refers to the way vertices (or nodes) and edges (or lines) evolve over time. A dynamic graph changes as vertices and edges are added or removed, making the connectivity of the graph variable.
The following GIF shows a dynamic graph where nodes are added one by one, followed by edges connecting them sequentially. Later, a node and an edge are removed, and the graph's structure updates visually after each change −

Properties of Dynamic Graphs Connectivity
Connectivity in dynamic graphs has several important properties, including −
- Time-Dependent Connectivity: The connectivity of a dynamic graph can change over time, as edges and vertices are added or removed.
- Instantaneous Connectivity: At any given moment, a dynamic graph can be analyzed for its connectivity, just like static graphs.
- Connectivity Over Time: This property refers to how the graph's connectivity behaves over a period, which may change as vertices and edges are manipulated.
- Dynamic Edge Connectivity: Edge connectivity in a dynamic graph considers how the removal of edges, over time, affects the graph's connectivity.
- Dynamic Vertex Connectivity: This is the minimum number of vertices that need to be removed, over time, to disconnect the graph.
Types of Connectivity in Dynamic Graphs
Connectivity in dynamic graphs can be categorized into different types −
- Dynamic Vertex Connectivity: The minimum number of vertices that need to be removed, over time, to disconnect the remaining graph.
- Dynamic Edge Connectivity: The minimum number of edges that need to be removed, over time, to disconnect the graph.
- Path Connectivity: The ability to find paths between any pair of vertices at a given time, which can be influenced by the dynamic changes in the graph.
- Global Connectivity: This focuses on the overall connectivity of the graph as it evolves over time, considering the cumulative changes.
Dynamic Vertex Connectivity
Dynamic vertex connectivity (t) is the minimum number of vertices that must be removed, at any given time, to disconnect the graph. As vertices are added or removed, this value may change, affecting the graph's overall structure.
- High Dynamic Vertex Connectivity: A high dynamic vertex connectivity indicates that removing multiple vertices is required to disconnect the graph, even over time.
- Low Dynamic Vertex Connectivity: A graph with low dynamic vertex connectivity can be easily disconnected by removing a few vertices during its evolution.
Example
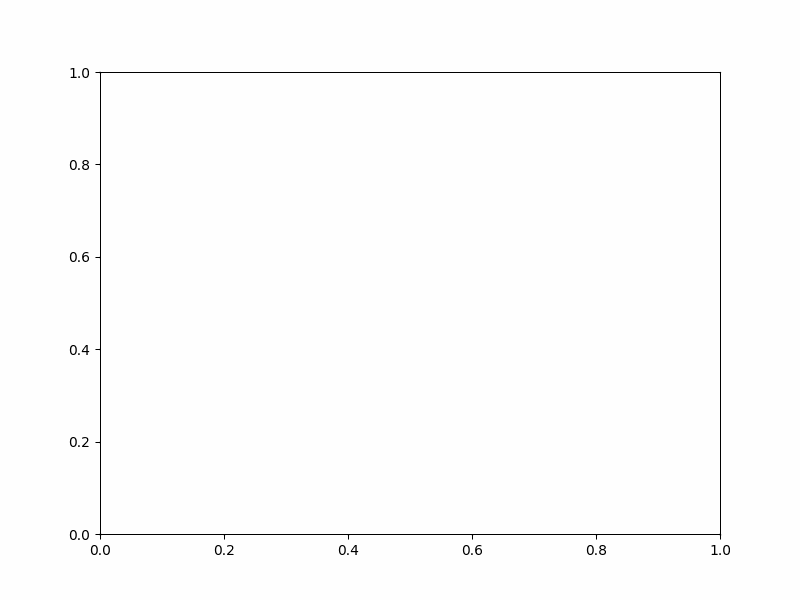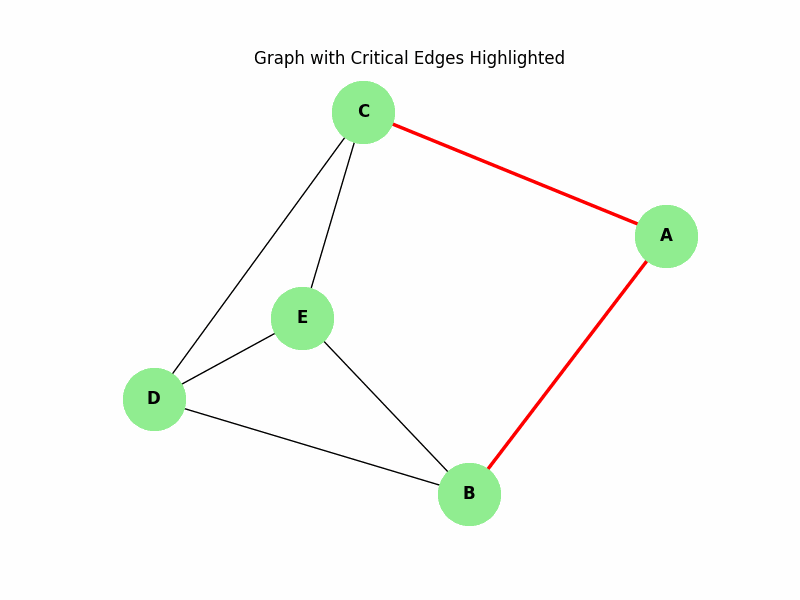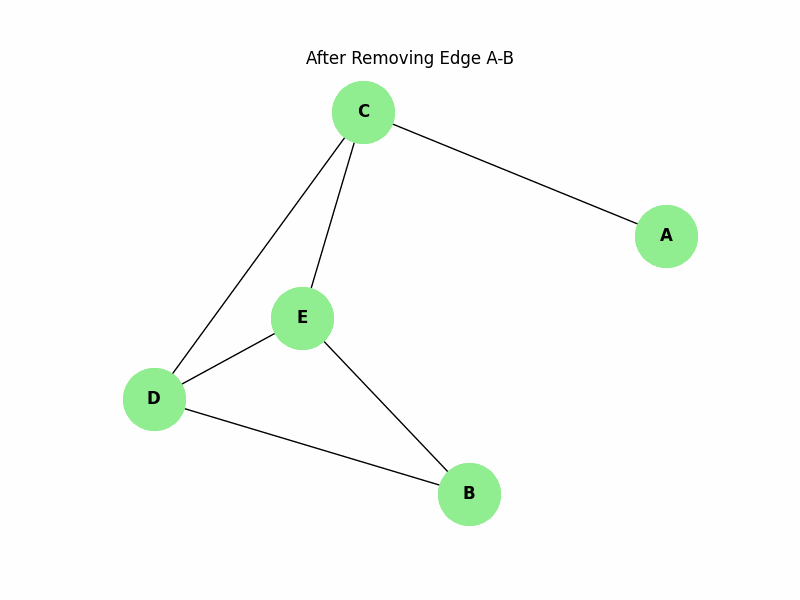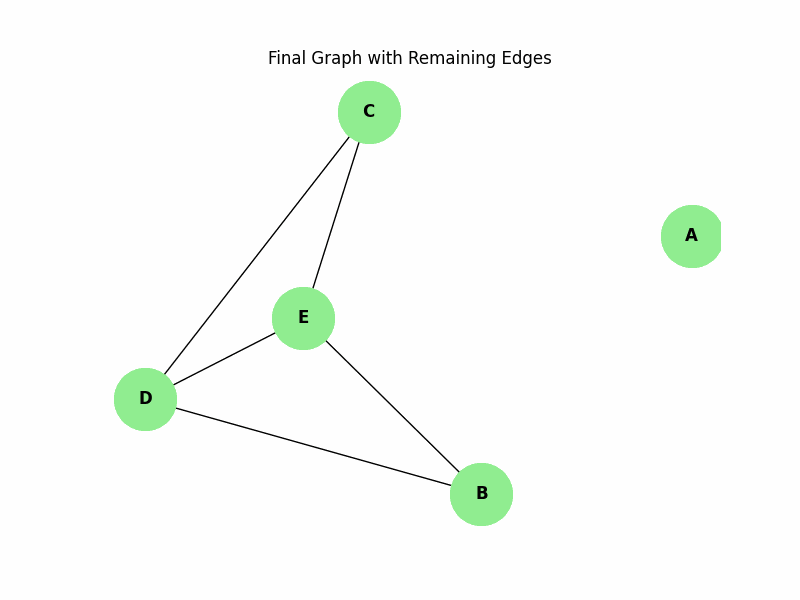
In the following dynamic graph, the removal of vertices A and B disconnects the graph, showing that the dynamic vertex connectivity is 2 −

Dynamic Edge Connectivity
Dynamic edge connectivity (t) is the minimum number of edges that must be removed, over time, to disconnect the graph. Just like dynamic vertex connectivity, this property varies as edges are added or removed.
- High Dynamic Edge Connectivity: A graph with high dynamic edge connectivity remains well-connected even when edges are removed over time.
- Low Dynamic Edge Connectivity: A graph with low dynamic edge connectivity can be easily disconnected by removing a few edges at certain times.
Example
In the following dynamic graph, removing edges (A, B) and (A, C) disconnects the graph, showing that the dynamic edge connectivity is 2 −
Path Connectivity in Dynamic Graphs
Path connectivity in dynamic graphs refers to how easily you can find paths between any two vertices at a given point in time without crossing edges. The connectivity may change as vertices and edges are added or removed from the graph.
- High Path Connectivity: A graph with high path connectivity allows multiple non-crossing paths between any two vertices, even as it evolves.
- Low Path Connectivity: A graph with low path connectivity may have limited paths between vertices that do not cross, making traversal difficult as the graph changes.
Example
In the following dynamic graph, paths can be found between any two vertices without crossing edges, demonstrating good path connectivity over time −
Global Connectivity
Global connectivity in dynamic graphs looks at the overall connectivity of the graph as it changes over time. This property is useful for analyzing the network's performance in real-world applications.
Global connectivity is determined by considering the graph's structure over time and assessing how the removal or addition of vertices and edges impacts its overall connectivity.
- High Global Connectivity: Indicates that even with dynamic changes, the graph remains well-connected across all time points.
- Low Global Connectivity: Suggests that the graph becomes disconnected or weakly connected as it evolves.
Connectivity in Dynamic Graphs Applications
Connectivity in dynamic graphs is applied in various practical scenarios, including −
- Social Networks: Modeling the connections between users as they evolve over time, helping to analyze the stability and growth of networks.
- Communication Networks: Understanding how network topology evolves, ensuring reliable communication even with changing network configurations.
- Transportation Networks: Analyzing connectivity in dynamic transportation networks, where road conditions and routes change over time.
- Routing Algorithms: Dynamic graphs are used in real-time navigation systems to find the best routes as the road network changes.
Testing Connectivity in Dynamic Graphs
Several methods can be used to test connectivity in dynamic graphs, including −
- Dynamic Depth-First Search (DFS): DFS can be adapted to explore the graph dynamically and check connectivity over time.
- Dynamic Breadth-First Search (BFS): BFS can be used to explore the graph level by level, testing connectivity in a dynamic setting.
- Dynamic Connectivity Algorithms: Special algorithms like incremental and decremental algorithms can test how the graph's connectivity evolves as changes occur.
Special Cases of Dynamic Graphs
There are several special types of dynamic graphs with unique connectivity properties, such as −
| Graph Type | Connectivity | Notes |
|---|---|---|
| Social Network Graph | High | Connections between users grow dynamically, leading to high vertex and edge connectivity over time. |
| Transportation Network | Variable | Connectivity can vary depending on changes in roads and traffic patterns over time. |
| Communication Network | Moderate | Connectivity depends on the infrastructure and may change with the addition or removal of components. |
| Mobile Ad-hoc Network | Low | Connectivity can be weak due to the dynamic nature of wireless connections between devices. |
| Dynamic Grid Graph | Variable | Connectivity can change depending on the grid's evolution and additions of edges or vertices. |