Graph Theory - Subgraphs

Quiz

Subgraphs

In graph theory, a subgraph is a graph formed from a subset of the vertices and edges of another graph. Subgraphs plays an important role in understanding the structure and properties of larger graphs by examining their smaller, constituent parts.

Types of Subgraphs

Subgraphs can be categorized based on specific properties and constraints. Here are the main types of subgraphs −

Induced Subgraph

An induced subgraph is formed by selecting a subset of vertices from the original graph and including all the edges that connect pairs of vertices in that subset (edges that exist in the original graph).

The induced subgraph must contain all edges between the selected vertices that are part of the original graph.
No new edges are added; if there is an edge between two selected vertices in the original graph, it will be present in the induced subgraph.

Example

If we have a graph with vertices V = {A, B, C, D} and edges E = {(A-B), (B-C), (C-D), (A-D)}, selecting the vertices {A, B, C} will give the induced subgraph that contains edges {(A-B), (B-C)} (since those are the only edges connecting vertices in {A, B, C} in the original graph) −

Spanning Subgraph

A spanning subgraph contains all the vertices of the original graph but only a subset of its edges. It means that the spanning subgraph includes the complete set of vertices, but it does not necessarily have all the edges that were present in the original graph.

In other words:

Vertices: All vertices of the original graph are retained.
Edges: Some or all of the edges are removed, but the remaining edges still connect the vertices.

Example

If you have a graph with vertices V = {A, B, C, D} and edges E = {(A-B), (B-C), (C-D), (A-D)}, a spanning subgraph can be created by selecting all vertices but only a subset of edges, say E = {(A-B), (B-C)}.

The result will be a graph that still contains all the vertices {A, B, C, D}, but with fewer edges, {(A-B), (B-C)} −

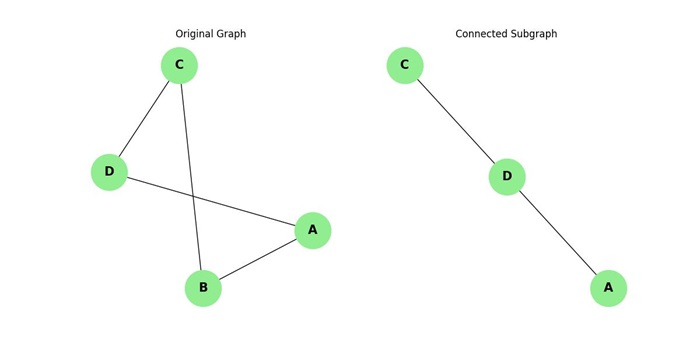
Connected Subgraph

A connected subgraph is any subgraph in which there is a path between every pair of vertices within the subgraph.

A connected subgraph can be any subset of vertices, but the subgraph must be connected meaning, there must be a way to travel between all vertices of the subgraph using the edges in that subgraph.
It may not contain all the edges from the original graph just the ones that maintain connectivity among the selected vertices.

Example

In the same graph with vertices V = {A, B, C, D} and edges E = {(A-B), (B-C), (C-D), (A-D)}, if you choose vertices {A, C, D}, the edges {(A-D), (C-D)} will form a connected subgraph, because there is a path between each pair of vertices in the subset −

Induced Subgraph vs. Spanning Subgraph

The main difference between an induced subgraph and a spanning subgraph is that an induced subgraph can omit vertices but must include all edges between its vertices, whereas a spanning subgraph includes all vertices but can omit edges.

Subgraph Properties

Subgraphs inherit certain properties from their parent graphs. Here are a few important properties −

Vertex and Edge Sets

The vertex set of a subgraph is a subset of the vertex set of the original graph, and the edge set of a subgraph is a subset of the edge set of the original graph.

Degree of Vertices

The degree of a vertex in a subgraph can be different from its degree in the original graph because some edges may be missing in the subgraph.

Connectivity

A connected graph may have disconnected subgraphs. However, a connected subgraph indicates a subset of vertices in which every vertex is reachable from any other vertex in the subgraph.

Paths and Cycles

Paths and cycles in the original graph may or may not exist in its subgraphs, depending on the vertices and edges included in the subgraph.

Finding Subgraphs

There are various methods and algorithms to find subgraphs within a larger graph. Here are some common techniques −

Depth-First Search (DFS)

DFS can be used to explore a graph and identify connected components, which can then be considered as subgraphs. By starting from a vertex and recursively visiting all its adjacent vertices, DFS can identify subgraphs that are connected.

Breadth-First Search (BFS)

Similar to DFS, BFS can also be used to find connected components by exploring the graph level by level. BFS is useful for finding shortest paths and identifying subgraphs in an iterative manner.

Subgraph Isomorphism

Subgraph isomorphism is a problem of finding a subgraph within a larger graph that is isomorphic (structurally identical) to another smaller graph. This is an important problem in areas like pattern recognition and network analysis.

Applications of Subgraphs

Subgraphs plays an important role in various real-world applications, they are −

Social Networks

In social network analysis, subgraphs are used to identify communities or clusters of individuals who are more closely connected to each other than to the rest of the network.

Biological Networks

In biology, subgraphs can represent functional units within larger biological networks, such as protein-protein interaction networks or metabolic pathways.

Computer Networks

In computer networks, subgraphs can be used to model sub-networks or to design and optimize network infrastructure by focusing on important subsets of nodes and connections.

Graph Algorithms

Many graph algorithms, such as those for finding the shortest path, maximum flow, or minimum spanning tree, work by examining and manipulating subgraphs of the original graph.

Example Problems Involving Subgraphs

Let us look at a few example problems that involve subgraphs −

Finding a Spanning Tree

A spanning tree is a subgraph that includes all vertices of the original graph and is a tree (a connected acyclic graph). Algorithms like Kruskal's and Prim's can find spanning trees or minimum spanning trees in weighted graphs.

Detecting Cliques

A clique is a subset of vertices such that every pair of vertices in the subset is connected by an edge. Detecting cliques involves finding subgraphs that are complete.

Identifying Communities

Community detection in graphs involves finding subgraphs where nodes are more densely connected internally than with the rest of the graph. Algorithms like Girvan-Newman and Louvain are used for this purpose.

Graph Partitioning

Graph partitioning involves dividing a graph into disjoint subgraphs such that the number of edges between subgraphs is minimized. This is used in parallel computing and network design.

Algorithms for Subgraph Detection

Several algorithms are specifically designed to detect and analyze subgraphs. Here are a few notable ones:

K-Core Decomposition

K-core decomposition identifies subgraphs where each vertex is connected to at least k other vertices within the subgraph. This helps in identifying densely connected regions.

Motif Finding

Motif finding algorithms detect recurring patterns or subgraphs within a larger graph. These motifs are important in understanding the underlying structure of the graph.

Frequent Subgraph Mining

Frequent subgraph mining algorithms, like gSpan, find subgraphs that frequently appear in a collection of graphs. This is useful in areas like chemical informatics and social network analysis.

Print Page