Graph Theory - Graph Partitioning

---

---

Graph Partitioning

Graph Partitioning is a process of dividing a graph into multiple smaller, disconnected subgraphs while minimizing the number of edges between them. The main goal is to ensure that the partitions or subgraphs are balanced in terms of size or weight, and that the cuts (edges between partitions) are minimized.

The above diagram visualizes the process of graph partitioning where a large graph is split into smaller clusters or subgraphs.

Partition 1: [0, 4, 5, 7]
Partition 2: [1, 2, 3, 6]

Properties of Graph Partitioning

Following are the major properties of graph partitioning −

• Minimization of Edge Cuts: The objective is to minimize the number of edges between the partitions or subgraphs, also known as the "cut" between the partitions.
• Balanced Partition Sizes: Each partition should have a similar number of nodes, which ensures fairness in the division and avoids large partitions that might cause load imbalance.
• Weight Balance: If the graph has weighted edges, the partitioning should aim to balance the total weight of edges within each partition.

Types of Graph Partitioning

There are various types of graph partitioning techniques, each with different types of graphs and optimization goals. The main types ar as follows −

• Balanced Partitioning
• Multilevel Partitioning
• Spectral Partitioning
• Geometric Partitioning

Balanced Partitioning

Balanced Partitioning is used to divide a graph or a set of elements into two or more parts such that each part has an approximately equal number of elements or is balanced in terms of certain criteria (such as weight).

The goal is to achieve an equitable distribution of data while maintaining a minimal number of connections (or edges) between the parts. In graph theory, this technique is particularly useful for dividing a graph into subgraphs that minimize the cut size the number of edges connecting different partitions.

Example

For a graph with 10 nodes, the following steps are applied −

• Start with the original graph of 12 nodes.
• Apply a partitioning algorithm to divide the graph into two equal parts, each containing 6 nodes.
• Optimize the cut between the two partitions to minimize the number of edges connecting the two parts, ensuring the partitions are balanced in terms of both size and edge cuts.
• If needed, refine the partitions by applying further adjustments, ensuring each partition is balanced while minimizing the connection between them.

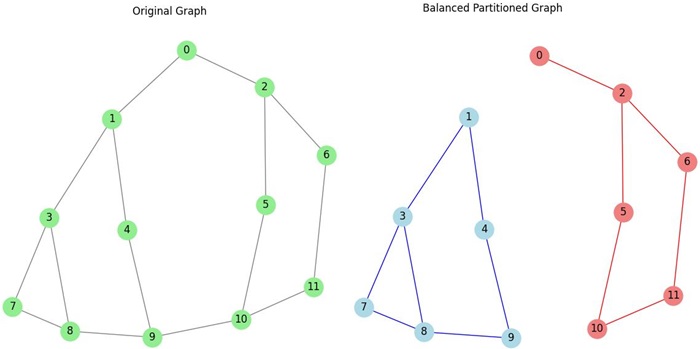
Partition 1: [1, 3, 4, 7, 8, 9]
Partition 2: [0, 2, 5, 6, 10, 11]

Multilevel Partitioning

Multilevel Partitioning is used to divide a larger graph into smaller subgraphs or partitions. It works by coarsening the graph, partitioning it at a smaller scale, and then uncoarsing it back to its original size while refining the partition. Here is how it works −

• Coarsing: The original graph is iteratively reduced into smaller, more manageable graphs by collapsing vertices and edges. This results in a graph with fewer nodes and edges, making the partitioning process easier.
• Initial Partitioning: After coarsing, a partitioning algorithm is applied to the smaller graph. The goal is to divide the graph into separate partitions or clusters while minimizing the edge cuts between them.
• Uncoarsing: The coarsed graph is expanded back to the original graph by restoring the collapsed nodes and edges. As this happens, the partitions are refined, and adjustments are made to optimize the cuts between the partitions.
• Refinement: In this step, additional refinement is applied to the partition to minimize edge cuts and improve the balance of the partitions, ensuring that they are as equal as possible in terms of both size and connectivity.

Example

For a graph with 10 nodes, the following steps are applied −

• Start with the original graph and coarsen it into a smaller graph with 5 nodes.
• Apply an initial partitioning on the 5-node graph.
• Uncoarse the 5-node graph back to the original 10-node graph, and refine the partitions by optimizing the edge cuts.

Spectral Graph Partitioning

Spectral Graph Partitioning uses the eigenvalues and eigenvectors of the Laplacian matrix of a graph to partition it into clusters. This method is based on the principle that the eigenvectors of the Laplacian matrix can reveal the inherent divisions or clusters within the graph, helping to organize the graph into meaningful subsets.

In spectral partitioning, the Laplacian matrix L of a graph is computed as −

L = D - A

Where D is the degree matrix (a diagonal matrix with the degrees of the nodes) and A is the adjacency matrix of the graph.

Once the Laplacian matrix is computed, the eigenvectors corresponding to the smallest eigenvalues are found. These eigenvectors are then used to partition the graph into two or more clusters, based on their components.

Example

Consider a graph with the following adjacency matrix −

Adjacency Matrix A:
[[0, 1, 1, 0, 0],
 [1, 0, 1, 1, 0],
 [1, 1, 0, 0, 0],
 [0, 1, 0, 0, 1],
 [0, 0, 0, 1, 0]]

The Laplacian matrix L is computed, and its eigenvectors are used to divide the graph into two clusters:

• Cluster 1: Nodes {0, 1, 2}
• Cluster 2: Nodes {3, 4}

Cluster 1: Nodes [0, 1, 2]
Cluster 2: Nodes [3, 4]

Geometric Partitioning

Geometric Partitioning is used for dividing a graph or a set of data into smaller parts based on their geometric properties. The main idea is to partition the graph according to spatial or geometric features, often using coordinates or distances to guide the separation of the graph into regions.

In geometric partitioning,

• The nodes (vertices) of the graph represent points in a geometric space.
• The goal is to divide the graph into clusters or partitions in such a way that the edges between the partitions are minimized while maintaining the overall structure of the graph.
• Common methods for geometric partitioning include algorithms like k-means clustering or Voronoi diagrams, where the graph is partitioned based on distances, angles, or other spatial criteria.

Graph Partitioning Algorithms

We can use various algorithms to partition graphs, such as −

• Kernighan-Lin Algorithm: This algorithm improves graph partitions by swapping nodes between two groups to reduce the number of edges connecting them.
• Metis Algorithm: A multilevel algorithm that uses refinement techniques to partition large graphs. It is majorly used in parallel computing.
• Normalized Cut Algorithm: This technique splits the graph by minimizing the ratio of the edge cuts to the total connections of the groups, helping to create balanced partitions.
• Fiduccia-Mattheyses Algorithm: A practical approach for balancing partition sizes while reducing edge cuts, often used in designing circuits.

Example: Kernighan-Lin Algorithm

For a simple graph, the Kernighan-Lin algorithm starts by randomly assigning nodes to two partitions. It then iteratively swaps nodes between partitions to reduce the number of edges between them. The algorithm stops when no further improvement is possible.