Graph Theory - k-Connected Graphs

---

---

k-Connected Graphs

k-connected graphs, also known as k-vertex-connected graphs, are graphs that remain connected even after the removal of up to k-1 vertices. In other words, a graph is k-connected if it takes removing at least k vertices to disconnect the graph.

• If a graph is disconnected, its connectivity is 0 because it is already not connected.
• If a graph is 1-connected, removing any single vertex does not disconnect the graph.
• If a graph is k-connected (k > 1), it requires the removal of at least k vertices to disconnect the graph.
• The higher the value of k, the more strong the graph is against vertex removals.

The vertex connectivity of a graph G, denoted by (G), is the largest integer k for which the graph is k-connected.

Calculating k-Connectivity

To calculate k-connectivity, we follow these steps −

• Identify all subsets of vertices whose removal disconnects the graph.
• Find the smallest subset of vertices that disconnects the graph.
• The size of this smallest subset is the vertex connectivity.

Consider the following graph −

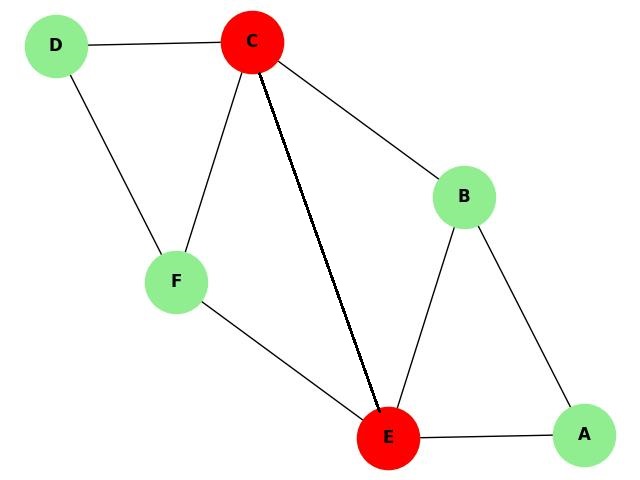
In this graph, if we remove vertices C and E, the graph becomes disconnected. Therefore, the vertex connectivity is 2, as removing two vertices disconnects the graph.

Properties of k-Connected Graphs

k-connected graphs have several important properties, such as −

• Non-negative: The vertex connectivity of any graph is always non-negative.
• Lower Bound: The vertex connectivity of a connected graph is at least 1. For a disconnected graph, the vertex connectivity is 0.
• Upper Bound: The vertex connectivity of a graph is at most n-1, where n is the number of vertices in the graph.
• Complete Graphs: For complete graphs, the vertex connectivity is n-1, as removing n-1 vertices disconnects the graph.

2-Connected Graph

A 2-connected graph remains connected even after the removal of any one vertex. Removing any two vertices is required to disconnect the graph.

In the above given graph, removing any single vertex does not disconnect the graph, but removing two vertices (e.g., C and E) will disconnect the graph.

3-Connected Graph

A 3-connected graph remains connected even after the removal of any two vertices. Removing any three vertices is required to disconnect the graph.

The following image displays a 3-connected graph:

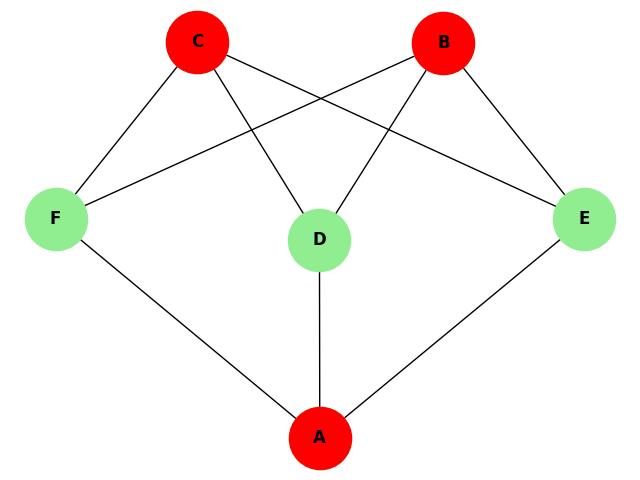
In this graph, removing any two vertices does not disconnect the graph, but removing three vertices (e.g., A, B, and C) will disconnect the graph.

Applications of k-Connected Graphs

k-connected graphs have various applications, such as −

• Network Design: In designing strong communication networks, higher vertex connectivity ensures that the network remains operational even if multiple nodes fail.
• Fault Tolerance: k-connected graphs help in designing fault-tolerant systems where the failure of up to k-1 components does not disrupt the overall system.
• Graph Theory Research: k-connected graphs are a fundamental concept in graph theory and are used in various theoretical research areas.
• Routing and Navigation: In transportation and routing networks, k-connected graphs ensure multiple alternative routes, enhancing reliability and efficiency.

For instance, in a transportation network, higher vertex connectivity ensures that the failure of up to k-1 intersections does not cause a breakdown in the transportation system.

Theorems Related to k-Connected Graphs

There are various important theorems related to k-connected graphs that help us to understand their properties and applications. The two major theorems are −

• Menger's Theorem
• Whitney's Theorem

Menger's Theorem

Menger's Theorem provides a relationship between vertex connectivity and paths in a graph. It states that the minimum number of vertices that need to be removed to disconnect two non-adjacent vertices is equal to the maximum number of independent paths between those vertices.

Example of Menger's Theorem

Consider a graph where there are two independent paths between vertices A and B. These paths do not share any common vertices except for A and B.

According to Menger's Theorem, at least two vertices must be removed to disconnect A from B. This is because the number of independent paths between A and B (2) directly corresponds to the minimum number of vertices required to disconnect the two vertices.

Removing fewer than two vertices will not disconnect A and B, as there will still be paths connecting them.

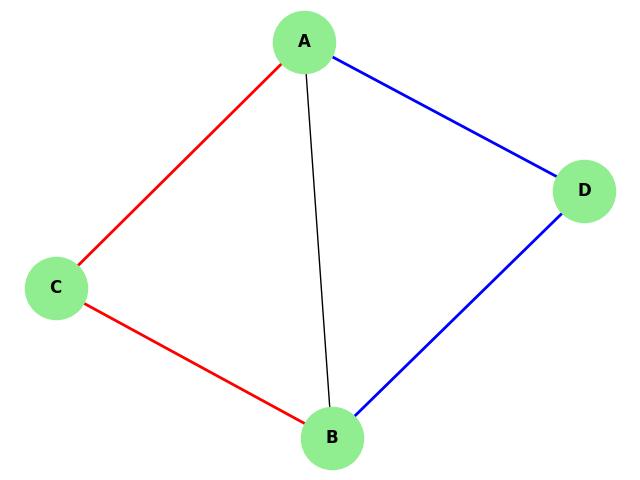
Independent paths between A and B:
['A', 'C', 'B']
['A', 'D', 'B']

Whitney's Theorem

Whitney's Theorem provides a characterization of k-connected graphs. It states that a graph is k-connected if and only if it has at least k+1 vertices and the removal of any set of fewer than k vertices leaves the remaining subgraph connected.

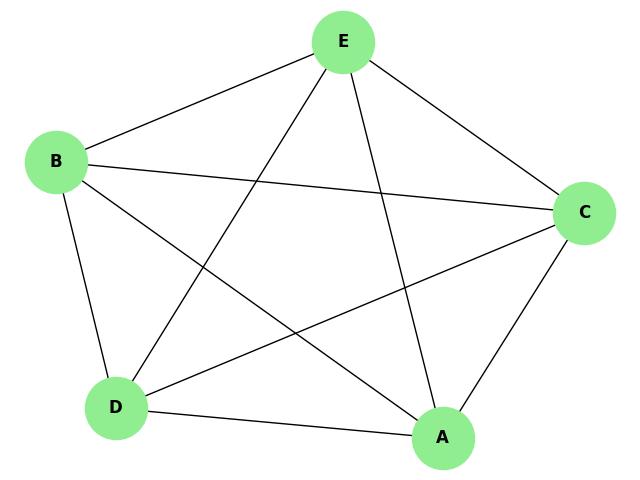
Example of Whitney's Theorem

Consider a graph with five vertices and the removal of any two vertices does not disconnect the graph. According to Whitney's Theorem, this graph is 3-connected because it satisfies the condition that removing fewer than three vertices keeps the graph connected.

Therefore, the vertex connectivity of this graph is 3, indicating its robustness against vertex removals.

Special Cases of k-Connected Graphs

There are several special cases of k-connected graphs, including −

• 1-Connected Graphs: Also known as simply connected or connected graphs, they remain connected with the removal of any single vertex.
• 2-Connected Graphs: Also known as biconnected graphs, they remain connected with the removal of any two vertices.
• 3-Connected Graphs: Also known as triconnected graphs, they remain connected with the removal of any three vertices.

Each of these special cases represents a higher level of connectivity and robustness in the graph structure.

Example of a 1-Connected Graph

A 1-connected graph remains connected even after the removal of any single vertex. Removing any one vertex is required to disconnect the graph.

The following image displays a 1-connected graph −

In this graph, removing any single vertex does not disconnect the graph, but removing one vertex will disconnect the graph.