Graph Theory - Vertex Connectivity

---

---

Vertex Connectivity of a Graph

Vertex connectivity of a graph refers to the minimum number of vertices that need to be removed to disconnect the graph or make it disconnected.

• If a graph is disconnected, its vertex connectivity is defined as 0 because removing any number of vertices will leave it disconnected.
• If a graph is connected, the vertex connectivity is at least 1 because removing no vertices will leave it connected.
• The higher the vertex connectivity, the more strong the graph is against the removal of vertices.

The vertex connectivity of a graph G, denoted by (G), is the smallest number of vertices that must be removed from the graph to either −

• Disconnect the graph (split it into two or more disconnected components).
• Make the graph trivial (a single vertex or no vertices at all).

Calculating Vertex Connectivity

To calculate the vertex connectivity, we follow these steps −

• Identify all subsets of vertices whose removal disconnects the graph.
• Find the smallest subset of vertices that disconnects the graph.
• The size of this smallest subset is the vertex connectivity.

Consider the following graph:

In this graph, if we remove vertex A, the graph becomes disconnected, with vertices C and F being separated from the rest. Therefore, the vertex connectivity is 1, as removing a single vertex disconnects the graph.

Properties of Vertex Connectivity

The vertex connectivity of a graph has several important properties, such as −

• Non-negative: The vertex connectivity of any graph is always non-negative.
• Lower Bound: The vertex connectivity of a graph is at least 1 for a connected graph. In the case of a disconnected graph, the vertex connectivity is 0.
• Upper Bound: The vertex connectivity of a graph is at most n-1, where n is the number of vertices in the graph.
• Graph Completeness: For complete graphs, the vertex connectivity is n-1, as removing n-1 vertices disconnects the graph.

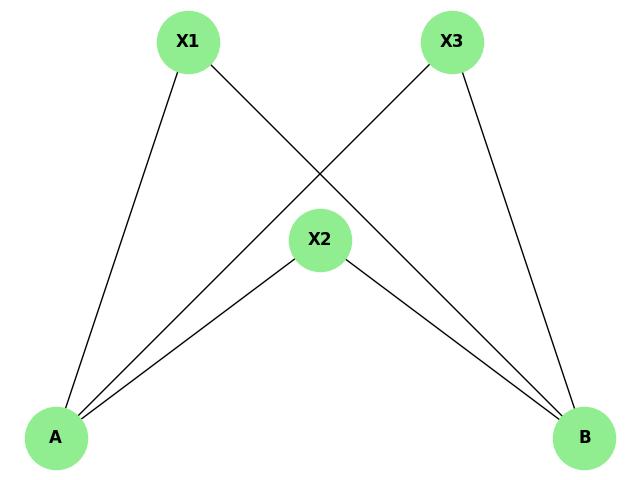
Star Graph Vertex Connectivity

The star graph has a central vertex connected to all other vertices, and removing the central vertex disconnects the graph. Hence, the vertex connectivity of a star graph is 1.

The following image displays a star graph with vertex connectivity of 1 −

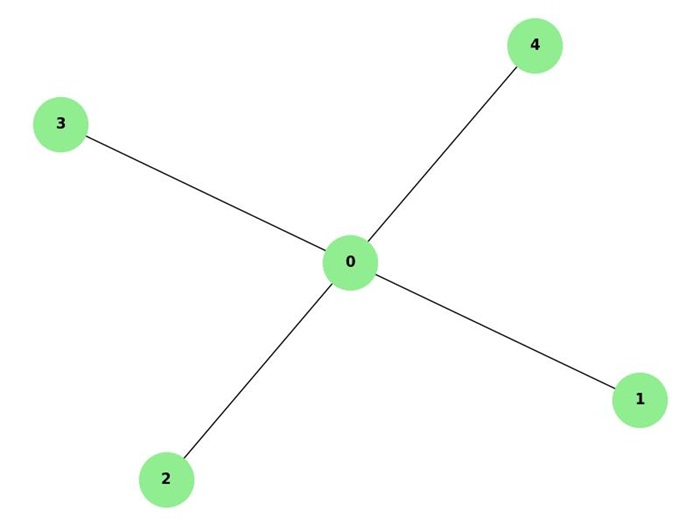
Complete Graph Vertex Connectivity

A complete graph has an edge between every pair of vertices. Since the graph is fully connected, removing any vertex still keeps the graph connected. Therefore, the vertex connectivity of a complete graph with 5 vertices is 4 (one less than the total number of vertices).

The following image displays a complete graph with vertex connectivity of 4 −

Types of Vertex Connectivity

There are two main types of vertex connectivity, they are −

• Global Vertex Connectivity
• Local Vertex Connectivity

Global Vertex Connectivity

Global Vertex Connectivity refers to the overall connectivity of the graph. It is defined as the smallest number of vertices that must be removed to disconnect the entire graph into at least two disconnected subgraphs.

In other words, it measures how strong the graph is against the removal of vertices. A graph with higher global vertex connectivity is more resistant to disconnection.

Example of Global Vertex Connectivity

Consider a complete graph with four vertices, labeled A, B, C, and D, where every vertex is connected to every other vertex. In this case, removing any two vertices from the graph would disconnect the graph, as the remaining two vertices would no longer be connected to each other.

Therefore, the global vertex connectivity of this graph is 2, as removing two vertices is the minimum number required to disconnect the entire graph.

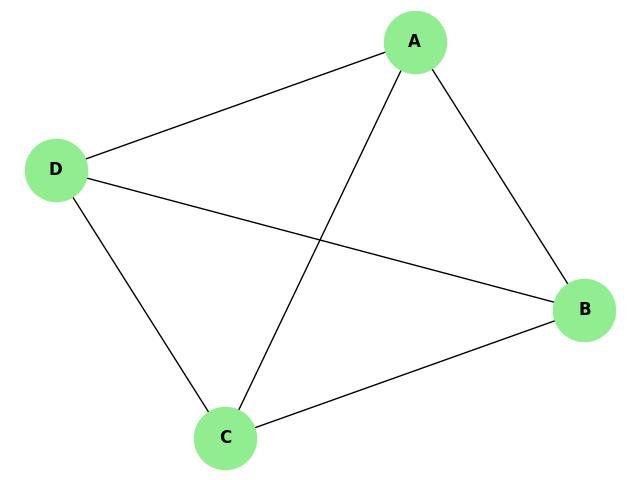
• Graph: A - B - C - D (with edges between every pair of vertices)
• Global Connectivity: 2 (removing two vertices disconnects the graph)

Local Vertex Connectivity

Local Vertex Connectivity refers to the connectivity around a particular vertex in the graph. It is defined as the minimum number of vertices that must be removed to disconnect that specific vertex from the rest of the graph. Local connectivity measures how critical a vertex is to the overall connectivity of the graph.

Example of Local Vertex Connectivity

Consider a star graph with five vertices: one central vertex (A) and four outer vertices (B, C, D, E) connected only to the central vertex.

In this case, removing any one of the outer vertices (B, C, D, or E) does not disconnect the central vertex from the rest of the graph. However, removing the central vertex (A) will disconnect the entire graph, as the outer vertices will no longer be connected.

Therefore, the local vertex connectivity for any outer vertex (B, C, D, or E) is 1, as removing just one vertex is enough to disconnect that specific outer vertex from the graph.

• Graph: A (center) connected to B, C, D, E (outer vertices)
• Local Connectivity (for any outer vertex): 1 (removing one outer vertex does not disconnect A)

Applications of Vertex Connectivity

Vertex connectivity plays an important role in many applications, such as −

• Network Robustness: In computer networks, vertex connectivity shows how strong the network is against node failures. A higher vertex connectivity means the network is less likely to be disconnected if some nodes fail.
• Graph Partitioning: In dividing large networks or graphs into smaller subgraphs, vertex connectivity helps in ensuring that the partition does not disconnect parts of the graph.
• Communication Networks: Vertex connectivity is important for designing communication networks, where the objective is to ensure that a network remains connected despite the failure of certain nodes or vertices.
• Fault Tolerance: A graph with high vertex connectivity can handle node failures without losing its connectivity, making the network more reliable and efficient.

For instance, in a communication network, each node represents a communication device. If one device fails, the network's connectivity is impacted. Higher vertex connectivity ensures that the failure of one device does not cause a breakdown in the communication between other devices.

Theorems in Vertex Connectivity

There are several important theorems related to vertex connectivity. These theorems help us understand the relationship between vertex and edge connectivity and provide useful methods for analyzing graphs. Two important theorems are −

• Knig's Theorem
• Menger's Theorem

Knig's Theorem

Knig's Theorem states that in a connected graph, the vertex connectivity is equal to the edge connectivity of the graph.

Edge connectivity refers to the minimum number of edges that need to be removed to disconnect the graph, while vertex connectivity refers to the minimum number of vertices that need to be removed to achieve the same result. According to this theorem, these two quantities are equal in a connected graph.

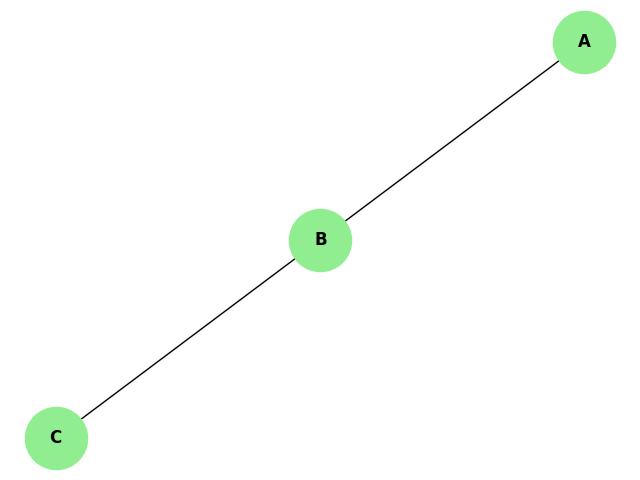
Example of Knig's Theorem

Consider a simple graph where vertices A, B, and C are connected by edges. If we remove one vertex (say, vertex B), the graph will be disconnected, as A will no longer be connected to C.

In this case, removing one vertex results in disconnection, so the vertex connectivity is 1. Similarly, if we remove the edge connecting A to B or the edge connecting B to C, the graph will also become disconnected.

Thus, the edge connectivity is also 1. According to Knig's Theorem, the vertex connectivity (1) is equal to the edge connectivity (1).

Menger's Theorem

Menger's Theorem provides a more general view of vertex connectivity, stating that the minimum number of vertices that need to be removed to disconnect a graph is equal to the maximum number of vertex-disjoint paths between any two vertices in the graph.

Vertex-disjoint paths are paths that do not share any common vertices except for the start and end vertices.

Example of Menger's Theorem

Consider a graph where there are three vertex-disjoint paths between two vertices, A and B. These paths do not share any common vertex except for A and B.

According to Menger's Theorem, at least three vertices must be removed from the graph to disconnect A from B. This is because the number of vertex-disjoint paths between A and B (3) directly corresponds to the minimum number of vertices required to disconnect the two vertices.

Removing fewer than three vertices will not disconnect A and B, as there will still be paths connecting them.