Graph Theory - List Coloring

---

---

List Coloring in Graph Theory

List coloring is a variation of the graph coloring problem where each vertex in a graph has its own list of permissible colors.

In list coloring, permissible colors refer to the specific set of colors that are allowed to be assigned to a vertex in a graph.

Unlike standard graph coloring, where any color from a fixed set can be used, in list coloring, each vertex has its own list of permissible colors, which can vary from vertex to vertex.

The goal is to assign a color to each vertex from its respective list, ensuring that adjacent vertices have different colors.

• The assigned color for each vertex comes from its list of permissible colors.
• No two adjacent vertices share the same color.

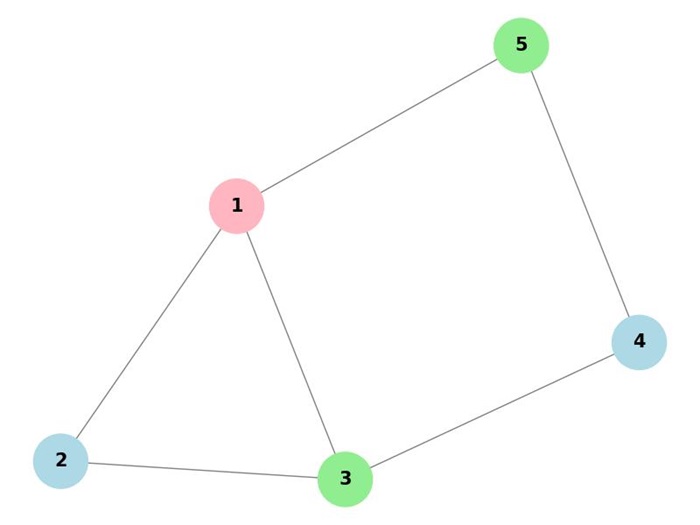
Here,

Lists of permissible colors for each vertex:
Vertex 1: ['lightpink', 'lightblue']
Vertex 2: ['lightblue', 'lightgreen']
Vertex 3: ['lightpink', 'lightgreen']
Vertex 4: ['lightblue', 'yellow']
Vertex 5: ['lightgreen', 'yellow']

Color assignment: {1: 'lightpink', 2: 'lightblue', 3: 'lightgreen', 4: 'lightblue', 5: 'lightgreen'}

A graph is said to be list colorable if such an assignment exists for any collection of lists of allowable colors, as long as the size of each list is at least a certain value, called the list chromatic number of the graph.

List Chromatic Number

The list chromatic number of a graph is the smallest number k such that for any assignment of lists of size k to the vertices, the graph can be properly colored using the lists. It is denoted as X₁(G), where G is the graph.

In simple terms, the list chromatic number defines the minimum size of the color list required for each vertex so that a valid coloring exists, where no two adjacent vertices share the same color, regardless of the specific colors in the lists.

For many graphs, the list chromatic number is equal to the chromatic number, but this is not always the case. Determining the list chromatic number can be more complex than finding the chromatic number.

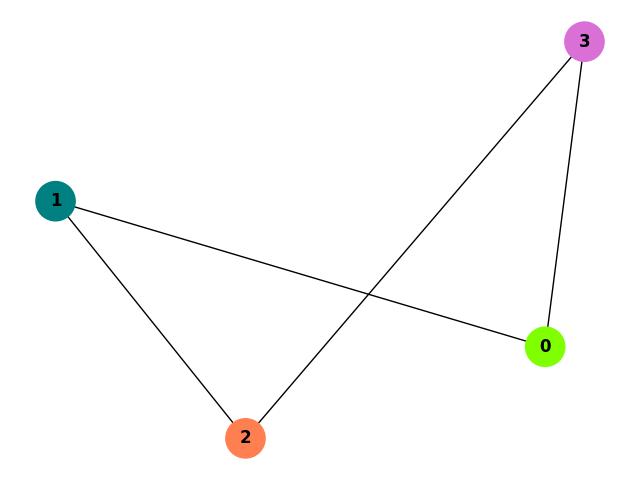
Here,

Permissible color lists for each vertex:
Node 0: ['Chartreuse', 'teal', 'coral']
Node 1: ['Chartreuse', 'teal', 'coral']
Node 2: ['teal', 'coral', 'Orchid']
Node 3: ['Chartreuse', 'coral', 'Orchid']

The graph is list colorable with the given lists. Coloring:
Node 0: Chartreuse
Node 1: teal
Node 2: coral
Node 3: Orchid

The List Chromatic Number of the graph is: 3

The list chromatic number of the above graph is 3.

Properties of List Coloring

List coloring has various interesting properties that differentiate it from traditional graph coloring −

• Generalization: Every graph that is k-colorable is also list colorable with lists of size k, but the reverse is not necessarily true.
• Dependence on Lists: The feasibility of a proper list coloring depends on the specific lists of allowable colors assigned to the vertices.
• Flexibility: List coloring is more flexible in assigning colors when constraints exist on individual vertices.

Applications of List Coloring

List coloring has various applications in real-world scenarios, particularly in areas where constraints must be considered −

• Scheduling: In scheduling problems, tasks may have restrictions on which time slots or resources they can use. These restrictions can be modeled as lists of permissible options for each task, which must be assigned without conflicts.
• Frequency Assignment: In wireless networks, frequencies must be assigned to transmitters in such a way that interference is minimized. Each transmitter may have a restricted list of frequencies it can use, which can be represented through list coloring to avoid conflicts.
• Resource Allocation: In resource allocation problems, where resources are limited or certain resources are restricted for specific entities, list coloring ensures that each entity is assigned the most suitable and non-conflicting resources from its allowable list.
• Graph Labeling: In labeling problems, vertices may have constraints on the labels they can receive. List coloring provides a way to assign valid labels to vertices, ensuring that the constraints are met.

Algorithm for List Coloring

Finding a valid list coloring for a graph can be a challenging task. However, several algorithms and techniques have been developed to handle specific cases −

• Backtracking: A backtracking approach can be used to try different color assignments for each vertex from its permissible list. It checks for conflicts at each step and backtracks when necessary to find a valid coloring.
• Greedy Algorithm: A greedy algorithm can sometimes produce a solution if the color lists are large enough. However, it does not guarantee a solution for all types of graphs.
• Special Graph Classes: For certain graph classes, such as bipartite or planar graphs, there are more efficient algorithms that can be used for list coloring.

Despite these techniques, list coloring remains an NP-hard problem in the general case.

To better understand list coloring, consider the following examples −

Simple Graph with Lists

Suppose we have a graph with three vertices (A, B, C) and edges (A-B, B-C). Each vertex has the following list of permissible colors:

• A: {Red, Blue}
• B: {Green, Red}
• C: {Blue, Green}

A valid list coloring would be:

• A: Red
• B: Green
• C: Blue

Each vertex is assigned a color from its list, and no two adjacent vertices share the same color.

Constraints on Coloring

Consider a triangle graph (A-B-C-A) with the following lists:

• A: {Red, Green}
• B: {Green, Blue}
• C: {Red, Blue}

A valid coloring is not possible in this case, as no assignment satisfies both the adjacency condition and the constraints imposed by the lists.

Challenges in List Coloring

List coloring poses unique challenges compared to traditional graph coloring:

• Increased Complexity: The presence of individual lists for each vertex increases the complexity of finding a proper coloring.
• No Universal Algorithm: There is no single algorithm that guarantees a solution for all graphs and list assignments.
• Dependence on List Sizes: The feasibility of a list coloring depends on the size and content of the lists, which may vary between vertices.

Despite these challenges, list coloring remains an important and useful tool for solving graph coloring problems with specific constraints.