
- Graph Theory - Home
- Graph Theory - Introduction
- Graph Theory - History
- Graph Theory - Fundamentals
- Graph Theory - Applications
- Types of Graphs
- Graph Theory - Types of Graphs
- Graph Theory - Simple Graphs
- Graph Theory - Multi-graphs
- Graph Theory - Directed Graphs
- Graph Theory - Weighted Graphs
- Graph Theory - Bipartite Graphs
- Graph Theory - Complete Graphs
- Graph Theory - Subgraphs
- Graph Theory - Trees
- Graph Theory - Forests
- Graph Theory - Planar Graphs
- Graph Theory - Hypergraphs
- Graph Theory - Infinite Graphs
- Graph Theory - Random Graphs
- Graph Representation
- Graph Theory - Graph Representation
- Graph Theory - Adjacency Matrix
- Graph Theory - Adjacency List
- Graph Theory - Incidence Matrix
- Graph Theory - Edge List
- Graph Theory - Compact Representation
- Graph Theory - Incidence Structure
- Graph Theory - Matrix-Tree Theorem
- Graph Properties
- Graph Theory - Basic Properties
- Graph Theory - Coverings
- Graph Theory - Matchings
- Graph Theory - Independent Sets
- Graph Theory - Traversability
- Graph Theory Connectivity
- Graph Theory - Connectivity
- Graph Theory - Vertex Connectivity
- Graph Theory - Edge Connectivity
- Graph Theory - k-Connected Graphs
- Graph Theory - 2-Vertex-Connected Graphs
- Graph Theory - 2-Edge-Connected Graphs
- Graph Theory - Strongly Connected Graphs
- Graph Theory - Weakly Connected Graphs
- Graph Theory - Connectivity in Planar Graphs
- Graph Theory - Connectivity in Dynamic Graphs
- Special Graphs
- Graph Theory - Regular Graphs
- Graph Theory - Complete Bipartite Graphs
- Graph Theory - Chordal Graphs
- Graph Theory - Line Graphs
- Graph Theory - Complement Graphs
- Graph Theory - Graph Products
- Graph Theory - Petersen Graph
- Graph Theory - Cayley Graphs
- Graph Theory - De Bruijn Graphs
- Graph Algorithms
- Graph Theory - Graph Algorithms
- Graph Theory - Breadth-First Search
- Graph Theory - Depth-First Search (DFS)
- Graph Theory - Dijkstra's Algorithm
- Graph Theory - Bellman-Ford Algorithm
- Graph Theory - Floyd-Warshall Algorithm
- Graph Theory - Johnson's Algorithm
- Graph Theory - A* Search Algorithm
- Graph Theory - Kruskal's Algorithm
- Graph Theory - Prim's Algorithm
- Graph Theory - Borůvka's Algorithm
- Graph Theory - Ford-Fulkerson Algorithm
- Graph Theory - Edmonds-Karp Algorithm
- Graph Theory - Push-Relabel Algorithm
- Graph Theory - Dinic's Algorithm
- Graph Theory - Hopcroft-Karp Algorithm
- Graph Theory - Tarjan's Algorithm
- Graph Theory - Kosaraju's Algorithm
- Graph Theory - Karger's Algorithm
- Graph Coloring
- Graph Theory - Coloring
- Graph Theory - Edge Coloring
- Graph Theory - Total Coloring
- Graph Theory - Greedy Coloring
- Graph Theory - Four Color Theorem
- Graph Theory - Coloring Bipartite Graphs
- Graph Theory - List Coloring
- Advanced Topics of Graph Theory
- Graph Theory - Chromatic Number
- Graph Theory - Chromatic Polynomial
- Graph Theory - Graph Labeling
- Graph Theory - Planarity & Kuratowski's Theorem
- Graph Theory - Planarity Testing Algorithms
- Graph Theory - Graph Embedding
- Graph Theory - Graph Minors
- Graph Theory - Isomorphism
- Spectral Graph Theory
- Graph Theory - Graph Laplacians
- Graph Theory - Cheeger's Inequality
- Graph Theory - Graph Clustering
- Graph Theory - Graph Partitioning
- Graph Theory - Tree Decomposition
- Graph Theory - Treewidth
- Graph Theory - Branchwidth
- Graph Theory - Graph Drawings
- Graph Theory - Force-Directed Methods
- Graph Theory - Layered Graph Drawing
- Graph Theory - Orthogonal Graph Drawing
- Graph Theory - Examples
- Computational Complexity of Graph
- Graph Theory - Time Complexity
- Graph Theory - Space Complexity
- Graph Theory - NP-Complete Problems
- Graph Theory - Approximation Algorithms
- Graph Theory - Parallel & Distributed Algorithms
- Graph Theory - Algorithm Optimization
- Graphs in Computer Science
- Graph Theory - Data Structures for Graphs
- Graph Theory - Graph Implementations
- Graph Theory - Graph Databases
- Graph Theory - Query Languages
- Graph Algorithms in Machine Learning
- Graph Neural Networks
- Graph Theory - Link Prediction
- Graph-Based Clustering
- Graph Theory - PageRank Algorithm
- Graph Theory - HITS Algorithm
- Graph Theory - Social Network Analysis
- Graph Theory - Centrality Measures
- Graph Theory - Community Detection
- Graph Theory - Influence Maximization
- Graph Theory - Graph Compression
- Graph Theory Real-World Applications
- Graph Theory - Network Routing
- Graph Theory - Traffic Flow
- Graph Theory - Web Crawling Data Structures
- Graph Theory - Computer Vision
- Graph Theory - Recommendation Systems
- Graph Theory - Biological Networks
- Graph Theory - Social Networks
- Graph Theory - Smart Grids
- Graph Theory - Telecommunications
- Graph Theory - Knowledge Graphs
- Graph Theory - Game Theory
- Graph Theory - Urban Planning
- Graph Theory Useful Resources
- Graph Theory - Quick Guide
- Graph Theory - Useful Resources
- Graph Theory - Discussion
Graph Theory - Examples
Graph Theory is a fundamental branch of mathematics and computer science that focuses on studying graphs. Graphs are used to represent connections between objects, with points called vertices (or nodes) linked by lines called edges.
In this tutorial, we will look at different real-world and theoretical examples of graphs. Each example will show how graphs are used in various fields, making it easier to understand how graph theory helps solve problems.
Examples of Undirected Graphs
An undirected graph is a type of graph in which edges have no direction, meaning the connections between nodes are bidirectional. Let us examine examples of undirected graphs to understand their properties.
Example: Social Network
Consider a social network where people are represented as nodes, and friendships between them are represented as edges. If two people are friends, they are connected by an undirected edge.
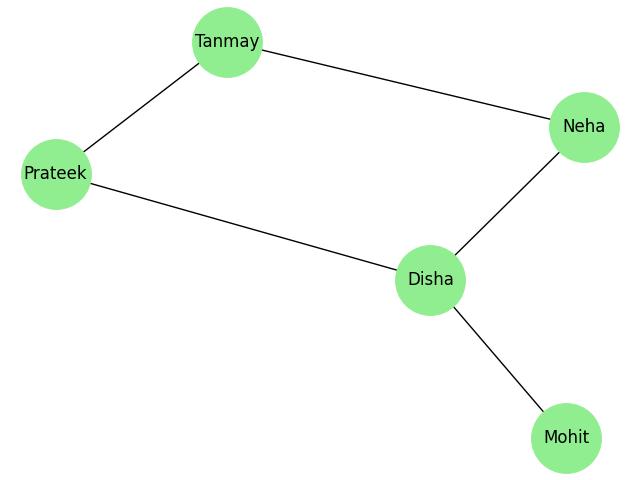
The above image visualizes a social network graph where each node represents a person, and edges represent their connections. The graph illustrates a web of relationships −
- Tanmay is directly connected to Neha and Prateek.
- While Neha and Prateek share a mutual connection with Disha.
- Disha is also connected to Mohit.
This forms a chain-like network with overlapping friendships. The graph shows both direct and indirect relationships within the network.
Example: Computer Network
In a computer network, computers are represented as nodes, and connections (e.g., Ethernet or wireless links) are represented as undirected edges. This graph represents the physical or logical topology of a network −
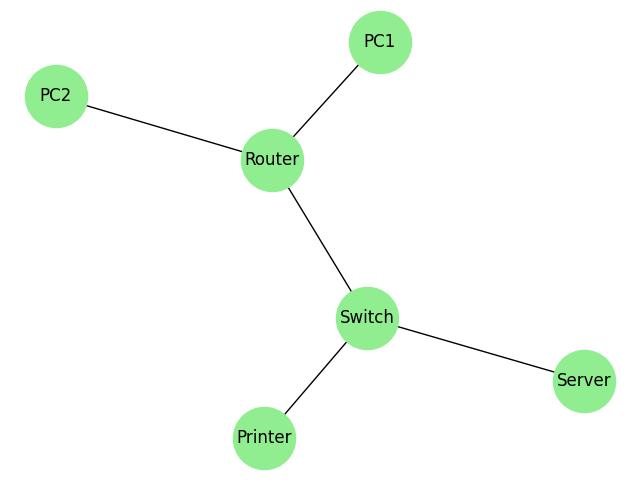
The above image visualizes a computer network graph where nodes represent devices (e.g., PCs, Router, Switch, Server, Printer), and edges represent connections between them. The graph demonstrates how devices are interconnected −
- PCs (PC1 and PC2) connect to the network through the Router, which links to the Switch.
- The Switch, in turn, connects to a Server and a Printer, representing a structured and centralized computer network.
This visualization highlights the hierarchical arrangement of network components.
Examples of Directed Graphs
A directed graph, or digraph, consists of vertices connected by edges with a specific direction. Directed graphs are useful in representing relationships where direction matters.
Example: Web Pages and Links
In the World Wide Web, web pages are represented as nodes, and hyperlinks between pages are represented as directed edges. This structure forms a directed graph.
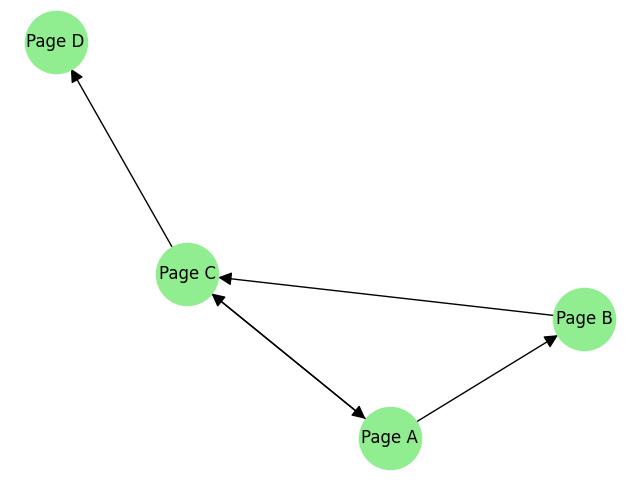
The above image visualizes a directed graph representing web pages and their hyperlinks. Each node corresponds to a web page, and directed edges indicate links between them. The graph shows that −
- "Page A" links to "Page B" and "Page C.
- While "Page B" also links to "Page C.
- "Page C" links back to "Page A" and also to "Page D".
This visualization shows the interconnectivity of web pages, including circular and one-way links, demonstrating how navigation flows through the network.
Example: Task Scheduling
In task scheduling, tasks are represented as nodes, and dependencies between tasks are represented as directed edges. A directed acyclic graph (DAG) is often used to represent task precedence.
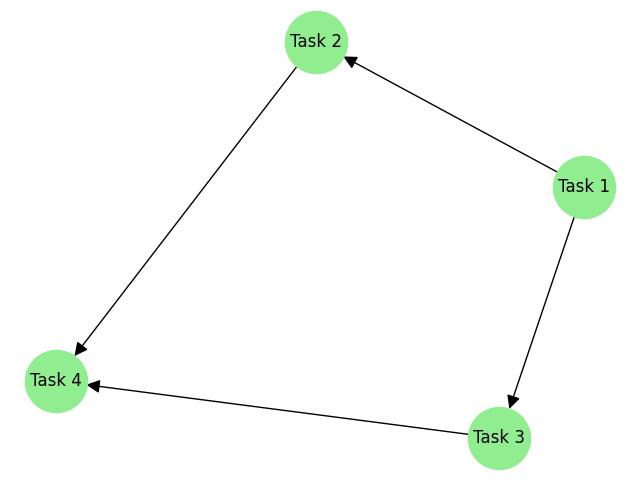
The above image visualizes a directed acyclic graph (DAG) representing a task scheduling sequence. Each node represents a task, and directed edges indicate dependencies between them. The graph shows that −
- "Task 1" must be completed before "Task 2" and "Task 3.
- While both "Task 2" and "Task 3" must be completed before "Task 4".
This visualization represents the flow of task execution, ensuring dependencies are met without creating any cycles, which is essential for scheduling and project management.
Examples of Weighted Graphs
Weighted graphs assign a weight or cost to each edge, representing distances, costs, or capacities. Weighted graphs are commonly used in optimization problems.
Example: Road Network
A road network can be represented as a weighted graph where intersections are nodes, roads are edges, and weights represent distances or travel times.
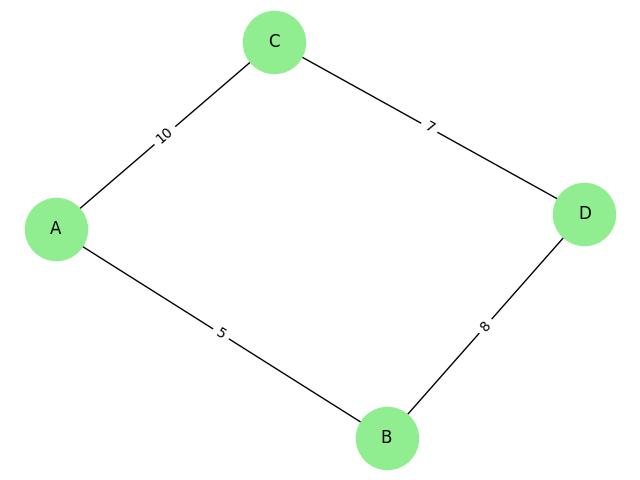
The above image visualizes a weighted graph representing a road network, where nodes represent locations, and edges represent roads connecting them. Each edge has an associated weight indicating the road's distance or cost.
For example, the weight of the edge between "A" and "B" is 5, while between "A" and "C" it is 10. The graph highlights the connectivity of locations along with their corresponding distances, which can be useful for route planning or analyzing transportation networks.
Spanning Trees
A spanning tree of a graph is a subgraph that is a tree, includes all vertices, and has the minimum number of edges possible to maintain connectivity. Let us determine the number of spanning trees for the given graph.
Example: Finding Number of Spanning Trees
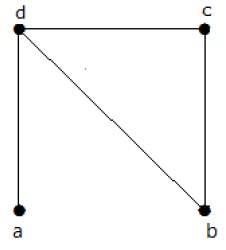
The graph has 3 spanning trees. Below are the spanning trees derived from the given graph −
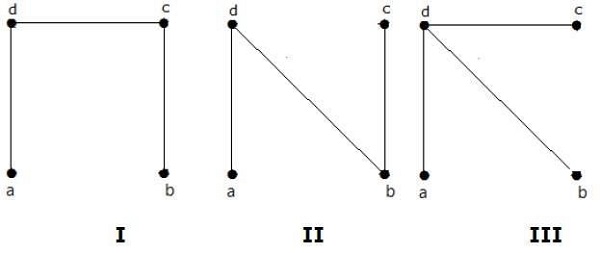
Here,
- Tree I: This spanning tree includes the edges AB, BC, and AD. It connects all the vertices while avoiding cycles.
- Tree II: Similar to Tree I, this spanning tree is formed using edges AC, CB, and AD.
- Tree III: This tree connects the vertices using edges AB, BD, and CD, forming another distinct spanning tree.
Among these spanning trees, Trees I and II are isomorphic, meaning they have the same structure. The only non-isomorphic trees are Trees I and III. Therefore, the total number of non-isomorphic spanning trees is 2.
Non-Isomorphic Graphs
Non-isomorphic graphs are graphs that cannot be transformed into one another simply by renaming vertices. Let us identify how many such graphs are possible with 3 vertices.
Example: How Many Non-Isomorphic Graphs Exist with 3 Vertices?
For 3 vertices, there are 4 non-isomorphic graphs. These graphs are depicted below −
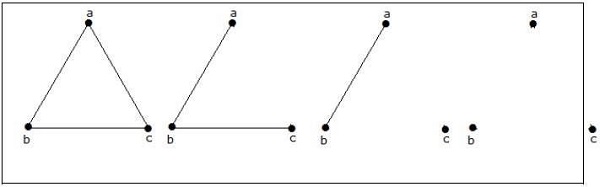
These are,
- Graph 1: A graph with 3 isolated vertices, meaning no edges connect them.
- Graph 2: A graph with one edge connecting two vertices, leaving the third vertex isolated.
- Graph 3: A graph with two edges forming a "V" shape, leaving no isolated vertices.
- Graph 4: A complete graph where every vertex is connected to every other vertex.
Planar Graph
A planar graph drawing makes sure that no edges cross each other. This method is used for graphs that can be drawn on a flat surface without any overlapping lines.
Example: Number of Regions in Planar Graph
Let us calculate the number of regions in a planar graph. The graph is connected, has 20 vertices, and each vertex has a degree of 3.
Solution
We start with the sum of degrees theorem −
deg(Vi) = 2|E| 20(3) = 2|E| |E| = 30
Now, applying Euler's formula for planar graphs −
|V| + |R| = |E| + 2 20 + |R| = 30 + 2 |R| = 12
Hence, the number of regions in the graph is 12.
Chromatic Number
The chromatic number of a graph is the minimum number of colors needed to color the graph such that no two adjacent vertices have the same color. Let us find the chromatic number for a complete graph, Kn.
Example: Chromatic Number of Complete Graph (Kn)
In a complete graph, each vertex is connected to every other vertex. To ensure no two adjacent vertices share the same color, each vertex must have its own unique color. Thus, the chromatic number of a complete graph, Kn, is −
Chromatic number (Kn) = n
For example, a K4 graph requires 4 colors, as there are 4 vertices, and all are connected to one another.
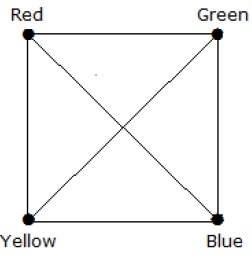
Matching Number
The matching number of a graph is the maximum number of edges that can be chosen such that no two edges share a vertex. Let us determine the matching number for the given graph.
Example: Matching Number of a Graph
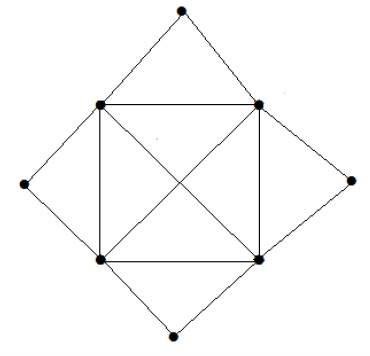
For the given graph −
- There are 9 vertices in total.
- A maximum of 4 edges can be selected, such that no two edges share a vertex.
Therefore, the matching number of the graph is 4.
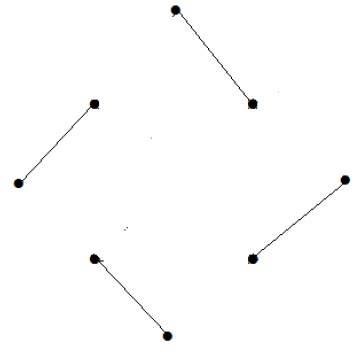
Covering Number
The line covering number of a graph is the minimum number of edges required to cover all the vertices in the graph. Let us calculate the line covering number for the given graph.
Example: Line Covering Number
For the given graph −
- There are 7 vertices in total (|V| = 7).
- Using the formula 1 [n/2], where n is the number of vertices:
1 [7/2] = 3
By using 3 edges, we can cover all the vertices in the graph. Thus, the line covering number is 3.
Real-World Applications of Graph Theory
Graph theory has various real-world applications across different fields. Below are some examples −
- Telecommunications: Representing communication networks, including telephone and internet connections.
- Transportation: Planning routes and optimizing traffic flow using road and railway networks.
- Biology: Analyzing protein-protein interaction networks and genetic pathways.
- Social Sciences: Studying social interactions, influence, and collaboration using social networks.