
- Graph Theory - Home
- Graph Theory - Introduction
- Graph Theory - History
- Graph Theory - Fundamentals
- Graph Theory - Applications
- Types of Graphs
- Graph Theory - Types of Graphs
- Graph Theory - Simple Graphs
- Graph Theory - Multi-graphs
- Graph Theory - Directed Graphs
- Graph Theory - Weighted Graphs
- Graph Theory - Bipartite Graphs
- Graph Theory - Complete Graphs
- Graph Theory - Subgraphs
- Graph Theory - Trees
- Graph Theory - Forests
- Graph Theory - Planar Graphs
- Graph Theory - Hypergraphs
- Graph Theory - Infinite Graphs
- Graph Theory - Random Graphs
- Graph Representation
- Graph Theory - Graph Representation
- Graph Theory - Adjacency Matrix
- Graph Theory - Adjacency List
- Graph Theory - Incidence Matrix
- Graph Theory - Edge List
- Graph Theory - Compact Representation
- Graph Theory - Incidence Structure
- Graph Theory - Matrix-Tree Theorem
- Graph Properties
- Graph Theory - Basic Properties
- Graph Theory - Coverings
- Graph Theory - Matchings
- Graph Theory - Independent Sets
- Graph Theory - Traversability
- Graph Theory Connectivity
- Graph Theory - Connectivity
- Graph Theory - Vertex Connectivity
- Graph Theory - Edge Connectivity
- Graph Theory - k-Connected Graphs
- Graph Theory - 2-Vertex-Connected Graphs
- Graph Theory - 2-Edge-Connected Graphs
- Graph Theory - Strongly Connected Graphs
- Graph Theory - Weakly Connected Graphs
- Graph Theory - Connectivity in Planar Graphs
- Graph Theory - Connectivity in Dynamic Graphs
- Special Graphs
- Graph Theory - Regular Graphs
- Graph Theory - Complete Bipartite Graphs
- Graph Theory - Chordal Graphs
- Graph Theory - Line Graphs
- Graph Theory - Complement Graphs
- Graph Theory - Graph Products
- Graph Theory - Petersen Graph
- Graph Theory - Cayley Graphs
- Graph Theory - De Bruijn Graphs
- Graph Algorithms
- Graph Theory - Graph Algorithms
- Graph Theory - Breadth-First Search
- Graph Theory - Depth-First Search (DFS)
- Graph Theory - Dijkstra's Algorithm
- Graph Theory - Bellman-Ford Algorithm
- Graph Theory - Floyd-Warshall Algorithm
- Graph Theory - Johnson's Algorithm
- Graph Theory - A* Search Algorithm
- Graph Theory - Kruskal's Algorithm
- Graph Theory - Prim's Algorithm
- Graph Theory - Borůvka's Algorithm
- Graph Theory - Ford-Fulkerson Algorithm
- Graph Theory - Edmonds-Karp Algorithm
- Graph Theory - Push-Relabel Algorithm
- Graph Theory - Dinic's Algorithm
- Graph Theory - Hopcroft-Karp Algorithm
- Graph Theory - Tarjan's Algorithm
- Graph Theory - Kosaraju's Algorithm
- Graph Theory - Karger's Algorithm
- Graph Coloring
- Graph Theory - Coloring
- Graph Theory - Edge Coloring
- Graph Theory - Total Coloring
- Graph Theory - Greedy Coloring
- Graph Theory - Four Color Theorem
- Graph Theory - Coloring Bipartite Graphs
- Graph Theory - List Coloring
- Advanced Topics of Graph Theory
- Graph Theory - Chromatic Number
- Graph Theory - Chromatic Polynomial
- Graph Theory - Graph Labeling
- Graph Theory - Planarity & Kuratowski's Theorem
- Graph Theory - Planarity Testing Algorithms
- Graph Theory - Graph Embedding
- Graph Theory - Graph Minors
- Graph Theory - Isomorphism
- Spectral Graph Theory
- Graph Theory - Graph Laplacians
- Graph Theory - Cheeger's Inequality
- Graph Theory - Graph Clustering
- Graph Theory - Graph Partitioning
- Graph Theory - Tree Decomposition
- Graph Theory - Treewidth
- Graph Theory - Branchwidth
- Graph Theory - Graph Drawings
- Graph Theory - Force-Directed Methods
- Graph Theory - Layered Graph Drawing
- Graph Theory - Orthogonal Graph Drawing
- Graph Theory - Examples
- Computational Complexity of Graph
- Graph Theory - Time Complexity
- Graph Theory - Space Complexity
- Graph Theory - NP-Complete Problems
- Graph Theory - Approximation Algorithms
- Graph Theory - Parallel & Distributed Algorithms
- Graph Theory - Algorithm Optimization
- Graphs in Computer Science
- Graph Theory - Data Structures for Graphs
- Graph Theory - Graph Implementations
- Graph Theory - Graph Databases
- Graph Theory - Query Languages
- Graph Algorithms in Machine Learning
- Graph Neural Networks
- Graph Theory - Link Prediction
- Graph-Based Clustering
- Graph Theory - PageRank Algorithm
- Graph Theory - HITS Algorithm
- Graph Theory - Social Network Analysis
- Graph Theory - Centrality Measures
- Graph Theory - Community Detection
- Graph Theory - Influence Maximization
- Graph Theory - Graph Compression
- Graph Theory Real-World Applications
- Graph Theory - Network Routing
- Graph Theory - Traffic Flow
- Graph Theory - Web Crawling Data Structures
- Graph Theory - Computer Vision
- Graph Theory - Recommendation Systems
- Graph Theory - Biological Networks
- Graph Theory - Social Networks
- Graph Theory - Smart Grids
- Graph Theory - Telecommunications
- Graph Theory - Knowledge Graphs
- Graph Theory - Game Theory
- Graph Theory - Urban Planning
- Graph Theory Useful Resources
- Graph Theory - Quick Guide
- Graph Theory - Useful Resources
- Graph Theory - Discussion
Graph Theory - 2-Vertex-Connected Graphs
2-Vertex-Connected Graphs
A 2-vertex-connected graph (or biconnected) is a graph that remains connected even after the removal of any one of its vertices. In other words, there is no single vertex whose removal would disconnect the graph.
A graph G = (V,E) is 2-vertex connected if, for any two vertices u and v in G, there is a path between "u" and "v" that does not pass through any vertex other than "u" and "v". This means that the graph cannot be disconnected by removing a single vertex.
Properties of 2-Vertex-Connected Graphs
The 2-vertex-connected graph have several properties, such as −
- Presence of a Path: Between any two vertices in a 2-vertex-connected graph, there are at least two disjoint paths that do not share any vertices other than the endpoints. These are known as vertex-disjoint paths.
- No Cut Vertices: A 2-vertex-connected graph has no articulation points. Removing any single vertex will not disconnect the graph.
- Subgraph Connectivity: Any subgraph of a 2-vertex-connected graph that includes the original vertices (except for the removed vertex) will also be connected.
- Strong Connectivity: A 2-vertex-connected graph remains connected even if any one of its vertices is removed.
A cut vertex (or articulation point) in a graph is a vertex whose removal increases the number of connected components of the graph. In a 2-vertex-connected graph, no such cut vertex exists, which makes it a more strong structure for networks and other applications.
Conditions for 2-Vertex-Connectivity
A graph is 2-vertex-connected if and only if it satisfies the following conditions −
- It is connected, meaning there is a path between any pair of vertices in the graph.
- There are no cut vertices in the graph. Removing any vertex will not disconnect the graph.
For example, consider the graph below −
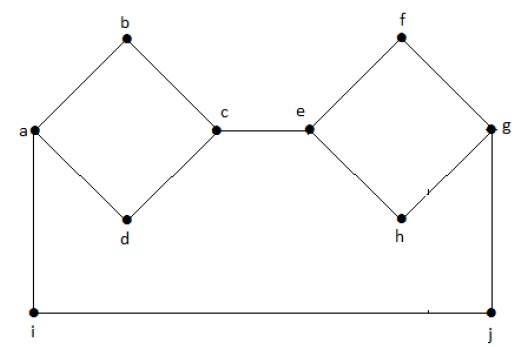
In this graph, removing any single vertex does not disconnect the graph. Therefore, the graph is 2-vertex-connected, as removing C and A vertices disconnects the graph.
Example: 2-Vertex-Connected Graph
The following graph is an example of a 2-vertex-connected graph −
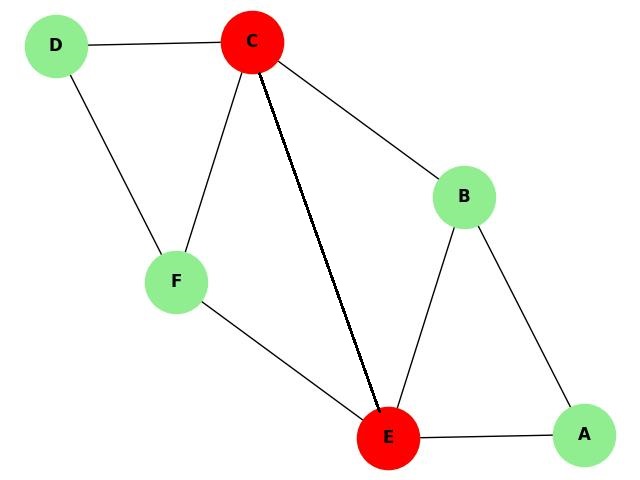
In the above given graph, removing any single vertex does not disconnect the graph, but removing two vertices (e.g., C and E) will disconnect the graph.
Applications of 2-Vertex-Connected Graphs
2-vertex-connected graphs have various real-world applications, especially in fields where reliability and fault tolerance are important:
- Communication Networks: In communication networks, biconnected graphs ensure that there are multiple paths for data transmission. Even if a node fails, the network remains operational.
- Strong Infrastructure Design: In infrastructure systems such as transportation networks, power grids, and pipelines, biconnectivity guarantees that the failure of a single component does not lead to system failure.
- Distributed Computing: In distributed computing systems, 2-vertex-connected graphs ensure that the network of computers can still function even if one of the computers fails.
- Network Reliability: Biconnectivity is an important concept in designing networks that are strong to node failures and can continue to operate without significant loss of service.
Testing 2-Vertex-Connectivity
There are various ways to test if a graph is 2-vertex-connected, such as −
- DFS-Based Algorithm: By performing a DFS traversal and checking for articulation points, we can determine if the graph is biconnected.
- Minimum Degree Condition: A graph with a minimum degree of at least 2 and a connected structure is 2-vertex-connected. However, this condition is not always sufficient, as some graphs may still have articulation points.
- Edge-Connectivity Method: The edge-connectivity of a graph is the minimum number of edges that must be removed to disconnect the graph. If the edge-connectivity is greater than 1, the graph is likely 2-vertex-connected.
2-Vertex-Connectivity in Various Graphs
Following are the lists of various types of graph and its 2-vertex-connectivity −
| Graph Type | 2-Vertex-Connected | Notes |
|---|---|---|
| Simple Path | No | Removing any vertex disconnects the path. |
| Cycle Graph | Yes | Any vertex removal still leaves a connected path. |
| Complete Graph (Kn) | Yes | For n 3, removing any vertex does not disconnect the graph. |
| Star Graph | No | Removing the central vertex disconnects the graph. |
| Wheel Graph | Yes | For n 4, removing any single vertex does not disconnect the graph. |
| Tree | No | Removing a non-leaf vertex disconnects the tree. |
| Grid Graph | Depends | Depends on the structure; inner vertices typically ensure connectivity. |
| Bipartite Graph | Depends | Depends on the structure; needs specific connectivity conditions. |
| Planar Graph | Depends | Depends on the structure; specific planar embeddings can ensure 2-vertex connectivity. |
| Hypercube | Yes | Removing any single vertex does not disconnect the graph. |