Graph Theory - Floyd-Warshall Algorithm

Previous
Quiz
Next

Floyd-Warshall Algorithm

The Floyd-Warshall algorithm is used to find the shortest paths between all pairs of vertices in a weighted graph.

It works for both directed and undirected graphs and can handle graphs with negative weights, but it does not work with graphs containing negative weight cycles.

Floyd-Warshall Algorithm Overview

The Floyd-Warshall algorithm calculates the shortest paths between all pairs of vertices in a graph by iteratively updating the shortest paths between every pair of nodes. It relies on dynamic programming and systematically explores each intermediate vertex to check if it provides a shorter path between two nodes.

The algorithm is based on the principle of relaxation, where it iteratively improves the shortest path estimates between nodes by considering intermediate vertices. Initially, it assumes that the shortest path between two vertices is the direct edge between them, and it updates this assumption by checking if a path through an intermediate vertex is shorter.

Steps of the Floyd-Warshall Algorithm

The algorithm proceeds in the following steps −

  • Initialize a distance matrix where dist[i][j] is the weight of the direct edge from vertex i to vertex j, or infinity if no edge exists.
  • Iterate through each vertex k as an intermediate vertex, and for each pair of vertices (i, j), check if the path from i to j through k is shorter than the direct path. If it is, update dist[i][j] with the shorter path length.
  • Repeat the process for all vertices k, i, and j to update the shortest path distances between every pair of vertices.
  • After the algorithm terminates, the distance matrix will contain the shortest path lengths between every pair of vertices.

Example of Floyd-Warshall Algorithm

Consider the following weighted graph −

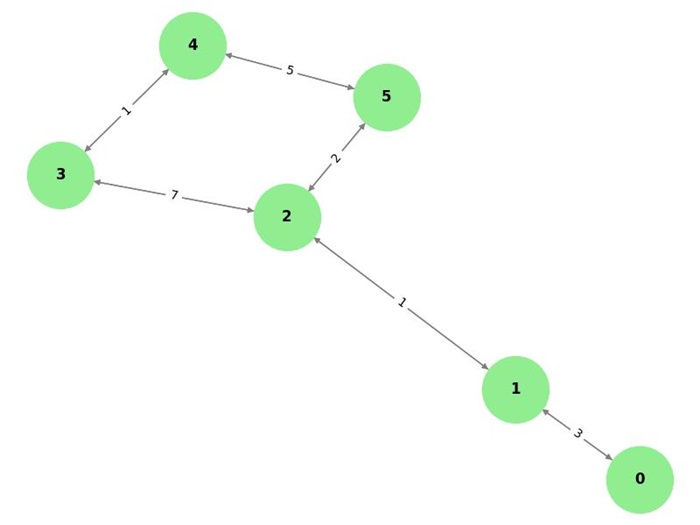
Floyd-Warshall Algorithm

The graph can be represented as the following adjacency matrix, where the value at dist[i][j] represents the weight of the edge from vertex i to vertex j −

dist = [
   [0, 3, inf, inf, inf, inf],
   [3, 0, 1, inf, inf, inf],
   [inf, 1, 0, 7, inf, 2],
   [inf, inf, 7, 0, 1, inf],
   [inf, inf, inf, 1, 0, 5],
   [inf, inf, 2, inf, 5, 0]
]

Here, dist[0][1] = 3 means there is an edge from vertex 0 to vertex 1 with weight 3, and dist[0][2] = inf means there is no direct edge between vertex 0 and vertex 2.

Step 1: Initialization

We initialize the distance matrix with the direct edges between vertices:

dist = [
   [0, 3, inf, inf, inf, inf],
   [3, 0, 1, inf, inf, inf],
   [inf, 1, 0, 7, inf, 2],
   [inf, inf, 7, 0, 1, inf],
   [inf, inf, inf, 1, 0, 5],
   [inf, inf, 2, inf, 5, 0]
]

Step 2: Iteration with k = 0

We now check if any shorter paths can be found through vertex 0. For each pair of vertices i and j, we check if dist[i][j] > dist[i][0] + dist[0][j]. If true, update dist[i][j] with the shorter path.

For example:

  • For dist[1][2], we check if dist[1][2] > dist[1][0] + dist[0][2], or 1 > 3 + inf. No update is made since dist[1][0] + dist[0][2] is infinity.
  • For dist[2][4], we check if dist[2][4] > dist[2][0] + dist[0][4], or inf > inf + inf. No update is made.

After this iteration, the matrix remains unchanged for k = 0:

dist = [
   [0, 3, inf, inf, inf, inf],
   [3, 0, 1, inf, inf, inf],
   [inf, 1, 0, 7, inf, 2],
   [inf, inf, 7, 0, 1, inf],
   [inf, inf, inf, 1, 0, 5],
   [inf, inf, 2, inf, 5, 0]
]

Step 3: Iteration with k = 1

Next, we check for shorter paths through vertex 1. For each pair (i, j), we check if dist[i][j] > dist[i][1] + dist[1][j]. If true, update dist[i][j] with the shorter path.

For example:

  • For dist[0][2], we check if dist[0][2] > dist[0][1] + dist[1][2], or inf > 3 + 1, which is true. Thus, we update dist[0][2] to 4.
  • For dist[3][5], we check if dist[3][5] > dist[3][1] + dist[1][5], or inf > inf + inf. No update is made.

After this iteration, the matrix is updated to:

dist = [
   [0, 3, 4, inf, inf, inf],
   [3, 0, 1, inf, inf, inf],
   [4, 1, 0, 7, inf, 2],
   [inf, inf, 7, 0, 1, inf],
   [inf, inf, inf, 1, 0, 5],
   [inf, inf, 2, inf, 5, 0]
]

Step 4: Further Iterations

The process continues for the remaining intermediate vertices k = 2, k = 3, and so on, progressively refining the distance matrix. After all iterations, the final distance matrix will contain the shortest paths between all pairs of vertices.

Step 1: Initialization
[0, 3, '', '', '', '']
[3, 0, 1, '', '', '']
['', 1, 0, 7, '', 2]
['', '', 7, 0, 1, '']
['', '', '', 1, 0, 5]
['', '', 2, '', 5, 0]

Step 2: Iteration with k = 0
[0, 3, '', '', '', '']
[3, 0, 1, '', '', '']
['', 1, 0, 7, '', 2]
['', '', 7, 0, 1, '']
['', '', '', 1, 0, 5]
['', '', 2, '', 5, 0]

Step 3: Iteration with k = 1
[0, 3, 4, '', '', '']
[3, 0, 1, '', '', '']
[4, 1, 0, 7, '', 2]
['', '', 7, 0, 1, '']
['', '', '', 1, 0, 5]
['', '', 2, '', 5, 0]

Step 3: Iteration with k = 2
[0, 3, 4, 11, '', 6]
[3, 0, 1, 8, '', 3]
[4, 1, 0, 7, '', 2]
[11, 8, 7, 0, 1, 9]
['', '', '', 1, 0, 5]
[6, 3, 2, 9, 5, 0]

Step 4: Iteration with k = 3
[0, 3, 4, 11, 12, 6]
[3, 0, 1, 8, 9, 3]
[4, 1, 0, 7, 8, 2]
[11, 8, 7, 0, 1, 9]
[12, 9, 8, 1, 0, 5]
[6, 3, 2, 9, 5, 0]

Step 5: Iteration with k = 4
[0, 3, 4, 11, 12, 6]
[3, 0, 1, 8, 9, 3]
[4, 1, 0, 7, 8, 2]
[11, 8, 7, 0, 1, 6]
[12, 9, 8, 1, 0, 5]
[6, 3, 2, 6, 5, 0]

Step 6: Iteration with k = 5
[0, 3, 4, 11, 11, 6]
[3, 0, 1, 8, 8, 3]
[4, 1, 0, 7, 7, 2]
[11, 8, 7, 0, 1, 6]
[11, 8, 7, 1, 0, 5]
[6, 3, 2, 6, 5, 0]

Final distance matrix after all iterations
[0, 3, 4, 11, 11, 6]
[3, 0, 1, 8, 8, 3]
[4, 1, 0, 7, 7, 2]
[11, 8, 7, 0, 1, 6]
[11, 8, 7, 1, 0, 5]
[6, 3, 2, 6, 5, 0]

Complexity of Floyd-Warshall Algorithm

The time complexity of the Floyd-Warshall algorithm is O(V3), where V is the number of vertices in the graph. This is because the algorithm uses three nested loops, each iterating over all vertices.

The space complexity is O(V2), as it requires storing the distance matrix with V x V entries to represent the shortest paths between all pairs of vertices.

Applications of Floyd-Warshall Algorithm

The Floyd-Warshall algorithm has various applications, such as −

  • All-Pairs Shortest Path: The Floyd-Warshall algorithm is used to find the shortest path between every pair of vertices in a graph.
  • Network Analysis: It is used in network analysis to compute the shortest paths between every pair of nodes in a network, helping in routing and optimization.
  • Transitive Closure: The algorithm can be used to calculate the transitive closure of a directed graph, helping to determine reachability between nodes.
  • Graph Connectivity: It is used to analyze graph connectivity by finding paths between all pairs of vertices.

Floyd-Warshall Algorithm in Python

Following is an implementation of the Floyd-Warshall algorithm in Python −

def floyd_warshall(graph):
   # Initialize the distance matrix
   dist = [[float('inf')] * len(graph) for _ in range(len(graph))]
   for i in range(len(graph)):
      dist[i][i] = 0
   for u in range(len(graph)):
      for v, weight in graph[u]:
         dist[u][v] = weight

   # Perform the Floyd-Warshall algorithm
   for k in range(len(graph)):
      for i in range(len(graph)):
         for j in range(len(graph)):
            if dist[i][j] > dist[i][k] + dist[k][j]:
               dist[i][j] = dist[i][k] + dist[k][j]

   return dist

# Example graph (Adjacency list representation)
graph = [
   [(1, 3), (2, 4)],
   [(0, 3), (2, 1)],
   [(1, 1), (3, 7), (5, 2)],
   [(2, 7), (4, 1)],
   [(3, 1), (5, 5)],
   [(2, 2), (4, 5)]
]

# Executing Floyd-Warshall algorithm
distances = floyd_warshall(graph)
for row in distances:
   print(row)

This implementation computes the shortest paths between every pair of vertices in the graph using the Floyd-Warshall algorithm −

[0, 3, 4, 11, 11, 6]
[3, 0, 1, 8, 8, 3]
[4, 1, 0, 7, 7, 2]
[11, 8, 7, 0, 1, 6]
[11, 8, 7, 1, 0, 5]
[6, 3, 2, 6, 5, 0]
Print Page
Previous
Next
Advertisements