Graph Theory - Depth-First Search

Quiz

Depth-First Search (DFS)

Depth-First Search (DFS) is a graph traversal algorithm that explores as far as possible along each branch before backtracking. It starts at a selected node (often called the 'root') and explores each branch of the graph deeply before moving to another branch.

DFS is particularly useful in scenarios such as topological sorting, detecting cycles in a graph, finding connected components in an undirected graph, and solving problems related to maze exploration and pathfinding.

DFS can be implemented using recursion or using an explicit stack data structure. Unlike Breadth-First Search (BFS), which explores level by level, DFS dives deeper into the graph before backtracking.

DFS Algorithm

The DFS algorithm follows these basic steps −

Initialize a stack and mark the starting node as visited.
While the stack is not empty, pop a node from the stack.
Visit all unvisited neighboring nodes of the current node, mark them as visited, and push them onto the stack.
Repeat this process until all reachable nodes are visited.

Let us look at an example to understand how DFS works. Consider the following graph with nodes labeled A, B, C, D, and E −

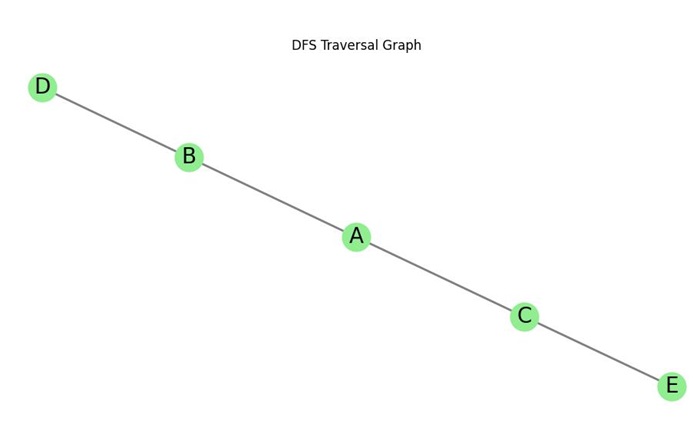
We will perform DFS starting from node A. The traversal proceeds as follows −

Start at node A. Mark it as visited and push it onto the stack.
Pop A from the stack, visit its neighbor B, mark it as visited, and push it onto the stack.
Pop B from the stack, visit its neighbor D, mark it as visited, and push it onto the stack.
Pop D from the stack. No unvisited neighbors.
Backtrack to B, then to A, and explore the next neighbor C.
Pop C from the stack, visit its neighbor E, mark it as visited, and push it onto the stack.
Pop E from the stack. No unvisited neighbors.

Thus, the DFS traversal order is A B D C E.

DFS on an Undirected Graph

In an undirected graph, DFS explores all reachable nodes starting from the chosen root node. It uses a stack to track nodes to visit next, ensuring that it explores deeply into each branch before backtracking.

Let us take an example of DFS traversal on an undirected graph −

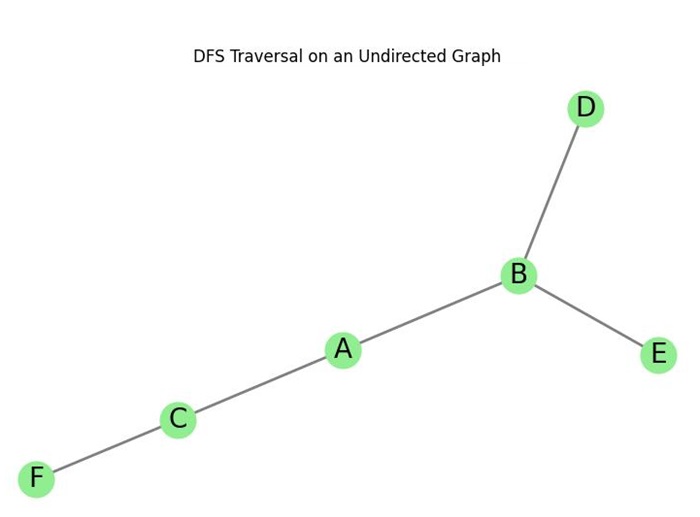
The graph is as follows −

A is connected to B and C.
B is connected to A, D, and E.
C is connected to A and F.
D is connected to B.
E is connected to B.
F is connected to C.

Starting DFS from node A:

Visit A, then push its neighbor B onto the stack.
Pop B, then push its neighbors D and E onto the stack.
Pop D. No unvisited neighbors.
Pop E. No unvisited neighbors.
Backtrack to A and push C onto the stack.
Pop C, then push its neighbor F onto the stack.
Pop F. No unvisited neighbors.

Final DFS traversal order: A B D E C F.

DFS on a Directed Graph

In directed graphs, DFS works similarly to undirected graphs, but it respects the direction of edges. DFS explores only the neighbors that are directly reachable from a node, following the directions of the edges.

Consider the following directed graph −

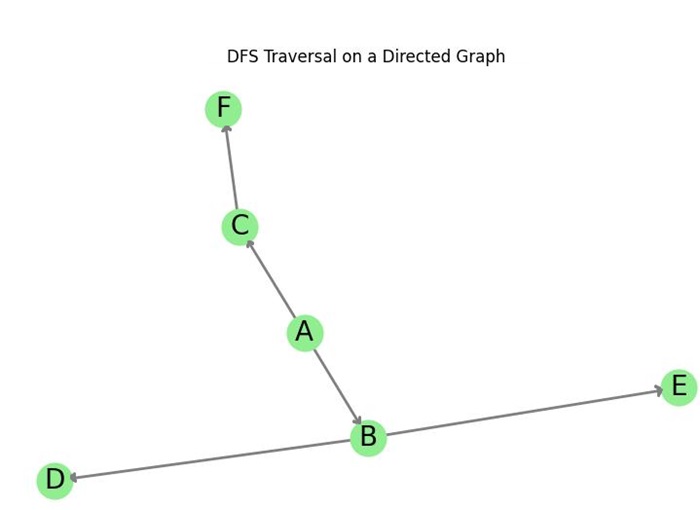
In this graph, we perform DFS starting from node A −

Start at node A, visit its neighbor B, and push it onto the stack.
Pop B, then visit its neighbor D and push it onto the stack.
Pop D. No unvisited neighbors.
Backtrack to B and visit its neighbor E, then push E onto the stack.
Pop E. No unvisited neighbors.
Backtrack to A and visit its neighbor C, then push C onto the stack.
Pop C, then visit its neighbor F and push it onto the stack.
Pop F. No unvisited neighbors.

Final DFS traversal order: A B D E C F.

Applications of DFS

DFS is used in various real-world applications, such as −

Topological Sorting: DFS is used to perform topological sorting of a Directed Acyclic Graph (DAG). This is useful for scheduling tasks, compiling programs, and managing dependencies.
Cycle Detection: DFS can help detect cycles in a graph. If, during DFS, we encounter a node that has already been visited and is still on the stack, it indicates the presence of a cycle.
Connected Components: DFS can be used to find connected components in an undirected graph by performing DFS starting from an unvisited node and marking all reachable nodes.
Pathfinding and Maze Exploration: DFS is used in solving maze puzzles, where it explores all possible paths deeply and backtracks when it reaches dead ends.
Solving Puzzles: DFS can be used to solve puzzles like Sudoku, N-Queens, and others by exploring all possible configurations and backtracking when necessary.

DFS for Pathfinding

DFS can be used for pathfinding in graphs, especially when finding one possible path is sufficient (not necessarily the shortest path). Since DFS dives deep into the graph, it will explore one potential path completely before backtracking to try another path.

For example, in a maze-solving scenario, DFS will explore one possible route from start to finish, backtrack when a dead-end is encountered, and continue searching for other paths until the exit is found.

Complexity of DFS

The time complexity of DFS is O(V + E), where V is the number of vertices and E is the number of edges in the graph. This is because DFS processes each vertex and edge exactly once.

The space complexity is O(V), as DFS requires storage for the stack and a visited list, both of which require space proportional to the number of vertices in the graph.

DFS performs efficiently on both sparse and dense graphs, making it suitable for various graph-related problems.

DFS with Backtracking

DFS with backtracking is a variation of DFS where, after exploring a node, the algorithm backtracks and tries to explore alternative paths. This is especially useful in solving constraint satisfaction problems such as N-Queens, Sudoku, and puzzle solving.

In these cases, DFS explores different configurations of the problem, and backtracking is used when an invalid configuration is reached (such as placing two queens in the same row in the N-Queens problem).

DFS Implementation (Python)

Here is an example of how you can implement DFS using recursion in Python. The algorithm uses a stack (implicitly through recursion) to manage the nodes to be explored and a set to keep track of visited nodes −

def dfs(graph, node, visited=None):
   if visited is None:
   # Set to track visited nodes
      visited = set()  
    
   # Mark the current node as visited
   visited.add(node)  
   # Print the current node
   print(node, end=" ")  
    
   # Recursively visit all unvisited neighbors
   for neighbor in graph[node]:
      if neighbor not in visited:
         dfs(graph, neighbor, visited)

# graph (Adjacency List)
graph = {
   'A': ['B', 'C'],
   'B': ['A', 'D', 'E'],
   'C': ['A', 'F'],
   'D': ['B'],
   'E': ['B'],
   'F': ['C']
}

# Perform DFS starting from node 'A'
dfs(graph, 'A')

This code illustrates how DFS explores the graph deeply by visiting nodes along a branch before backtracking −

A B D E C F

Print Page