Graph Algorithms in Machine Learning

---

---

Graph Algorithms in Machine Learning

Graph algorithms are useful in machine learning for understanding complex relationships in data. They help analyze connected structures like social networks, recommendation systems, biological networks, and knowledge graphs.

These algorithms are used for tasks like clustering, classification, anomaly detection, and prediction.

Machine learning applications often require understanding patterns, relationships, and structures in data. Graph algorithms provide ways to extract meaningful insights from structured and unstructured data.

This tutorial explores the fundamentals of graph algorithms used in machine learning, their applications, and how they contribute to various tasks in AI and data science.

Why Use Graph Algorithms in ML?

Graphs naturally represent relationships between entities, making them useful in various fields −

• Social Networks: Analyzing user interactions and detecting communities.
• Recommendation Systems: Suggesting products or content based on user preferences.
• Biological Networks: Studying protein-protein interactions and gene regulatory networks.
• Fraud Detection: Identifying suspicious activities by analyzing transaction networks.
• Natural Language Processing: Representing text as a graph for better contextual understanding.

Graph Algorithms in Machine Learning

There are various graph algorithms commonly used in machine learning tasks. These are as follows −

• Graph Traversal: Used for pathfinding and exploring connected components.
• Shortest Path Algorithms: Finding optimal routes in graph-based networks.
• Centrality Measures: Identifying influential nodes in a network.
• Graph Clustering: Grouping similar nodes based on connectivity.
• Graph Neural Networks (GNNs): Deep learning models designed for graph data.

Graph Traversal Algorithms

Graph traversal is the process of visiting all nodes in a graph systematically. The two most common traversal methods are:

Breadth-First Search (BFS)

BFS explores all neighbors of a node before moving to the next level. It is useful for:

• Finding the shortest path in unweighted graphs.
• Detecting connected components.
• Recommendation systems.

Example: Implementing BFS in Python

The following BFS (Breadth-First Search) algorithm explores a graph level by level using a queue. It starts from node 'A', visits its neighbors before moving to the next level, printing each visited node −

from collections import deque

def bfs(graph, start):
   visited = set()
   queue = deque([start])
    
   while queue:
      node = queue.popleft()
      if node not in visited:
         print(node, end=" ")
         visited.add(node)
         queue.extend(graph[node])

graph = {
   'A': ['B', 'C'],
   'B': ['D', 'E'],
   'C': ['F'],
   'D': [], 'E': [], 'F': []
}

bfs(graph, 'A')

We get the output as shown below −

A B C D E F 

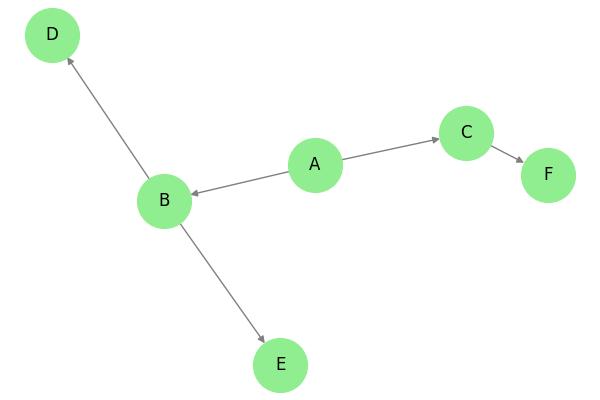
Depth-First Search (DFS)

DFS explores as deep as possible before backtracking. It is useful for −

• Finding cycles in a graph.
• Solving maze and pathfinding problems.
• Detecting strongly connected components.

Example: Implementing DFS in Python

This DFS (Depth-First Search) algorithm explores the same above graph by visiting a node and recursively traversing its neighbors before backtracking. It starts from 'A', exploring deeper paths before moving to the next branch −

from collections import deque

def dfs(graph, node, visited=set()):
   if node not in visited:
      print(node, end=" ")
      visited.add(node)
      for neighbor in graph[node]:
         dfs(graph, neighbor, visited)
graph = {
   'A': ['B', 'C'],
   'B': ['D', 'E'],
   'C': ['F'],
   'D': [], 'E': [], 'F': []
}

dfs(graph, 'A')

Following is the output obtained −

A B D E C F 

Shortest Path Algorithms

Shortest path algorithms are useful for finding the most efficient route between nodes in a graph. These algorithms are commonly used in real-world applications such as navigation systems, network routing, logistics, and recommendation engines. They help optimize resource usage, reduce travel time, and enhance decision-making in various domains.

Dijkstra's Algorithm

Dijkstra's Algorithm is used to find the shortest path from a single source node to all other nodes in a graph. It works well with weighted graphs where all edge weights are non-negative. It works in the following way −

• Initialize: Set the distance of the source node to 0 and all other nodes to infinity.
• Priority Queue: Use a min-priority queue (or min-heap) to select the node with the smallest distance.
• Relaxation Step: For the selected node, update the distances of its adjacent nodes if a shorter path is found.
• Mark as Processed: Once a node's shortest distance is determined, it is removed from the queue and not revisited.
• Repeat: Continue this process until all nodes have been visited.

Example

In the following example, we use Dijkstra's algorithm to find the shortest path from node A to all other nodes in a weighted graph −

• The graph is represented as an adjacency list where each node maps to a list of (neighbor, weight) pairs.
• A priority queue (min-heap) is used to select the node with the smallest distance at each step.
• The algorithm relaxes edges by updating the shortest distances when a better path is found.
• Once all nodes are processed, the dictionary shortest_paths contains the shortest distance from 'A' to every other node.

import heapq

def dijkstra(graph, start):
   pq = [(0, start)]
   distances = {node: float('inf') for node in graph}
   distances[start] = 0

   while pq:
      current_distance, node = heapq.heappop(pq)

      for neighbor, weight in graph[node].items():
         distance = current_distance + weight
         if distance < distances[neighbor]:
            distances[neighbor] = distance
            heapq.heappush(pq, (distance, neighbor))
    
   return distances

graph = {
   'A': {'B': 1, 'C': 4},
   'B': {'C': 2, 'D': 5},
   'C': {'D': 1},
   'D': {}
}

print(dijkstra(graph, 'A'))

Following is the output obtained −

{'A': 0, 'B': 1, 'C': 3, 'D': 4}

Graph Neural Networks (GNNs)

Graph Neural Networks (GNNs) are a type of deep learning model specifically designed to process and analyze graph-structured data. Unlike traditional neural networks, GNNs can capture relationships and dependencies between nodes in a graph.

They are widely used in applications such as social network analysis, recommendation systems, and drug discovery. They are also used in −

• Node classification.
• Link prediction.
• Graph classification.

Applications of Graph Algorithms in ML

Graph algorithms have many machine learning applications, such as −

• Social Media Analysis: Detecting communities and recommending connections.
• Fraud Detection: Identifying fraudulent transactions using graph anomalies.
• Biological Research: Analyzing molecular structures and gene interactions.
• Search Engines: Ranking web pages based on link structures.