Graph Theory - Cayley Graphs

---

---

Cayley Graphs

A Cayley graph is a special type of graph that represents the structure of a group, a fundamental concept in abstract algebra. It is constructed using a set of generators, which are a subset of the group elements, to define the group's structure.

This graph provides a visual representation of how the group elements relate to one another, capturing the group's symmetry and algebraic properties.

Formally, given a group G and a generating set S, the Cayley graph (G, S) is a directed graph where −

• Vertices: Each vertex corresponds to an element of the group G.
• Edges: There is a directed edge from vertex g to vertex h if and only if there is a generator s in S such that h = gs.

If the generating set S is symmetric (i.e., if s is in S, then s^-1 is also in S), the Cayley graph can be considered undirected by ignoring the direction of the edges.

Properties of Cayley Graphs

Cayley graphs have several important properties that reflect the structure of the underlying group. Following are some of the important properties −

• Vertex-transitivity: Cayley graphs are vertex-transitive, meaning that for any two vertices u and v, there exists an automorphism of the graph mapping u to v.
• Regularity: The degree of each vertex in a Cayley graph is equal to the size of the generating set S.
• Connectedness: The Cayley graph is connected if and only if the generating set S generates the group G.
• Symmetry: Cayley graphs exhibit a high degree of symmetry, which makes them useful for studying the algebraic structure of groups.

An automorphism is a transformation of a structure that maps the structure onto itself without changing its properties. In graph theory, it means a way to rearrange a graph's nodes while preserving the connections between them.

Graph Structure

The structure of a Cayley graph can vary significantly depending on the group and generating set. Here is an example of a Cayley graph for the group Z₄ (the integers modulo 4) with the generating set S = {1, 3}:

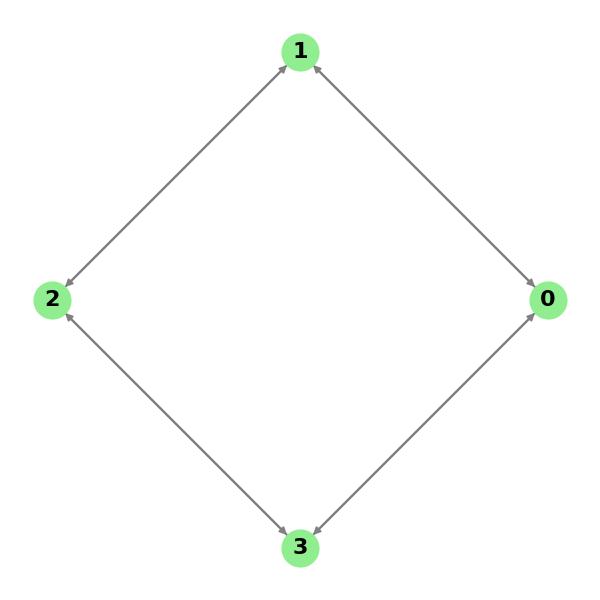
In this representation, the vertices correspond to the elements {0, 1, 2, 3} of Z₄, and edges are drawn according to the generating set {1, 3}.

Adjacency Matrix

The adjacency matrix of a Cayley graph provides a numerical representation of the graph's structure. For a Cayley graph (G, S), the adjacency matrix A is defined as follows −

A[i][j] = 1 if there exists a generator s in S such that g_i * s = g_j
          0 otherwise

Here is the adjacency matrix for the Cayley graph of Z₄ with generating set {1, 3} −

0 1 0 1
1 0 1 0
0 1 0 1
1 0 1 0

Construction of Cayley Graphs

Cayley graphs can be constructed using various methods. The most common approach involves defining a group and a generating set, and then drawing the corresponding graph. Here, we will describe two common methods: using permutations and using cosets.

Using Permutations

One way to construct a Cayley graph is by using permutations. This method involves defining the group as a set of permutations and the generating set as a subset of these permutations. The steps are as follows −

• Define the group G as a set of permutations on a finite set.
• Choose a generating set S from the permutations in G.
• Construct the graph by drawing vertices for each element of G and edges according to the generating set S.

For example, consider the symmetric group S₃ (the group of all permutations of 3 elements) with generating set {(12), (123)}. The resulting Cayley graph is −

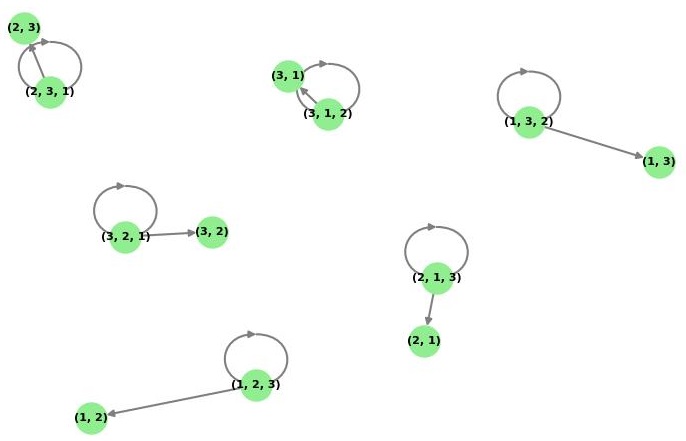
Using Cosets

Another method for constructing Cayley graphs is using cosets. This approach is particularly useful for studying quotient groups. The steps are as follows −

• Define the group G and a normal subgroup N.
• Choose a generating set S from the elements of G.
• Construct the quotient group G/N and the corresponding Cayley graph by drawing vertices for each coset and edges according to the generating set S.

For example, consider the group Z₆ with normal subgroup {0, 3} and generating set {1, 2}. The resulting Cayley graph is −

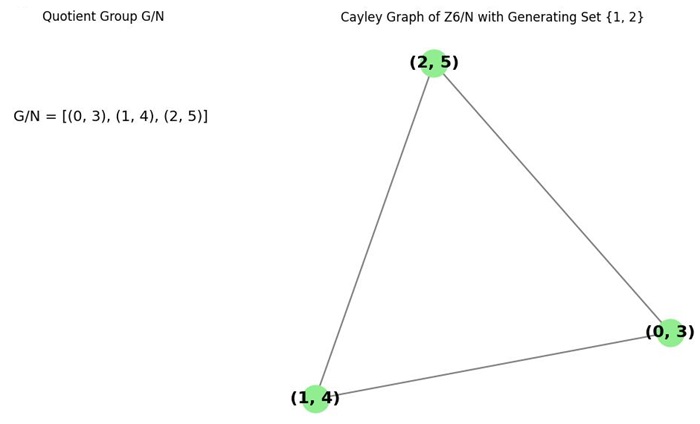
Applications of Cayley Graphs

Cayley graphs have various applications in mathematics, computer science, and other fields. Some of the applications are −

• Group Theory: Cayley graphs are used to visualize and study the structure of groups, including their subgroups, quotient groups, and automorphisms.
• Network Design: The symmetry and regularity of Cayley graphs make them useful in the design of efficient and fault-tolerant network topologies.
• Algorithm Design: Cayley graphs are used in the design and analysis of algorithms, particularly in the context of group-based computations and cryptography.
• Mathematical Puzzles: Cayley graphs appear in various mathematical puzzles and recreational mathematics problems due to their intriguing properties.