Graph Theory - Layered Graph Drawing

---

---

Layered Graph Drawing

Layered Graph Drawing is used to display graphs, especially directed acyclic graphs (DAGs), by arranging the nodes into horizontal layers. This method helps show the structure and relationships between nodes more clearly.

The primary goal is to organize the nodes into different levels or layers, and then draw the edges (connections) in a way that shows how the nodes are connected or how one depends on another. This layout makes it easier to understand the flow or direction of the graph.

A DAG (Directed Acyclic Graph) is a type of graph where the edges have a direction, meaning they go from one node to another, and there are no cycles. In other words, you cannot start at one node, follow the edges, and return to the same node.

The image below demonstrates a layered graph where nodes are placed in different layers to represent hierarchical relationships between them.

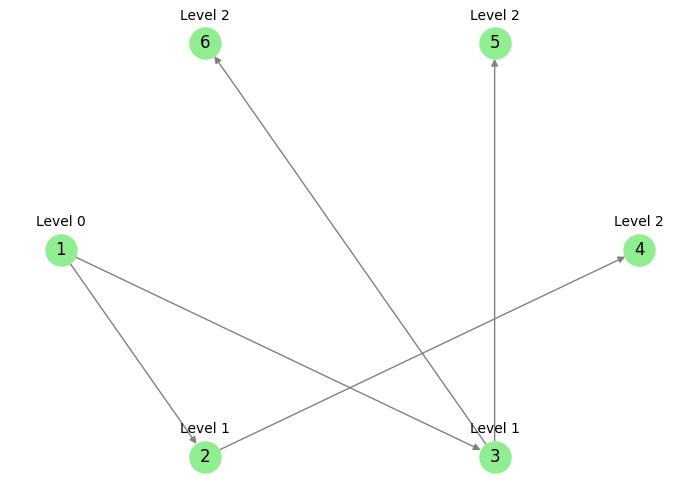
In this image, the levels of the nodes are assigned based on their distance (in terms of hops) from the root node (node 1). The "level" represents how deep a node is in the graph hierarchy, with the root node being at level 0 −

• The root node (1) is at level 0 because it is the starting point.
• Any node directly connected to the root node will be at level 1 (1 hop away from the root).
• Any node that is two edges away from the root will be at level 2, and so on.

Principles of Layered Graph Drawing

Layered graph drawing is based on several important principles that helps visualize hierarchical structures more clearly −

• Layer Assignment: Nodes are grouped into horizontal layers based on how they depend on each other, with each layer representing a step in the flow of information.
• Edge Routing: Connections (edges) between nodes are drawn between the layers. The goal is to reduce edge crossings to keep the graph easy to read.
• Ordering within Layers: Once the nodes are assigned to layers, their order within each layer is adjusted to further minimize the number of edge crossings.

Layered Graph Drawing Algorithms

There are different algorithms used to create layered graphs. These algorithms focus on organizing nodes into layers, ordering them within those layers, and minimizing edge crossings to make the graph clearer. Some common algorithms are −

• Sugiyama's Algorithm: A well-known algorithm that reduces edge crossings by carefully adjusting the order of nodes within layers.
• Bottom-Up Algorithm: This algorithm builds the layers starting from the leaves (nodes with no outgoing edges) and iteratively moves upwards to assign nodes to layers.
• Top-Down Algorithm: This algorithm assigns layers starting from the root node (generally the starting point of the graph) and works its way downward.
• Kang's Algorithm: A refined version of the bottom-up approach, focusing on reducing the number of edge crossings by adjusting node positions.

Sugiyama's Algorithm

Sugiyama's Algorithm is one of the most well-known approaches for layered graph drawing. It works in several phases:

• Phase 1 - Layer Assignment: The first step is to assign nodes to layers, where nodes that have no predecessors are placed at the bottom layer, and nodes with dependencies are placed higher.
• Phase 2 - Node Ordering: Once the layers are assigned, the nodes within each layer are ordered to minimize edge crossings.
• Phase 3 - Edge Routing: The edges are routed between the layers, ensuring that they do not cross each other unnecessarily.

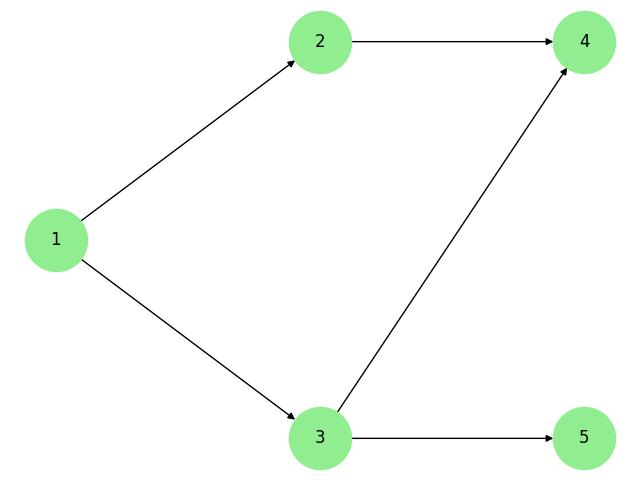
The above image demonstrates the result of applying Sugiyama's Algorithm to a layered graph, showing the nodes placed in horizontal layers with optimized edge routing.

Layered Graph Drawing with Python

Let us explore how to create a layered graph using Python's networkx library. Although networkx doesn't provide a direct implementation of Sugiyama's Algorithm, we can approximate layered graph drawing using a custom approach and basic graph layout algorithms.

In the following example, we are using the networkx library to create a simple directed graph and visualize it with layered drawing −

import networkx as nx
import matplotlib.pyplot as plt

# Create a directed graph
G = nx.DiGraph()
G.add_edges_from([(1, 2), (1, 3), (2, 4), (3, 4), (3, 5)])

# Define the position of nodes in layers
pos = {1: (0, 0), 2: (1, 1), 3: (1, -1), 4: (2, 1), 5: (2, -1)}

# Draw the graph with layers
nx.draw(G, pos, with_labels=True, node_color="lightgreen", edge_color="blue", node_size=2000)

# Display the graph
plt.title("Layered Graph Drawing")
plt.show()

The above code creates a simple directed graph and manually defines positions for each node to simulate a layered drawing. The nodes are placed at different levels to reflect their dependencies −

Challenges in Layered Graph Drawing

Although layered graph drawing is a helpful technique, it does come with its challenges as well −

• Edge Crossings: Even though efforts are made to reduce edge crossings, complex graphs may still have overlapping edges, making them hard to understand.
• Layer Assignment Complexity: Figuring out the best way to assign nodes to layers can be a difficult and time-consuming task, especially for larger graphs.
• Node Overlap: When there are too many nodes in the same layer, they may overlap, which reduces the graph's clarity.
• Graph Size: Large graphs with lots of nodes and edges can look messy and cluttered, even with well-designed algorithms to organize them.

Optimizations for Layered Graph Drawing

There are several ways to improve layered graph drawing and make the graphs easier to read and understand −

• Crossing Reduction: Algorithms like Sugiyama's Algorithm help reduce edge crossings by ordering the nodes in layers in the best way possible.
• Node Spacing: Adjusting the spacing between nodes in each layer can help avoid node overlap and make the graph clearer to read.
• Graph Simplification: For large graphs, simplifying the graph (e.g., by removing less important edges) can reduce complexity and make the layout more pleasant.
• Multi-Layer Graphs: Sometimes, grouping related nodes into single larger nodes or using multi-layered graphs can make the visualization easier to understand.