Graph Theory - De Bruijn Graphs

De Bruijn Graphs

In graph theory, a De Bruijn graph is a directed graph that represents the relationships between substrings of a fixed length in a sequence of symbols. The graph is named after the Dutch mathematician Neels De Bruijn, who introduced it in the 1940s.

A De Bruijn graph is a directed graph where −

• The vertices represent all possible substrings of a fixed length k from a given alphabet.
• The edges represent transitions between these substrings, where each edge corresponds to appending a symbol from the alphabet to a substring.

Formally, for a given alphabet Σ and length k, the De Bruijn graph B(k, |Σ|) has −

• Vertices: Each vertex represents a distinct string of length k-1 over the alphabet Σ.
• Edges: There is a directed edge from vertex v = v₁v₂...v_k-1 to vertex w = v₂v₃...v_k-1a if a is a symbol from the alphabet Σ.

De Bruijn Graph Construction

To construct a De Bruijn graph, follow these steps −

• Define the alphabet Σ and the length k of the substrings.
• Identify all possible strings of length k-1 over the alphabet Σ as the vertices.
• For each vertex v = v₁v₂...v_k-1, add a directed edge to the vertex v' = v₂v₃...v_k-1a for each symbol a in the alphabet Σ.

For example, consider the alphabet Σ = {0, 1} and k = 3. The possible vertices of the graph are all strings of length k-1 = 2, i.e., 00, 01, 10, 11.

The corresponding De Bruijn graph B(3, 2) will have the following edges −

• 00 00 (append 0), 00 01 (append 1)
• 01 10 (append 0), 01 11 (append 1)
• 10 00 (append 0), 10 01 (append 1)
• 11 10 (append 0), 11 11 (append 1)

This process can be generalized to construct De Bruijn graphs for different alphabets and substring lengths.

Applications of De Bruijn Graphs

De Bruijn graphs are widely used in various fields, particularly in the following areas −

• Bioinformatics: In DNA sequencing, De Bruijn graphs are used to assemble genomes from short DNA fragments.
• String matching: They are used for substring search, allowing fast identification of patterns within strings.
• Data compression: De Bruijn graphs are also used in algorithms for data compression, where they help in finding repeating patterns.
• Network routing: In some network applications, De Bruijn graphs help in optimizing routing by modeling the interconnections of nodes and transitions.

Properties of De Bruijn Graphs

De Bruijn graphs have several important properties, such as −

• Symmetry: De Bruijn graphs provide a high level of symmetry due to the regularity of the vertex and edge structure.
• Degree: Every vertex in a De Bruijn graph has an in-degree and out-degree equal to the size of the alphabet, |Σ|.
• Eulerian: De Bruijn graphs are Eulerian, meaning there exists an Eulerian circuit (a closed walk that visits every edge exactly once).

Visualizing De Bruijn Graphs

Following is an example of a De Bruijn graph for the alphabet Σ = {0, 1} and length k = 3.

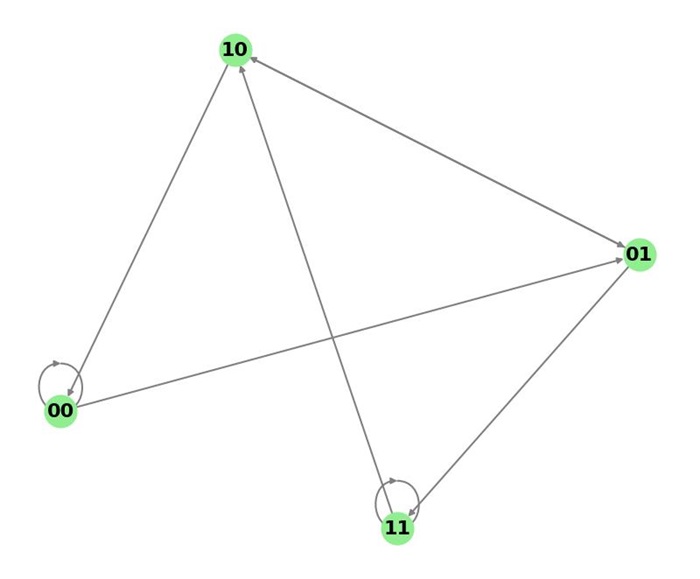
The above graph displays a De Bruijn graph for the binary alphabet {0, 1} and substrings of length 3, where the nodes represent the substrings, and the edges represent the transitions.

De Bruijn Graphs in DNA Sequencing

One of the most significant applications of De Bruijn graphs is in DNA sequencing, where they are used to assemble short DNA fragments into longer sequences. In this context −

• Each DNA fragment is represented as a vertex in the graph.
• Edges represent possible overlaps between these fragments.
• The goal is to find an Eulerian cycle in the graph that represents the original sequence of DNA.

The advantage of using De Bruijn graphs in DNA sequencing is that they provide a compact representation of the genome, reducing the complexity of the problem of assembling long DNA sequences from shorter fragments.