Graph Theory - Planarity and Kuratowski's Theorem

Quiz

Planarity in Graph Theory

Planarity in graph theory determines whether a graph can be drawn on a plane without any edges crossing each other, except at their endpoints. A graph that can be represented in this way is called a planar graph.

Planar graphs are important in many real-world applications, such as circuit design, network visualization, and geographical mapping, where minimizing edge intersections is important for clarity.

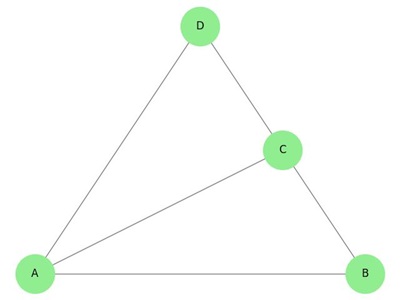
Properties of Planar Graphs

Planar graphs have specific characteristics that distinguish them from other types of graphs. These properties are used to determine the planarity of a graph −

Face Definition: A planar graph divides the plane into regions called faces. One of these faces is the outer, unbounded region.
Euler's Formula: For any connected planar graph, Euler's formula states that:
```
V - E + F = 2
```
Here, V is the number of vertices, E is the number of edges, and F is the number of faces.
Maximum Edges: A planar graph with n vertices can have at most 3n - 6 edges, provided n 3.

What is Kuratowski's Theorem?

Kuratowski's Theorem provides a condition to determine whether a graph is planar. According to the theorem −

A graph is planar if and only if it does not contain a subgraph that is a subdivision of K₅ (complete graph on 5 vertices) or K_3,3 (complete bipartite graph on 6 vertices, split into two sets of 3).

This theorem helps to identify non-planar graphs by checking for these forbidden subgraphs, even when the original graph appears more complex or has additional edges and vertices.

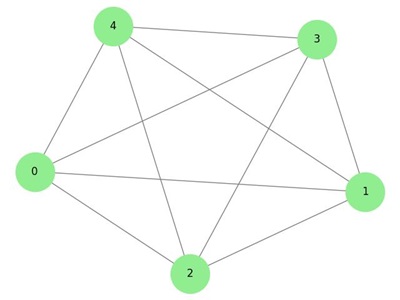
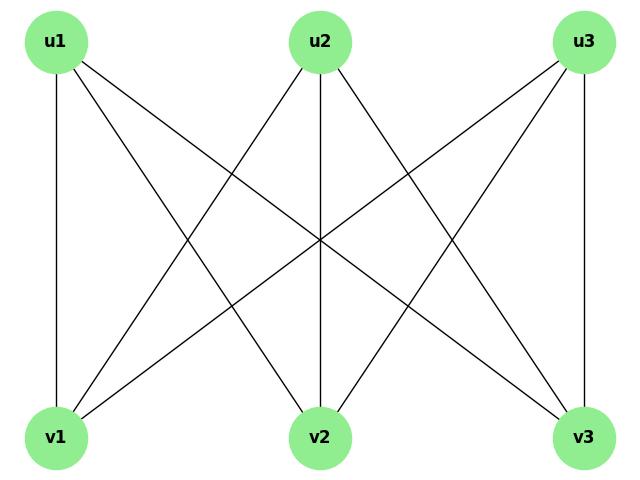
Understanding K₅ and K_3,3

To be fully familiar with Kuratowski's Theorem, it is important to understand the graphs K₅ and K_3,3 −

K₅: It is a complete graph with 5 vertices, where every vertex is connected to every other vertex. It is non-planar because it cannot be drawn without edge crossings.

K_3,3: A complete bipartite graph with two sets of 3 vertices, where every vertex in one set is connected to all vertices in the other set. It is also non-planar due to edge crossings.

Testing Graph Planarity

Graph planarity can be tested using various techniques, including the application of Kuratowski's Theorem. Following are the steps used −

Check if the graph has fewer than or equal to 3n - 6 edges. If not, the graph is non-planar.
Identify subgraphs within the graph. If any subgraph is a subdivision of K₅ or K_3,3, the graph is non-planar.
Use Euler's formula to verify the relationship between vertices, edges, and faces.

Examples of Planar and Non-Planar Graphs

Following are few examples illustrating planar and non-planar graphs −

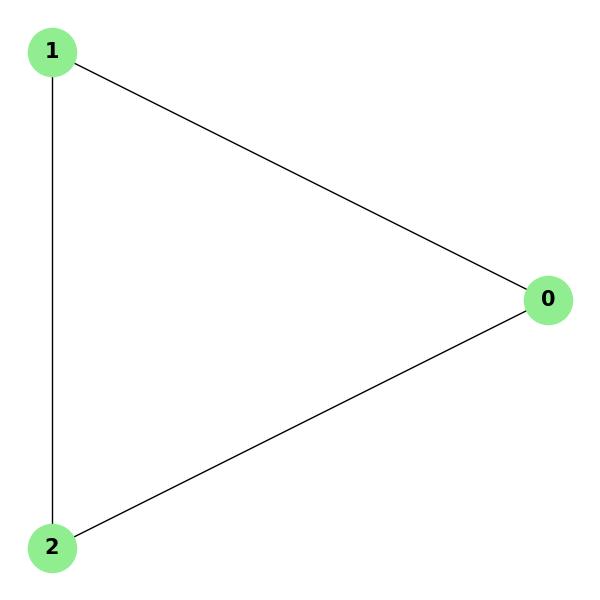
Example 1: A Planar Graph

Consider a simple triangular graph with 3 vertices and 3 edges. This graph is planar because it can be drawn on a plane without edge crossings. Additionally, Euler's formula holds −

Vertices (V): 3
Edges (E): 3
Faces (F): 2
Euler's formula: V - E + F = 3 - 3 + 2 = 2

Example 2: A Non-Planar Graph (K₅)

Consider the complete graph K₅, where all 5 vertices are connected. This graph is non-planar because it is impossible to draw without edge crossings. Kuratowski's Theorem confirms this by identifying K₅ as a forbidden subgraph.

Example 3: A Non-Planar Graph (K_3,3)

Consider the complete bipartite graph K_3,3. It is non-planar because it cannot be drawn without edge crossings. Kuratowski's Theorem identifies K_3,3 as a forbidden subgraph for planarity.

Applications of Planar Graphs

Planar graphs have several applications in various domains, they are −

Geographical Mapping: Planar graphs are used to represent regions and boundaries in maps without overlapping edges.
Circuit Design: In circuit design, planar graphs helps to minimize wire crossings, reducing complexity and improving efficiency.
Network Design: Planar graphs helps in designing communication networks with minimal interference.

Challenges in Determining Planarity

While Kuratowski's Theorem provides a strong method for determining planarity, there are still several challenges to consider −

Complex Graphs: Large and complex graphs require significant computational resources to identify subgraphs and test for planarity.
Subdivision Recognition: Identifying subdivisions of K₅ or K_3,3 within a graph can be tricky, especially for more complex graph structures.
Graph Reductions: Reducing the size of a graph for planarity testing while keeping its important features intact can be difficult.

Print Page