Graph Theory - Graph Products

---

---

Graph Products

In graph theory, graph products are operations that combine two or more graphs to produce a new graph. These products combine the structure of the original graphs in different ways, depending on the type of product used.

The resulting graph has properties derived from the original graphs, and the way the vertices and edges are combined is determined by the specific type of graph product.

In this tutorial, we will explore several types of graph products, their properties, construction methods, and applications.

Types of Graph Products

There are several types of graph products, each with different ways of combining two graphs. We will describe and explain each type in detail −

• Cartesian Product
• Direct Product
• Strong Product
• Lexicographic Product

Cartesian Product

The Cartesian product of two graphs G = (V_G, E_G) and H = (V_H, E_H) is a graph G H where the vertex set of G H is the Cartesian product of the vertex sets of G and H, and two vertices (g, h) and (g', h') are adjacent if and only if either −

• g = g' and hh' is an edge in H, or
• h = h' and gg' is an edge in G.

Formally, the Cartesian product G H can be written as −

V(G  H) = V_G  V_H
E(G  H) = {( (g, h), (g', h') ) | (g = g' and (h, h') ∈ E_H) or (h = h' and (g, g') ∈ E_G) }

This type of product produces a graph that has properties of both G and H and is used in applications such as parallel computation and network design.

Example of Cartesian Product

Consider the graphs G and H as shown below −

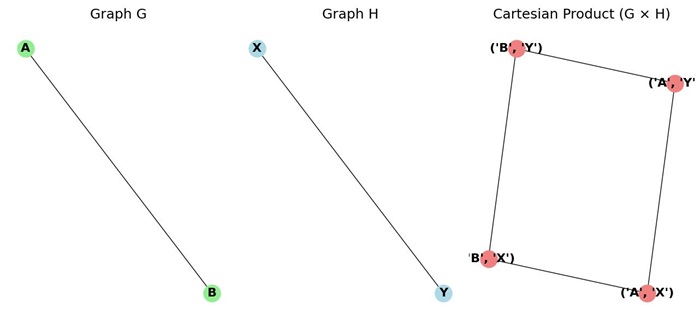
For the Cartesian product of these two graphs, each vertex in G H is a pair of vertices from G and H. Edges are formed by the rules specified earlier. This results in a new graph where the adjacency relationships are governed by the original graphs.

Direct Product

The direct product of two graphs G and H, denoted as G ⊗ H, is defined as a graph where the vertex set is the Cartesian product of the vertex sets of G and H, just like the Cartesian product. However, in the direct product, two vertices (g, h) and (g', h') are adjacent if and only if −

• gg' is an edge in G and hh' is an edge in H.

Formally, the direct product G ⊗ H can be written as −

V(G ⊗ H) = V_G  V_H
E(G ⊗ H) = {( (g, h), (g', h') ) | (g, g') ∈ E_G and (h, h') ∈ E_H }

The direct product tends to preserve more specific structures of the original graphs, making it useful for applications that require stricter interdependencies between the graphs.

The direct product is known with various other names. They are: tensor product, Kronecker product, cardinal product, relational product, cross product, conjunction, weak direct product, or categorical product.

Example of Direct Product

Consider the following two graphs G and H −

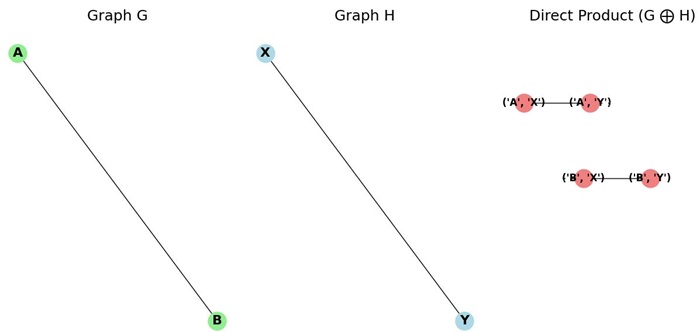
The direct product G ⊗ H produces a graph where the edges between the vertices are formed by the adjacency of both G and H independently.

Strong Product

The strong product of two graphs G and H, denoted G ⊙ H, is a graph where the vertex set is the same as the Cartesian product V_G V_H, and two vertices (g, h) and (g', h') are adjacent if −

• gg' is an edge in G and hh' is an edge in H (this condition holds as in the direct product), or
• gg' is an edge in G and h = h', or
• hh' is an edge in H and g = g'.

Formally, the strong product G ⊙ H can be written as −

V(G ⊙ H) = V_G  V_H
E(G ⊙ H) = {( (g, h), (g', h') ) | (g, g') ∈ E_G and (h, h') ∈ E_H or (g, g') ∈ E_G and h = h' or (h, h') ∈ E_H and g = g' }

This product combines both the Cartesian and direct product's properties, and it is used in cases where all combinations of adjacency relationships are important, such as in some types of routing problems.

Example of Strong Product

The following graph G and H demonstrate how the strong product combines both the Cartesian and direct product properties −

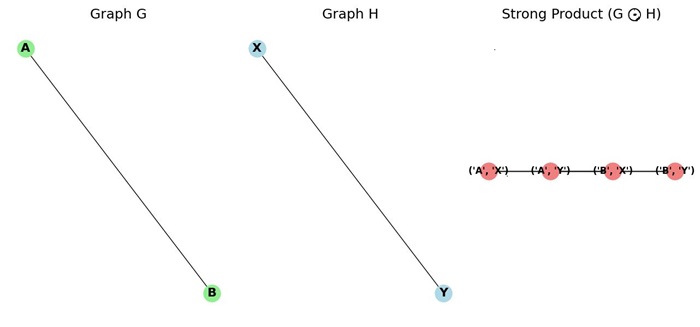
As shown in the image, the strong product G ⊙ H introduces additional edges based on the adjacency of vertices from both graphs.

Lexicographic Product

The lexicographic product of two graphs G and H, denoted G ∘ H, is a graph where the vertex set is the Cartesian product V_G V_H, and two vertices (g, h) and (g', h') are adjacent if −

• gg' is an edge in G, or
• g = g' and hh' is an edge in H.

Formally, the lexicographic product G ∘ H can be written as −

V(G ∘ H) = V_G  V_H
E(G ∘ H) = {( (g, h), (g', h') ) | (g, g') ∈ E_G or (g = g' and (h, h') ∈ E_H) }

The lexicographic product is useful in constructing graphs where one graph dominates the structure, and the other graph adds additional layers of connections.

Example of Lexicographic Product

Here is an example of the lexicographic product for the graphs G and H −

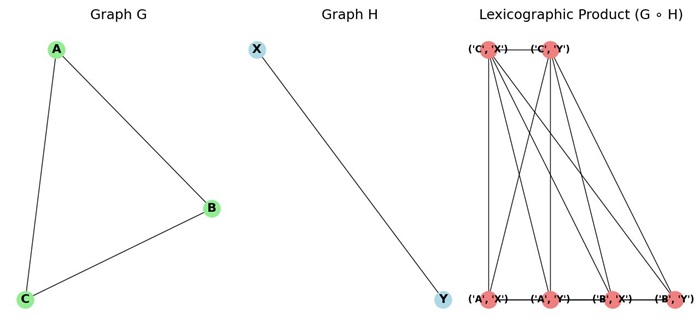
In the image, the lexicographic product G ∘ H connects vertices based on the adjacency relationships in both graphs.

Applications of Graph Products

Graph products have various applications in many fields, such as −

• Network Design: Graph products are used to design networks with specific topological properties by combining simple graph structures.
• Parallel Computing: Graph products can model parallel computation architectures where different tasks are interconnected.
• Distributed Systems: The analysis of distributed systems can be simplified by using graph products to represent the interconnections between system components.
• Quantum Computing: Some quantum computing problems are modeled using graph products, especially when dealing with entanglement and superposition.