Graph Theory - Graph Coloring

---

---

Graph Coloring

Graph coloring is a method of assigning labels or "colors" to the vertices or edges of a graph in such a way that no two adjacent vertices or edges share the same color.

The goal of graph coloring is to minimize the number of colors used, which is particularly useful in many real-world applications such as scheduling, resource allocation, and map coloring.

Types of Graph Coloring

There are mainly two types of graph coloring, they are −

• Vertex Coloring
• Edge Coloring

Vertex Coloring

In vertex coloring, the goal is to assign colors to the vertices of a graph so that no two adjacent vertices have the same color.

The smallest number of colors needed to color a graph is called the chromatic number of the graph.

For instance, in a graph with vertices A, B, and C where A is connected to B and B is connected to C, the vertex coloring would assign distinct colors to A, B, and C, ensuring that no two connected vertices share the same color −

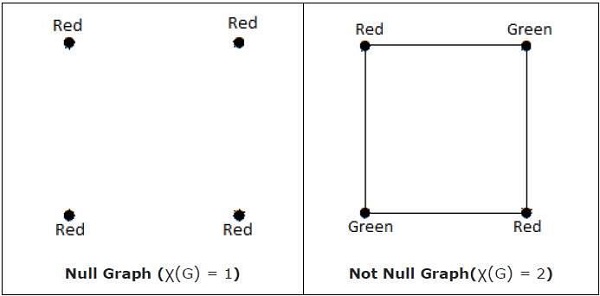
Edge Coloring

In edge coloring, the goal is to assign colors to the edges of a graph so that no two edges that share a common vertex have the same color.

For example, in a graph where edges connect vertices A and B, B and C, and A and C, edge coloring ensures that edges between A and B, and A and C are not assigned the same color −

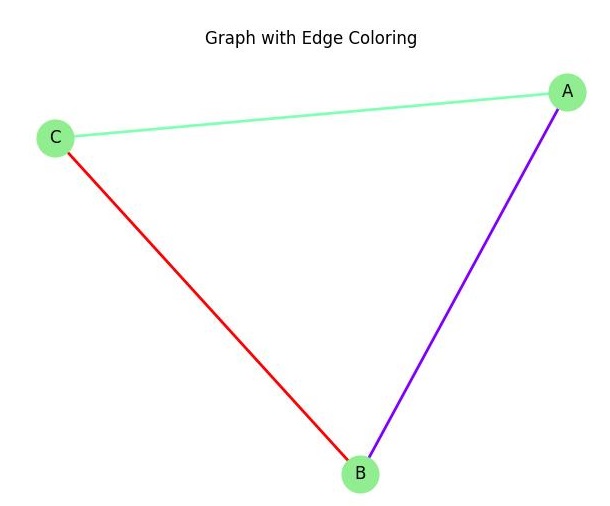
Applications of Graph Coloring

Graph coloring plays an important role in various real-life problems. Here are some examples −

• Map Coloring: The classic map coloring problem where regions of a map are colored in such a way that adjacent regions do not share the same color.
• Scheduling Problems: Graph coloring is used in scheduling where tasks are represented by vertices, and edges represent conflicts between tasks. The aim is to color the tasks so that conflicting tasks are not assigned the same time slot.
• Frequency Assignment: In telecommunications, graph coloring can be used to assign frequencies to transmitters so that no two adjacent transmitters use the same frequency.

Graph Coloring Problem

The graph coloring problem involves finding the minimum number of colors needed to color the vertices or edges of a graph while ensuring that adjacent vertices (or edges) do not share the same color. The minimum number of colors required to color a graph is called its chromatic number.

Chromatic Number

The chromatic number of a graph is the smallest number of colors required to color the vertices (or edges) such that no two adjacent vertices (or edges) share the same color. Finding the chromatic number is a well-known problem in graph theory and can be computationally difficult for large graphs.

For example, consider the following graph:

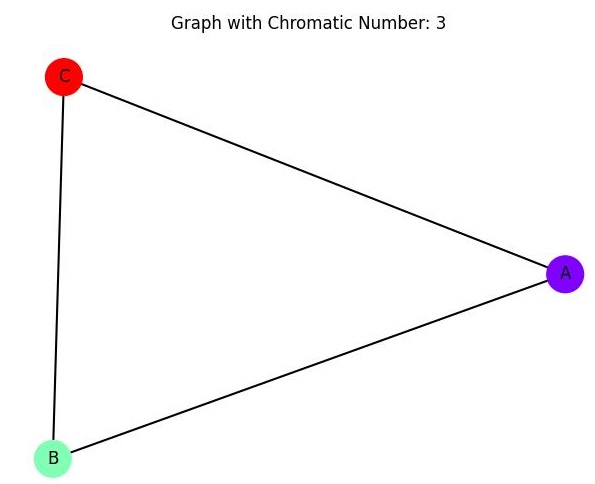
In this case, the chromatic number is 3 because we need at least 3 colors to color the graph such that no two adjacent vertices have the same color.

Graph Coloring Algorithms

There are several algorithms to find the chromatic number and color a graph. These include both exact and heuristic methods −

• Greedy Coloring Algorithm: A simple algorithm that colors the graph sequentially, assigning the first available color to each vertex.
• Backtracking Algorithm: A method that tries different colorings systematically and backtracks when an invalid coloring is encountered.
• DSATUR Algorithm: An approach that selects the vertex with the highest degree of saturation and colors it first.

Greedy Coloring Algorithm

The greedy algorithm colors the graph by visiting the vertices in a given order. For each vertex, it assigns the smallest available color that hasn't been used by any of its adjacent vertices. This method doesn't always provide the optimal solution but works well for many graphs.

Following are the steps for Greedy Coloring algorithm −

• Step 1: Order the vertices in a specific order (e.g., by degree, or randomly).
• Step 2: For each vertex, color it with the smallest available color that is not used by any of its neighbors.
• Step 3: Repeat the process until all vertices are colored.

Let us consider the following graph −

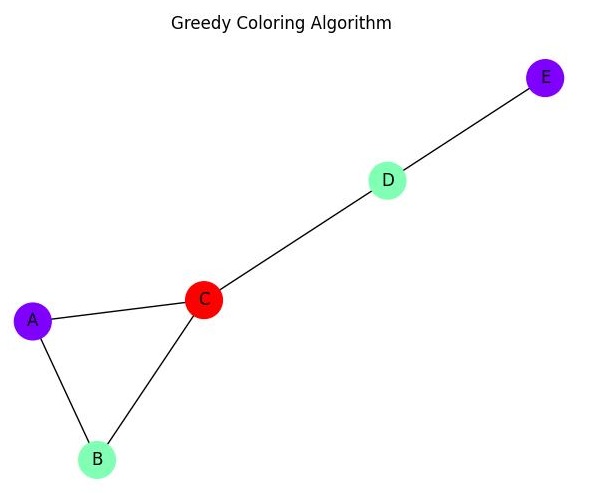
Using the greedy algorithm, we start by coloring the vertices. We first color vertex A with color 1. Then we color vertex B with color 2 because it's adjacent to A. We continue this process until all vertices are colored.

Backtracking Algorithm

Backtracking is an exact algorithm that explores all possible color assignments and backtracks when it encounters a coloring conflict. This method guarantees the optimal solution but is expensive for large graphs.

Following are the steps for Backtracking algorithm −

• Step 1: Try to color the first vertex with the first available color.
• Step 2: Move to the next vertex and try to assign the smallest available color.
• Step 3: If no valid color is available, backtrack and try a different color for the previous vertex.
• Step 4: Repeat the process until all vertices are colored.

Applications of Graph Coloring

One of the important applications of graph coloring is in scheduling problems. Imagine that you have a set of tasks that must be completed, and some tasks cannot be done at the same time due to resource conflicts. By treating tasks as vertices and conflicts as edges between them, you can use graph coloring to assign each task a time slot in such a way that no two conflicting tasks are assigned the same time slot.

Following are a few applications of graph coloring in real world problems −

• Scheduling: Assigning timeslots to exams in such a way that no two exams that share students have overlapping times.
• Network Frequency Assignment: Assigning frequencies to radio stations so that no two stations in close proximity interfere with each other.
• Map Coloring: Coloring regions of a map such that adjacent regions do not share the same color.

Example of Scheduling with Graph Coloring

Consider a set of tasks and their conflicts −

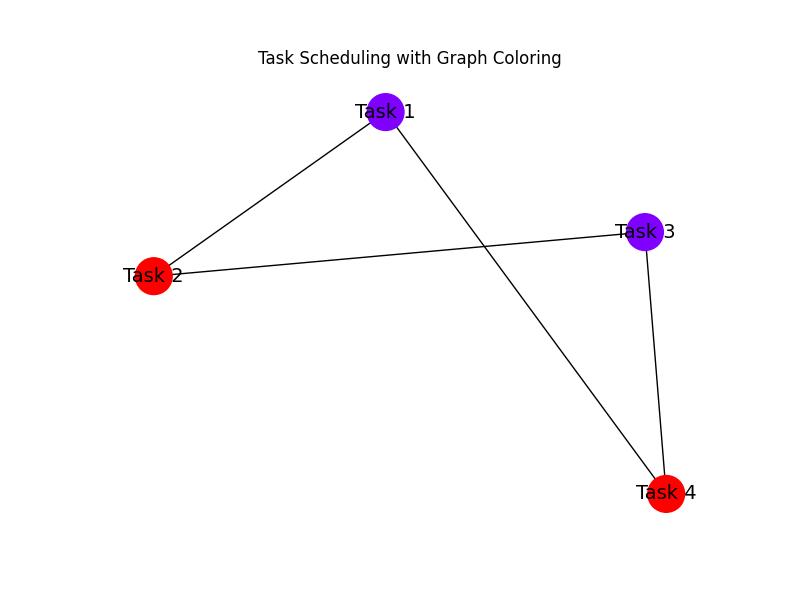
In this example, we used graph coloring to assign time slots to the tasks, ensuring that no two conflicting tasks are scheduled at the same time.