Graph Theory - Graph Labeling

---

---

Graph Labeling

Graph labeling is a mathematical concept where a graph's vertices, edges, or both are assigned labels (often numbers or symbols) according to specific rules or constraints.

These labels represents additional information, relationships, or properties of the graph and are used in various applications such as coding theory, network design, and data visualization.

The constraints in graph labeling vary depending on the specific type of labeling being used. Here are some common constraints associated with different labeling methods −

• Vertex Labeling: Each vertex is assigned a unique label or a label from a specific range.

• Edge Labeling: Each edge is assigned a label, often reflecting weights, capacities, or distances.

• Vertex-Edge Labeling: Both vertices and edges are labeled, with relationships between their labels. For example, in graceful labeling, the difference between the labels of two connected vertices is equal to the label of the edge joining them.

• Injective or Surjective Mappings: The labels may be required to form injective (unique mapping) or surjective (covering a range) mappings.

• Modulo Constraints: Labels may need to satisfy modular arithmetic rules (e.g., modular labeling).

• Additive or Multiplicative Constraints: The sum or product of labels of incident edges and vertices may need to satisfy a particular condition.

• Application-Specific Constraints: In coding theory, labels might need to minimize overlaps or collisions. In network design, labels might ensure non-interference in frequencies or paths.

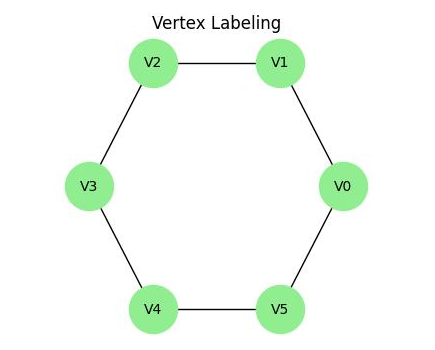
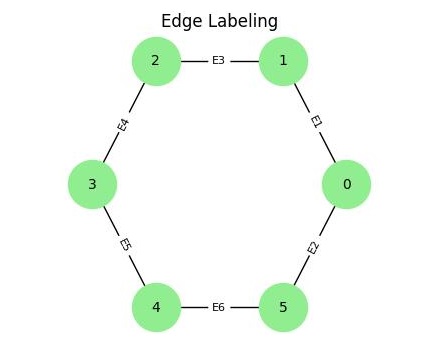
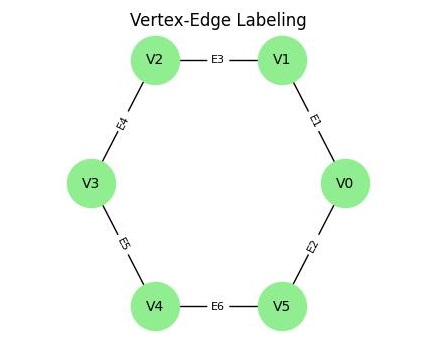
Types of Graph Labeling

Graph labeling can be categorized based on where the labels are applied (vertices or edges) and the constraints imposed on the labeling. There are several common types of graph labeling −

• Vertex Labeling: Labels are assigned to the vertices of the graph. The labeling satisfies certain properties, such as distinguishing adjacent vertices.
• Edge Labeling: Labels are assigned to the edges of the graph. Similar to vertex labeling, the labeling satisfies constraints such as distinguishing adjacent edges.
• Vertex-Edge Labeling: Labels are assigned to both vertices and edges of the graph simultaneously, with constraints on the relationships between vertex and edge labels.
• Total Labeling: This type assigns labels to both vertices and edges, ensuring that no two adjacent vertices or edges share the same label.

Graph Labeling Techniques

There are various techniques for labeling graphs based on the specific properties required by the problem at hand. Some of the most common techniques are −

Graceful Labeling

A graph is said to have a graceful labeling if it is possible to assign integers to the vertices of the graph such that the labels of adjacent vertices differ by exactly 1. This type of labeling is used in several applications, including error correction and network theory.

In graceful labeling, the vertices are assigned integers starting from 0 up to n-1, where n is the number of vertices in the graph. The edges are then assigned labels equal to the absolute difference of the labels of the adjacent vertices.

Example: Consider a simple graph with 3 vertices and 2 edges. The graceful labeling of this graph would look like −

Vertices: 0, 1, 2
Edges: (0, 1), (1, 2)
Edge Labels: |0-1| = 1, |1-2| = 1

Radio Labeling

Radio labeling is another technique where the labels are assigned to the vertices in such a way that the difference between the labels of adjacent vertices is greater than or equal to a certain threshold. The goal is to minimize the maximum label used in the labeling.

The objective of radio labeling is to find the smallest set of labels that satisfies the required distance condition, making it useful in scenarios like radio frequency assignment and signal processing.

Example: Consider a graph where we need to assign labels such that the difference in the labels of adjacent vertices is at least 2. In this case, the labels might look like −

Vertices: 0, 2, 4, 6

Edge Labeling

Edge labeling assigns labels to the edges of the graph rather than the vertices. The labeling can be done based on specific properties such as the distance between the labels of adjacent edges or ensuring no two edges incident to the same vertex have the same label.

Edge labeling has applications in designing communication networks, circuit design, and parallel processing, where each edge represents a different resource or connection.

Example: For a graph with edges labeled 1, 2, and 3, an edge labeling may look like −

Edge Labels: 1, 2, 3

Applications of Graph Labeling

Graph labeling techniques are used in various fields, especially where graph structures are involved in real-world applications. Following are some common areas where graph labeling is applied −

• Coding Theory: Graph labeling is applied in error-correcting codes, where labels are used to distinguish between different code words and ensure that they are separable under decoding conditions.
• Communication Networks: In wireless communication, radio labeling techniques are used to allocate frequencies to devices in a way that minimizes interference and ensures smooth communication.
• Scheduling Problems: Graph labeling is used in scheduling problems, where tasks are represented as vertices and edges represent dependencies. The goal is to assign resources to tasks in such a way that no two tasks share the same resource at the same time.
• Optimization: In resource allocation problems, graph labeling is used to assign resources to nodes or edges in a way that optimizes performance, such as minimizing cost or time.
• Network Design: In network design, graph labeling is used to assign labels to vertices or edges to optimize network connectivity and minimize resource usage.

Challenges in Graph Labeling

Although graph labeling is a powerful technique, it has several challenges −

• Computational Complexity: Determining the correct labeling, especially for large and complex graphs, can be expensive. Many graph labeling problems are NP-hard, meaning they are difficult to solve optimally in a reasonable amount of time.
• Uniqueness of Labeling: In many cases, there are multiple valid labelings possible for a graph, making it challenging to identify the most optimal or desirable labeling solution.
• Graph Size and Constraints: As the graph size increases, the constraints for labeling also increases. The larger the graph, the more complex the relationships between labels and the harder it becomes to find a solution that satisfies all constraints.

Example Problems in Graph Labeling

Let us look at some example problems to better understand graph labeling techniques −

Example 1: Graceful Labeling of a Path Graph

Consider a path graph with 5 vertices. The task is to find a graceful labeling for this graph. Since the graph is a path, it is possible to label the vertices with consecutive integers starting from 0 up to 4. The edge labels will be the absolute differences between adjacent vertices −

Vertices: 0, 1, 2, 3, 4
Edges: (0, 1), (1, 2), (2, 3), (3, 4)
Edge Labels: |0-1| = 1, |1-2| = 1, |2-3| = 1, |3-4| = 1

Example 2: Radio Labeling of a Cycle Graph

Consider a cycle graph with 4 vertices. We need to assign labels to the vertices such that the difference between adjacent vertices is at least 2. This problem requires finding the minimum labeling set that satisfies the condition −

Vertices: 0, 2, 4, 6