Graph Theory - Introduction

---

---

What is Graph Theory?

Graph theory is a branch of mathematics that studies graphs. Graphs are structures made up of points called vertices (or nodes) connected by lines called edges (or links). They model relationships between objects and are used in many fields to represent networks, relationships, and structures.

Formally, a graph is a pair of sets (V, E), where V is the set of vertices and E is the set of edges, connecting the pairs of vertices. Take a look at the following graph −

In the above graph,

V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de} 

History of Graph Theory

Graph theory dates back to the 18th century. Swiss mathematician Leonhard Euler is credited with founding graph theory in 1736 when he solved the Seven Bridges of Knigsberg problem.

Since then, graph theory has grown significantly, with contributions from many mathematicians, and is now widely used to solve modern problems.

Basic Definitions and Concepts

Here are some basic terms in graph theory −

• Vertex (Node): A fundamental unit representing a point or an object in a graph.
• Edge (Link): A line connecting two vertices, representing a relationship or pathway.
• Adjacent Vertices: Vertices connected by an edge.
• Degree of a Vertex: The number of edges connected to a vertex.
• Path: A sequence of vertices connected by edges, with each vertex visited only once.
• Cycle: A path that starts and ends at the same vertex, forming a loop.
• Connected Graph: A graph where there is a path between every pair of vertices.
• Subgraph: A graph made from a subset of vertices and edges of another graph.

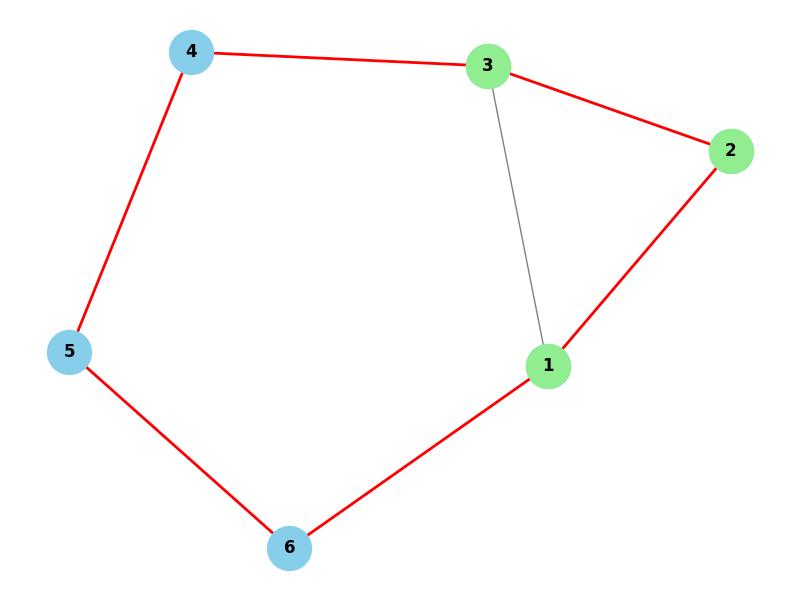
In this image,

• 1, 2, 3, 4, 5, 6 are the vertices (nodes) of the graph.
• The edges of the graph are represented by the pairs (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 1), and (1, 3), showing the connections between the vertices.
• Adjacent vertices are shown by the edges, such as 1 and 2, 2 and 3, 4 and 5, etc.
• The degree of a vertex is reflected in how many edges it is connected to, for example, vertex 1 has a degree of 2.
• A path is represented by a continuous sequence of edges, such as 1 2 3 4 5 6 1.
• A cycle is illustrated by the loop 1 2 3 4 5 6 1.
• The graph is connected, meaning every vertex is reachable from any other vertex.
• The subgraph, consisting of vertices 1, 2, and 3, is a smaller portion of the original graph.

Types of Graphs

Graphs can be classified into different types −

• Undirected Graph: A graph where edges have no direction, meaning connections are bidirectional.
• Directed Graph (Digraph): A graph where edges have a direction, indicating one-way relationships between vertices.
• Weighted Graph: A graph where edges have weights or costs, representing the strength or capacity of connections.
• Unweighted Graph: A graph where all edges are equal, with no weights assigned.
• Simple Graph: A graph with no loops (edges connecting a vertex to itself) and no multiple edges between the same vertices.
• Multigraph: A graph that allows multiple edges between the same vertices.
• Bipartite Graph: A graph whose vertices can be divided into two sets where no two vertices within the same set are adjacent.
• Complete Graph: A graph where there is an edge between every pair of vertices.

Graph Representation

Graphs can be represented in various ways −

• Adjacency Matrix: A square matrix where the element at row i and column j indicates the presence of an edge between vertices i and j.
• Adjacency List: A collection of lists where each list contains the vertices adjacent to a particular vertex.
• Incidence Matrix: A matrix where rows represent vertices and columns represent edges, showing which vertices are connected by which edges.

In this image,

Adjacency List:
1: [2]
2: [1, 3]
3: [2, 4]
4: [3, 5]
5: [4]

Adjacency Matrix:
[[0. 1. 0. 0. 0.]
 [1. 0. 1. 0. 0.]
 [0. 1. 0. 1. 0.]
 [0. 0. 1. 0. 1.]
 [0. 0. 0. 1. 0.]]

Incidence Matrix:
[[1. 0. 0. 0.]
 [1. 1. 0. 0.]
 [0. 1. 1. 0.]
 [0. 0. 1. 1.]
 [0. 0. 0. 1.]]

Graph Algorithms

Graph theory includes many algorithms for solving graph-related problems −

• Depth-First Search (DFS): An algorithm for exploring a graph by going as deep as possible along each branch before backtracking.
• Breadth-First Search (BFS): An algorithm for exploring a graph by visiting all vertices at the current depth before moving deeper.
• Dijkstra's Algorithm: An algorithm for finding the shortest paths between vertices in a weighted graph.
• Prim's Algorithm: An algorithm for finding a minimum spanning tree in a weighted, connected graph.
• Kruskal's Algorithm: An algorithm for finding a minimum spanning tree by adding edges in increasing weight order.
• Floyd-Warshall Algorithm: An algorithm for finding shortest paths between all pairs of vertices in a weighted graph.

Importance of Graph Theory

Graph theory is important because it helps analyze and solve complex problems involving relationships and interactions.

By representing problems as graphs, we can use mathematical tools to find efficient solutions. Graph theory helps us understand the structure of networks and systems, aiding in decision-making in various fields.

Learning Graph Theory

Learning graph theory involves studying its basic concepts, definitions, and theorems, and exploring its applications through examples and exercises.

A strong foundation in graph theory allows you to apply its principles to real-world problems and contribute to advances in science, technology, and mathematics.