Graph Theory - Directed Graphs

---

---

Directed Graph

A directed graph (or digraph) is a graph where each edge has a direction, indicating the relationship between two vertices. In a directed graph, the edges are ordered pairs, meaning the edges go from one vertex (the tail) to another vertex (the head).

In contrast to an undirected graph, where edges are bidirectional, a directed graph has directed edges, and the direction matters in many real-life applications like routing, flow systems, and dependency graphs.

Directed graphs are widely used in network routing, task scheduling, state transitions, and resource allocation, where the direction of relationships or processes is important.

This tutorial will explore the various components, representations, properties, and applications of directed graphs.

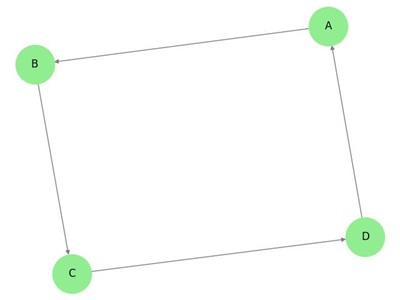
Example

Consider a directed graph with vertices V = {A, B, C, D} and edges E = {(A B), (B C), (C D), (D A)}. This is a directed graph because −

• The edges have a direction (for example, A B means the edge starts at vertex A and ends at vertex B).
• The direction of each edge is important, and it determines the flow of information, control, or dependencies.

Representation of Directed Graphs

Directed graphs can be represented in multiple ways depending on the application and the level of detail required. The most common representations include adjacency matrices, adjacency lists, and edge lists.

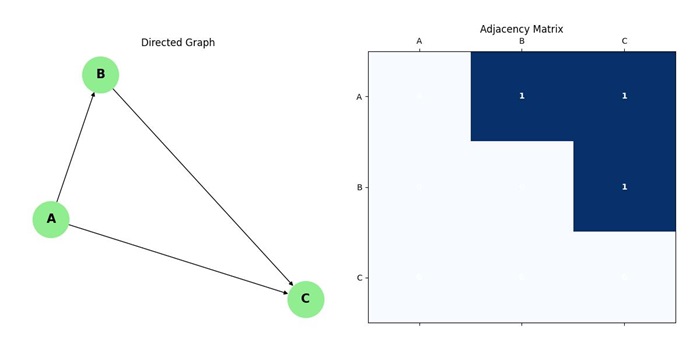
Adjacency Matrix Representation

The adjacency matrix of a directed graph is a square matrix where each entry a[i][j] indicates whether there is a directed edge from vertex i to vertex j. In the matrix, 1 indicates the presence of a directed edge, and 0 indicates the absence of one.

Example

For the directed graph with vertices V = {A, B, C} and edges E = {(A B), (B C), (A C)}, the adjacency matrix would look like this −

	A	B	C
A	0	1	1
B	0	0	1
C	0	0	0

This matrix indicates −

• There is a directed edge from A B.
• There is a directed edge from B C.
• There is a directed edge from A C.
• There are no edges starting or ending at C.

Adjacency List Representation

The adjacency list representation is a more space-efficient way to represent a directed graph. Each vertex has a list of its adjacent vertices, representing the direction of the edges.

Example

For the directed graph with vertices V = {A, B, C} and edges E = {(A B), (B C), (A C)}, the adjacency list representation would be −

• A: [B, C]
• B: [C]
• C: []

Here, vertex A points to B and C, while vertex B points to C, and vertex C has no outgoing edges.

Edge List Representation

In the edge list representation, each directed edge is simply represented as a pair of vertices, indicating the direction of the edge.

Example

For the directed graph with edges E = {(A B), (B C), (A C)}, the edge list representation would be −

• (A B)
• (B C)
• (A C)

Degree of a Vertex in Directed Graphs

The degree of a vertex in a directed graph is broken down into two parts: the in-degree and out-degree.

In-degree

The in-degree of a vertex is the number of edges that point to that vertex. It represents the number of incoming edges to the vertex.

Example

For the directed graph with edges E = {(A B), (B C), (A C)}, the in-degree of each vertex is −

• deg_in(A) = 0 (no edges point to A)
• deg_in(B) = 1 (one edge points to B: A B)
• deg_in(C) = 2 (two edges point to C: B C and A C)

Out-degree

The out-degree of a vertex is the number of edges that originate from that vertex. It represents the number of outgoing edges from the vertex.

Example

For the directed graph with edges E = {(A B), (B C), (A C)}, the out-degree of each vertex is −

• deg_out(A) = 2 (edges A B and A C)
• deg_out(B) = 1 (edge B C)
• deg_out(C) = 0 (no outgoing edges)

Properties of Directed Graphs

Directed graphs have unique properties that distinguish them from undirected graphs. These properties are important in understanding the structure and behavior of directed graphs in different applications.

Transitivity

In a directed graph, if there is a directed edge from vertex A to vertex B and from vertex B to vertex C, the graph is said to be transitive if there is a direct edge from vertex A to vertex C.

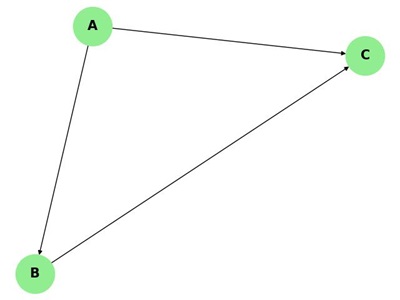
Strongly Connected Graph

A directed graph is said to be strongly connected if there is a directed path from every vertex to every other vertex. In other words, there is a way to travel from any vertex to any other vertex by following the directed edges.

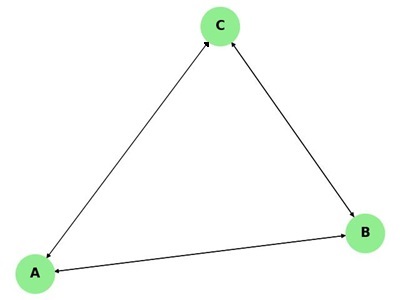
Weakly Connected Graph

A directed graph is weakly connected if replacing all directed edges with undirected edges results in a connected graph. In a weakly connected graph, there may not be a directed path between every pair of vertices, but there is a way to connect them by disregarding the direction of edges.

Acyclic Graph

A directed graph is acyclic if it does not contain any directed cycles, i.e., there is no path that starts and ends at the same vertex, following the directions of the edges. Directed acyclic graphs (DAGs) are important in applications like task scheduling, dependency resolution, and data processing.

Rooted Directed Graph

A directed graph is said to be rooted if there is a special vertex, called the root, from which all other vertices can be reached by following the directed edges.

Applications of Directed Graphs

Directed graphs are used in various fields, including computer science, biology, social networks, and more. Their ability to represent relationships with direction makes them versatile for various applications.

Computer Networks

In computer networks, directed graphs are used to model network topology, where vertices represent routers or computers, and directed edges represent communication links between them. Routing algorithms such as Dijkstras algorithm operate on directed graphs to find the shortest paths between nodes.

Task Scheduling

In task scheduling, directed acyclic graphs (DAGs) are used to represent dependencies between tasks. The vertices represent tasks, and the directed edges represent dependency relationships, indicating which tasks must be completed before others can start.

Social Networks

In social network analysis, directed graphs are used to model relationships between users. For example, in Twitter, a directed graph can represent followers, where the directed edge from A to B indicates that A is following B.

Web Page Link Structure

Directed graphs are used to represent the structure of the web, where vertices are web pages and directed edges represent hyperlinks from one page to another. This structure is important in search engine algorithms like PageRank, which determines the importance of a web page based on its incoming links.