
- Graph Theory - Home
- Graph Theory - Introduction
- Graph Theory - History
- Graph Theory - Fundamentals
- Graph Theory - Applications
- Types of Graphs
- Graph Theory - Types of Graphs
- Graph Theory - Simple Graphs
- Graph Theory - Multi-graphs
- Graph Theory - Directed Graphs
- Graph Theory - Weighted Graphs
- Graph Theory - Bipartite Graphs
- Graph Theory - Complete Graphs
- Graph Theory - Subgraphs
- Graph Theory - Trees
- Graph Theory - Forests
- Graph Theory - Planar Graphs
- Graph Theory - Hypergraphs
- Graph Theory - Infinite Graphs
- Graph Theory - Random Graphs
- Graph Representation
- Graph Theory - Graph Representation
- Graph Theory - Adjacency Matrix
- Graph Theory - Adjacency List
- Graph Theory - Incidence Matrix
- Graph Theory - Edge List
- Graph Theory - Compact Representation
- Graph Theory - Incidence Structure
- Graph Theory - Matrix-Tree Theorem
- Graph Properties
- Graph Theory - Basic Properties
- Graph Theory - Coverings
- Graph Theory - Matchings
- Graph Theory - Independent Sets
- Graph Theory - Traversability
- Graph Theory Connectivity
- Graph Theory - Connectivity
- Graph Theory - Vertex Connectivity
- Graph Theory - Edge Connectivity
- Graph Theory - k-Connected Graphs
- Graph Theory - 2-Vertex-Connected Graphs
- Graph Theory - 2-Edge-Connected Graphs
- Graph Theory - Strongly Connected Graphs
- Graph Theory - Weakly Connected Graphs
- Graph Theory - Connectivity in Planar Graphs
- Graph Theory - Connectivity in Dynamic Graphs
- Special Graphs
- Graph Theory - Regular Graphs
- Graph Theory - Complete Bipartite Graphs
- Graph Theory - Chordal Graphs
- Graph Theory - Line Graphs
- Graph Theory - Complement Graphs
- Graph Theory - Graph Products
- Graph Theory - Petersen Graph
- Graph Theory - Cayley Graphs
- Graph Theory - De Bruijn Graphs
- Graph Algorithms
- Graph Theory - Graph Algorithms
- Graph Theory - Breadth-First Search
- Graph Theory - Depth-First Search (DFS)
- Graph Theory - Dijkstra's Algorithm
- Graph Theory - Bellman-Ford Algorithm
- Graph Theory - Floyd-Warshall Algorithm
- Graph Theory - Johnson's Algorithm
- Graph Theory - A* Search Algorithm
- Graph Theory - Kruskal's Algorithm
- Graph Theory - Prim's Algorithm
- Graph Theory - Borůvka's Algorithm
- Graph Theory - Ford-Fulkerson Algorithm
- Graph Theory - Edmonds-Karp Algorithm
- Graph Theory - Push-Relabel Algorithm
- Graph Theory - Dinic's Algorithm
- Graph Theory - Hopcroft-Karp Algorithm
- Graph Theory - Tarjan's Algorithm
- Graph Theory - Kosaraju's Algorithm
- Graph Theory - Karger's Algorithm
- Graph Coloring
- Graph Theory - Coloring
- Graph Theory - Edge Coloring
- Graph Theory - Total Coloring
- Graph Theory - Greedy Coloring
- Graph Theory - Four Color Theorem
- Graph Theory - Coloring Bipartite Graphs
- Graph Theory - List Coloring
- Advanced Topics of Graph Theory
- Graph Theory - Chromatic Number
- Graph Theory - Chromatic Polynomial
- Graph Theory - Graph Labeling
- Graph Theory - Planarity & Kuratowski's Theorem
- Graph Theory - Planarity Testing Algorithms
- Graph Theory - Graph Embedding
- Graph Theory - Graph Minors
- Graph Theory - Isomorphism
- Spectral Graph Theory
- Graph Theory - Graph Laplacians
- Graph Theory - Cheeger's Inequality
- Graph Theory - Graph Clustering
- Graph Theory - Graph Partitioning
- Graph Theory - Tree Decomposition
- Graph Theory - Treewidth
- Graph Theory - Branchwidth
- Graph Theory - Graph Drawings
- Graph Theory - Force-Directed Methods
- Graph Theory - Layered Graph Drawing
- Graph Theory - Orthogonal Graph Drawing
- Graph Theory - Examples
- Computational Complexity of Graph
- Graph Theory - Time Complexity
- Graph Theory - Space Complexity
- Graph Theory - NP-Complete Problems
- Graph Theory - Approximation Algorithms
- Graph Theory - Parallel & Distributed Algorithms
- Graph Theory - Algorithm Optimization
- Graphs in Computer Science
- Graph Theory - Data Structures for Graphs
- Graph Theory - Graph Implementations
- Graph Theory - Graph Databases
- Graph Theory - Query Languages
- Graph Algorithms in Machine Learning
- Graph Neural Networks
- Graph Theory - Link Prediction
- Graph-Based Clustering
- Graph Theory - PageRank Algorithm
- Graph Theory - HITS Algorithm
- Graph Theory - Social Network Analysis
- Graph Theory - Centrality Measures
- Graph Theory - Community Detection
- Graph Theory - Influence Maximization
- Graph Theory - Graph Compression
- Graph Theory Real-World Applications
- Graph Theory - Network Routing
- Graph Theory - Traffic Flow
- Graph Theory - Web Crawling Data Structures
- Graph Theory - Computer Vision
- Graph Theory - Recommendation Systems
- Graph Theory - Biological Networks
- Graph Theory - Social Networks
- Graph Theory - Smart Grids
- Graph Theory - Telecommunications
- Graph Theory - Knowledge Graphs
- Graph Theory - Game Theory
- Graph Theory - Urban Planning
- Graph Theory Useful Resources
- Graph Theory - Quick Guide
- Graph Theory - Useful Resources
- Graph Theory - Discussion
Graph Theory - Chordal Graphs
Chordal Graphs
A chordal graph, also known as a "perfectly triangulated graph," is a special type of graph where every cycle of length greater than 3 contains a chord. A chord is defined as an edge that connects two non-adjacent vertices within the cycle.
Chordal graphs are important in graph theory due to their structural properties and the fact that they allow efficient algorithms for various graph problems.
The following image shows an example of a chordal graph −
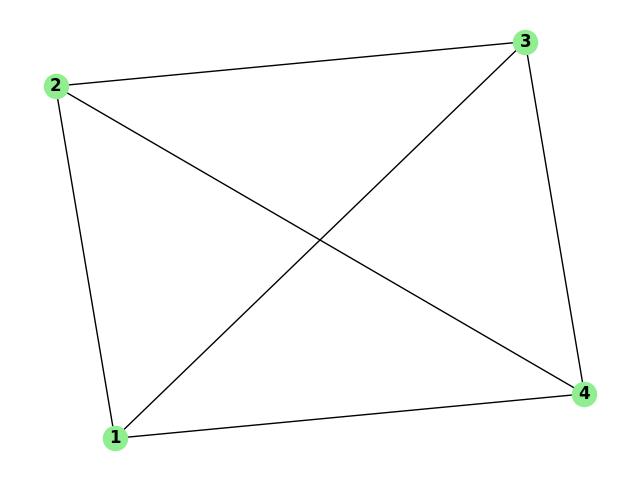
Properties of Chordal Graphs
Chordal graphs have several unique properties that distinguish them from other types of graphs. Some of these properties are −
- Perfect Elimination Ordering: Chordal graphs allow for a perfect elimination ordering, which is a sequence of vertices such that each vertex has all its neighbors from earlier in the ordering.
- Cliques: A maximal clique in a chordal graph is a subset of vertices that forms a clique (every vertex is connected to every other vertex in the subset) and cannot be extended by adding an adjacent vertex.
- Cycle Condition: Any cycle in the graph with more than 3 vertices must have a chord, which ensures that the graph has a more rigid structure than non-chordal graphs.
- Planarity: Chordal graphs may or may not be planar, meaning they can either be drawn on a flat plane without any edges crossing or require the use of additional dimensions to be drawn without crossings. However, many chordal graphs used in practical problems are planar.
- Graph Decomposition: Chordal graphs can be decomposed into cliques using algorithms like clique tree decomposition. This makes them useful in optimization problems.
Chordal graphs are useful in computer science, especially for solving problems like graph coloring, clique problems, and optimization tasks.
Classification of Chordal Graphs
Chordal graphs can be classified into various subtypes based on their structure and properties. These classifications are −
- Triangulated Graph: A triangulated graph is another name for a chordal graph, where each cycle of length greater than 3 contains a chord.
- Interval Graph: An interval graph is a type of chordal graph where each vertex corresponds to an interval on a line, and edges represent overlap between intervals.
- Split Graph: A split graph is a chordal graph that can be divided into two sets of vertices: one set that forms a clique (i.e., all vertices in this set are connected to each other) and the other set that forms an independent set (i.e., no vertices in this set are connected to each other).
- Packing Graph: A packing graph is a chordal graph where the vertices can be assigned to "packing" regions, such as in geometric problems.
Applications of Chordal Graphs
Chordal graphs have various applications in computer science and optimization problems, such as −
- Graph Coloring: Chordal graphs are used in graph coloring algorithms. A coloring problem involves assigning colors to the vertices of a graph such that no two adjacent vertices share the same color. The structure of chordal graphs makes this task easier, especially in scheduling problems and resource allocation.
- Perfect Elimination Orderings: The concept of perfect elimination orderings in chordal graphs is useful in various algorithms, such as those used for finding cliques in large networks, decomposing graphs, and solving constraint satisfaction problems.
- Optimization Problems: Chordal graphs are used in solving linear programming problems, as well as in various optimization tasks.
- Biological Networks: Chordal graphs are used to model interactions within biological networks, such as protein-protein interaction networks. Their ability to identify cliques and manage complex interactions makes them valuable in the study of biological systems and diseases.
Testing Chordality in Graphs
There are various methods to test whether a graph is chordal, such as −
- Perfect Elimination Ordering: If a graph allows for a perfect elimination ordering, it is chordal.
- Cycle Condition: Testing whether every cycle of length greater than 3 contains a chord is another way to check for chordality.
Various Types of Chordal Graphs
There are several special types of chordal graphs that exhibit unique properties. The following table summarizes some of the most common types of chordal graphs −
| Graph Type | Notes |
|---|---|
| Triangulated Graph | A triangulated graph is a chordal graph in which every cycle of length greater than 3 has a chord, ensuring no cycles without chords. |
| Interval Graph | An interval graph is a chordal graph where vertices represent intervals, and edges represent overlaps between intervals. |
| Split Graph | A split graph is a chordal graph that can be divided into two sets, one of which forms a clique and the other an independent set. |
| Packing Graph | A packing graph is a chordal graph where vertices correspond to regions in a packing problem, with edges indicating the interaction between regions. |
| Perfect Graph | A perfect graph is a chordal graph where the chromatic number of every induced subgraph equals the size of the largest clique in that subgraph. This property is used in advanced graph theory problems involving coloring and clique finding. |
| Complete Graph | A complete graph is trivially chordal, as every cycle of length greater than 3 contains multiple chords connecting vertices. |