Graph Theory - Basic Properties

---

---

Graph Properties

In graph theory, the basic properties of a graph help us understand its structure and behaviour. These properties provide details of how vertices and edges are related, which can be used to solve practical problems in computer science, engineering, and social networks.

In this chapter, we will explore the fundamental properties of graphs, such as connectivity, degree, and more.

Types of Graphs

Graphs can have various types based on the edges and vertices they contain. Some of the common types of graphs are −

• Undirected Graph: A graph in which edges have no direction. The edges represent a two-way relationship between vertices.

• Directed Graph (Digraph): A graph in which edges have a direction, indicating a one-way relationship between vertices.

• Weighted Graph: A graph in which edges have weights or costs associated with them, usually representing distances, time, or other quantities.

• Complete Graph: A graph in which every pair of distinct vertices is connected by a unique edge.

• Tree: A connected graph with no cycles, where there is exactly one path between any two vertices.

• Multigraph: A graph that allows multiple edges between two vertices.

• Planar Graph: A graph that can be drawn on a plane without any edges crossing.

Basic Terminology

To understand graph properties, it is important to familiarize ourselves with basic graph properties terminology −

• Vertex: A node in the graph that represents an entity, such as a city, computer, or person.
• Edge: A connection between two vertices, representing a relationship between them.
• Degree of a Vertex: The number of edges incident to a vertex. In an undirected graph, it is the number of edges connected to that vertex. In a directed graph, it is divided into in-degree (edges directed towards the vertex) and out-degree (edges directed away from the vertex).
• Adjacent Vertices: Two vertices are adjacent if there is an edge connecting them.
• Path: A sequence of vertices connected by edges.
• Cycle: A path that starts and ends at the same vertex without repeating any edges or vertices.
• Connected Graph: A graph in which there is a path between every pair of vertices.
• Subgraph: A graph formed from a subset of the vertices and edges of another graph.

Degree of a Vertex

The degree of a vertex is an important property that gives us information about the vertex's connectivity within a graph. There are two types of degree −

• Indegree: In a directed graph, the indegree of a vertex is the number of incoming edges (edges directed towards the vertex).
• Outdegree: In a directed graph, the outdegree of a vertex is the number of outgoing edges (edges directed away from the vertex).
• Degree (Undirected Graph): In an undirected graph, the degree of a vertex is the total number of edges incident to that vertex.

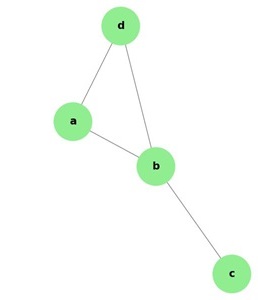
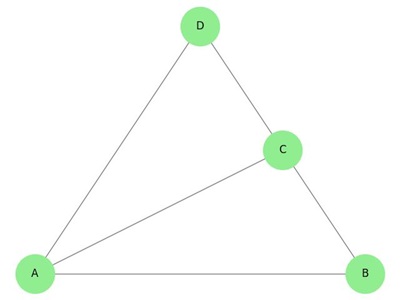
Consider the following undirected graph −

The degree of vertex "a" is 2, since there are two edges connected to vertex "a" (a-b and a-d).

Connectivity

Connectivity is a fundamental property of graphs that describes how vertices are related. A graph can be classified into different types of connectivity −

• Connected Graph: A graph is connected if there is a path between any pair of vertices in the graph.
• Disconnected Graph: A graph is disconnected if there exists at least one pair of vertices with no path between them.
• Strongly Connected (Directed Graph): In a directed graph, the graph is strongly connected if there is a directed path from every vertex to every other vertex.
• Weakly Connected (Directed Graph): A directed graph is weakly connected if there is a path between every pair of vertices, ignoring the direction of edges.

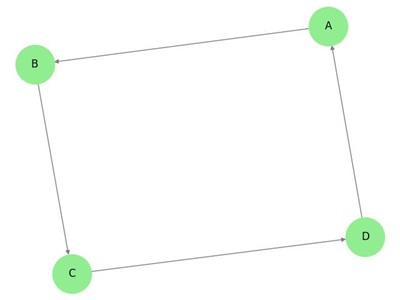
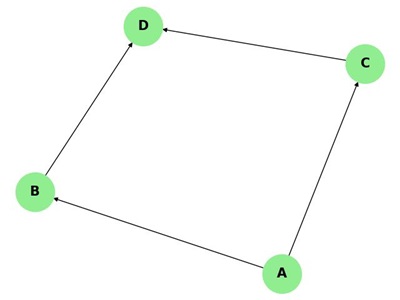
Consider the following directed graph −

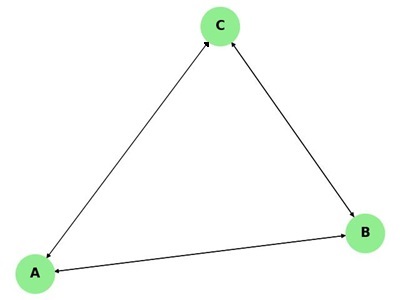
This graph is strongly connected because there is a directed path between every pair of vertices. If we ignore the direction of edges, the graph becomes weakly connected.

Graph Diameter and Radius

The diameter and radius of a graph provide information about the "spread" of the graph −

• Diameter of a Graph: The diameter is the greatest distance (in terms of edges) between any two vertices in the graph. It is the longest shortest path between any pair of vertices.
• Radius of a Graph: The radius is the minimum distance from any vertex to all other vertices in the graph. It is the center of the graph.

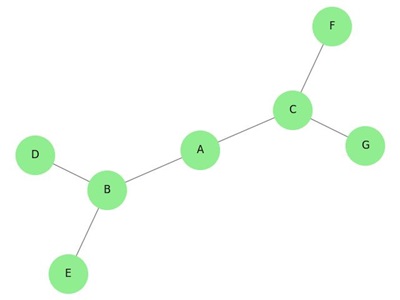
Consider the following simple graph −

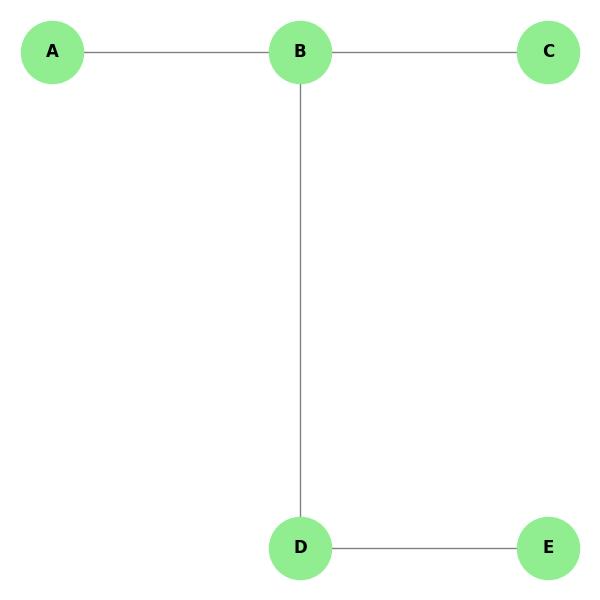
The diameter of this graph is 3, as the longest shortest path is from vertex A to vertex C (A B C). The radius is 2, as vertex B has the shortest distance to all other vertices (B A, B C, B D, B E).

Cycle and Acyclic Graphs

A cycle represents a path that starts and ends at the same vertex without revisiting any vertex more than once. A graph can be classified based on its cycles −

• Cyclic Graph: A graph that contains at least one cycle.

• Acyclic Graph: A graph that contains no cycles. A tree is an example of an acyclic graph.

• Directed Acyclic Graph (DAG): A directed graph that contains no cycles, meaning there is no directed path from a vertex to itself.

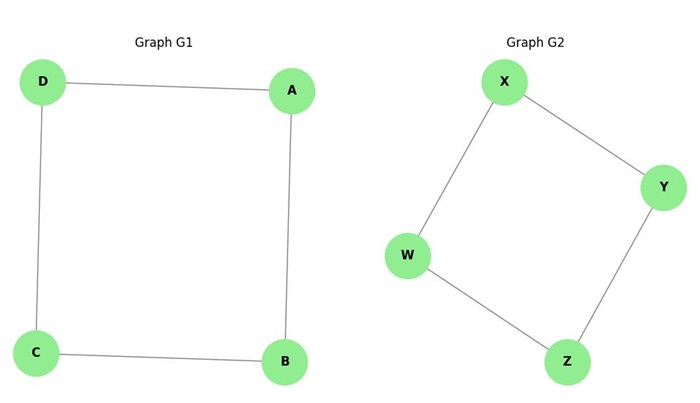
Isomorphism

Graph isomorphism refers to two graphs being equivalent in terms of structure, even if they may look different visually. Two graphs G₁ and G₂ are said to be isomorphic if there is a one-to-one correspondence between their vertices and edges, preserving adjacency.

Graph isomorphism is useful in various applications, such as pattern recognition, molecular chemistry, and network theory.

Subgraphs

A subgraph is a portion of a graph that includes a subset of the vertices and edges of the original graph.

There are two main types of subgraphs −

• Induced Subgraph: A subgraph formed by a subset of vertices and all edges that connect pairs of these vertices in the original graph.

• Spanning Subgraph: A subgraph that includes all the vertices of the original graph.

Graph Complements

The complement of a graph G is a graph G' that contains exactly the edges that are not in G, while keeping the same set of vertices. The complement graph is useful for understanding the relationships between non-adjacent vertices.

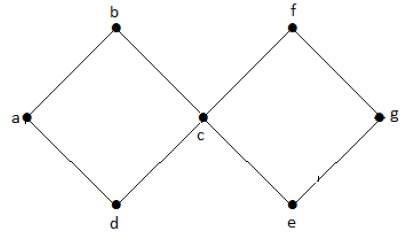
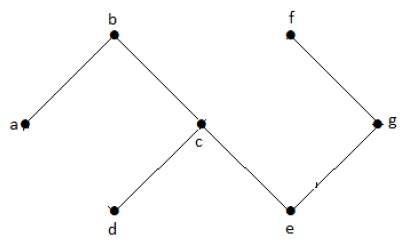
Distance between Two Vertices

The distance between two vertices in a graph is the number of edges in the shortest path between them. If there are multiple paths connecting two vertices, the shortest path is considered as the distance between them. It is denoted as −

d(U, V)

For example, take a look at the following graph −

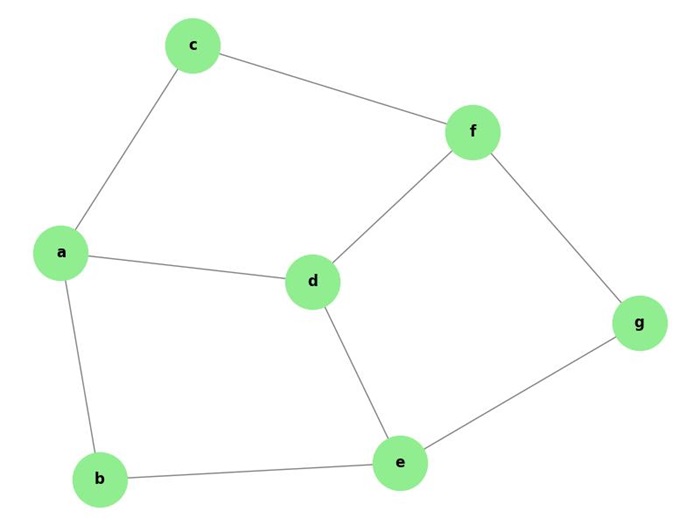
In the given graph, consider two vertices 'd' and 'e'. The distance between these vertices, denoted as 'de', is 1 because there is a direct edge connecting them. However, there are multiple possible paths from vertex 'd' to vertex 'e'. Some of these paths are −

da, ab, be
df, fg, ge
de (direct edge)
df, fc, ca, ab, be
da, ac, cf, fg, ge

In this case, the shortest path 'de' is considered for the distance.

Eccentricity of a Vertex

The eccentricity of a vertex is defined as the maximum distance from that vertex to all other vertices in the graph. It helps in identifying the "farthest" vertex from a given vertex. It is denoted as −

e(V)

For example, consider the eccentricity of vertex 'a' in the above given graph −

The distance from 'a' to 'b' is 1 ('ab').
The distance from 'a' to 'c' is 1 ('ac').
The distance from 'a' to 'd' is 1 ('ad').
The distance from 'a' to 'e' is 2 ('ab'  'be' or 'ad'  'de').
The distance from 'a' to 'f' is 2 ('ac'  'cf' or 'ad'  'df').
The distance from 'a' to 'g' is 3 ('ac'  'cf'  'fg' or 'ad'  'df'  'fg').

Thus, the eccentricity of vertex 'a' is 3, as it is the maximum distance from 'a' to any other vertex.

Central Point

A central point in a graph is a vertex whose eccentricity is equal to the radius of the graph. In other words, the central point is the vertex with the minimum maximum distance to all other vertices.

In the above example graph, vertex 'd' is the central point as its eccentricity equals the radius (e(d) = r(d) = 2).

Centre of the Graph

The set of all central points of a graph is called the centre of the graph. These points are important for identifying vertices that are "equidistant" from all other vertices in the graph.

In the above example graph, the centre is {'d'}, which is the only central point.

Circumference of a Graph

The circumference of a graph is defined as the number of edges in the longest cycle within the graph. It represents the longest closed loop or cycle in the graph.

For the above example graph, the circumference is 6, which can be derived from the longest cycle, such as a-c-f-g-e-b-a or a-c-f-d-e-b-a.

Girth of a Graph

The girth of a graph is the number of edges in the shortest cycle of the graph. It measures the "smallest" closed loop present in the graph. It is denoted as −

g(G)

For the above given example graph, the girth is 4, which can be derived from the shortest cycle, such as a-c-f-d-a, d-f-g-e-d, or a-b-e-d-a.

Sum of Degrees of Vertices Theorem

For a non-directed graph G = (V, E), where V is the set of vertices and E is the set of edges, the sum of degrees of all vertices is twice the number of edges −

n  i=1 deg(Vi) = 2|E|

Corollary 1: For a directed graph G = (V, E), the sum of the out-degrees equals the sum of the in-degrees, which is equal to the number of edges −

n  i=1 deg+(Vi) = |E| = n  i=1 deg-(Vi)

Corollary 2: In any non-directed graph, the number of vertices with an odd degree is always even.

Corollary 3: If the degree of each vertex in a non-directed graph is k, then −

k|V| = 2|E|

Corollary 4: If the degree of each vertex is at least k, then −

k|V|  2|E|

Corollary 5: If the degree of each vertex is at most k, then −

k|V|  2|E|