Graph Theory - Coverings

Quiz

Coverings in Graph Theory

A covering graph is a sub-graph which contains either all the vertices or all the edges corresponding to some other graph. A subgraph which contains all the vertices is called a line/edge covering. A sub-graph which contains all the edges is called a vertex covering.

A graph covering ensures that certain elements of a graph (such as edges or vertices) are "covered" by a selected subset of vertices or edges. The most well-known covering problems include the vertex cover, edge cover, and dominating set.

Properties of Covering Graphs

Following are the properties of graph coverings −

Locally Isomorphic: Each neighborhood in the covering graph retains a structural resemblance to its corresponding part in the original graph.
Used in Network Design: Covering graphs help optimize layered network architectures.
Graph Homomorphism: Covering graphs preserve structural properties while expanding the network, making them useful in various applications.

Vertex Cover

A vertex cover of a graph is a set of vertices such that every edge in the graph is incident to at least one vertex in this set. In other words, a vertex cover ensures that all edges are "covered" by selecting a subset of vertices.

Given an undirected graph G = (V, E), a vertex cover is a subset of vertices C ⊆ V such that for every edge (u, v) ∈ E, at least one of u or v belongs to C.

Example

Take a look at the following graph −

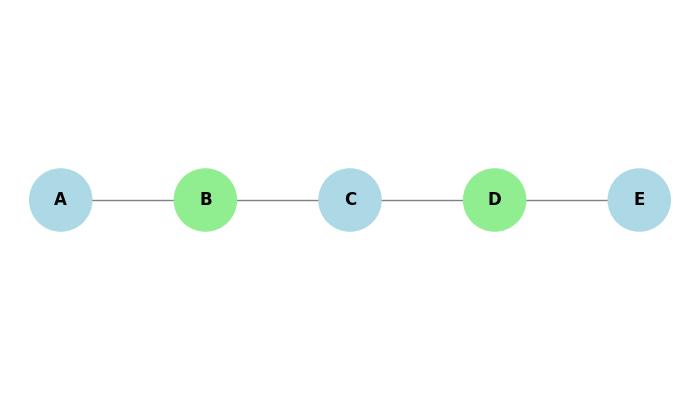
Graph: G = (V, E), where V = {A, B, C, D, E} and E = {(A, B), (B, C), (C, D), (D, E)}.
Vertex Cover: C = {B, D} (since every edge is covered by at least one of these vertices).

Minimal Vertex Cover

A minimal vertex cover is a vertex cover where no vertex can be removed without exposing at least one edge (i.e., leaving an edge uncovered). This means that every vertex in the cover is necessary for maintaining coverage of all edges.

A graph can have multiple minimal vertex covers because different sets of vertices may still ensure full edge coverage.

Being minimal does not mean it has the smallest number of vertices, only that every vertex in the cover is necessary.

Example

In the above graph, each of the following sets covers all edges, and removing any vertex from them would leave some edges uncovered −

{B, D}
{A, C, E}
{A, D}

Minimum Vertex Covering

The minimum vertex cover is the smallest possible vertex cover, i.e., the vertex cover with the fewest number of vertices. It is always minimal, but a minimal vertex cover is not necessarily the minimum vertex cover.

The smallest possible set in the above graph is {B, D} with only 2 vertices.

Edge Cover

An edge cover of a graph is a set of edges such that every vertex in the graph is incident to at least one edge in this set. In other words, an edge cover ensures that all vertices are "covered" by selecting a subset of edges.

Given an undirected graph G = (V, E), an edge cover is a subset of edges C ⊆ E such that for every vertex v ∈ V, there exists an edge (u, v) ∈ C.

Example

Take a look at the following graph −

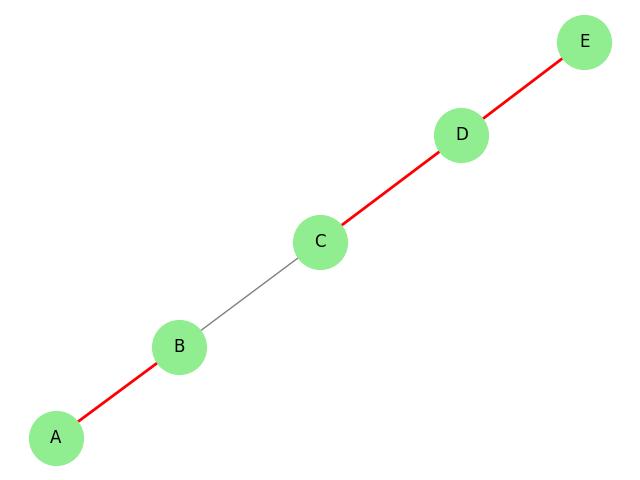
Graph: G = (V, E), where V = {A, B, C, D, E} and E = {(A, B), (B, C), (C, D), (D, E)}.
Edge Cover: C = {(A, B), (C, D), (D, E)} (since every vertex is covered by at least one of these edges).

Minimal Edge Cover

A minimal edge cover is an edge cover where no edge can be removed without exposing at least one vertex (i.e., leaving a vertex uncovered). This means that every edge in the cover is necessary for maintaining coverage of all vertices.

A graph can have multiple minimal edge covers because different sets of edges may still ensure full vertex coverage.

Being minimal does not mean it has the smallest number of edges, only that every edge in the cover is necessary.

Example

In the above graph, each of the following sets covers all vertices, and removing any edge from them would leave some vertices uncovered −

{(A, B), (C, D), (D, E)}
{(A, C), (B, D), (D, E)}
{(A, D), (B, C), (D, E)}

Minimum Edge Covering

The minimum edge cover is the smallest possible edge cover, i.e., the edge cover with the fewest number of edges. It is always minimal, but a minimal edge cover is not necessarily the minimum edge cover.

The smallest possible set in the above graph is {(A, B), (C, D), (D, E)} with only 3 edges.

Line Cover

A line cover of a graph is a set of lines (or edges) such that every edge in the graph is included in at least one of the selected lines. In other words, a line cover ensures that all edges are "covered" by selecting a subset of edges that form paths.

Given an undirected graph G = (V, E), a line cover is a subset of edges C ⊆ E such that for every edge (u, v) ∈ E, there exists a sequence of edges forming a path that covers all edges in the graph.

Example

Take a look at the following graph −

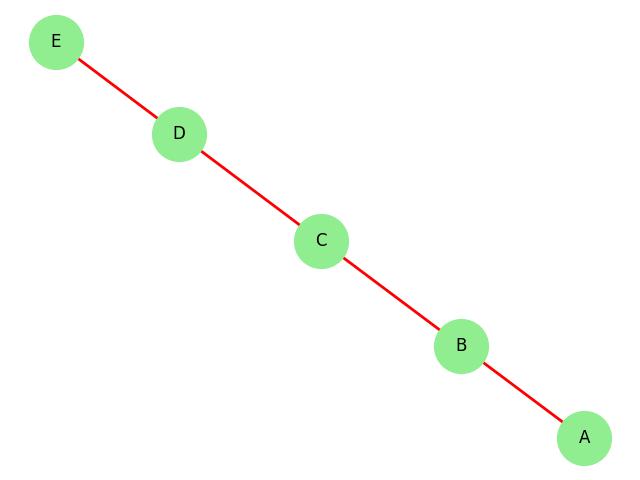
Graph: G = (V, E), where V = {A, B, C, D, E} and E = {(A, B), (B, C), (C, D), (D, E)}.
Line Cover: C = {(A, B), (B, C), (C, D), (D, E)} (since every edge is part of at least one path).

Minimal Line Cover

A minimal line cover is a line cover where no edge can be removed without leaving at least one edge in the graph uncovered. This means that every edge in the cover is necessary for maintaining coverage of all edges.

A graph can have multiple minimal line covers because different sets of edges may still ensure full edge coverage.

Being minimal does not mean it has the smallest number of edges, only that every edge in the cover is necessary.

Example

In the above graph, each of the following sets covers all edges, and removing any edge from them would leave some edges uncovered −

{(A, B), (B, C), (C, D), (D, E)}
{(A, C), (C, D), (D, E)}
{(A, B), (B, D), (D, E)}

Minimum Line Covering

The minimum line cover is the smallest possible line cover, i.e., the cover with the fewest number of edges or paths. It is always minimal, but a minimal line cover is not necessarily the minimum line cover.

The smallest possible set in the above graph is {(A, C), (C, D), (D, E)} with only 3 edges.

Dominating Set

A dominating set of a graph is a subset of vertices such that every vertex in the graph is either in this subset or adjacent to at least one vertex in the subset. In other words, a dominating set ensures that all vertices are "covered" either directly or through their neighbors.

Given an undirected graph G = (V, E), a dominating set D ⊆ V is such that for every vertex v ∈ V, either v ∈ D or there exists a vertex u ∈ D such that (u, v) ∈ E.

Example

Take a look at the following graph −

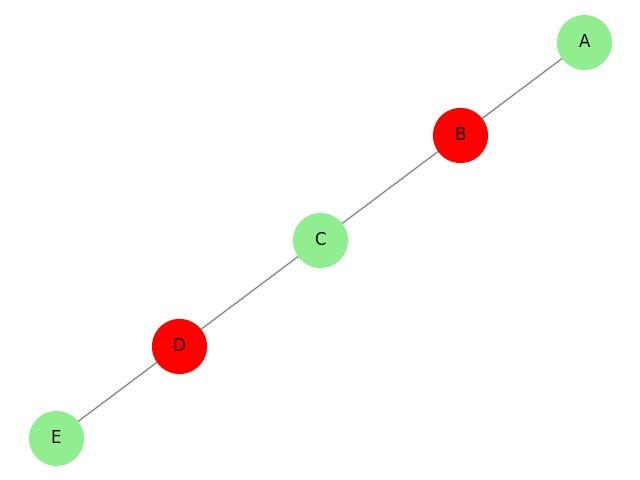
Graph: G = (V, E), where V = {A, B, C, D, E} and E = {(A, B), (B, C), (C, D), (D, E)}.
Dominating Set: D = {B, D} (since every vertex is either in the set or adjacent to one of its vertices).

Minimal Dominating Set

A minimal dominating set is a dominating set where no vertex can be removed without making at least one vertex in the graph undominated. This means that every vertex in the set is necessary for maintaining coverage.

A graph can have multiple minimal dominating sets because different subsets of vertices may still ensure full coverage.

Example

In the above graph, following are the minimal dominating sets −

{B, D}
{A, C, E}
{A, D}

Minimum Dominating Set

The minimum dominating set is the smallest possible dominating set, i.e., the set with the fewest number of vertices. It is always minimal, but a minimal dominating set is not necessarily the minimum dominating set.

The smallest possible set in the above graph is {B, D} with only 2 vertices.

Total Covering

A total covering of a graph is a set of edges such that every vertex in the graph is incident to at least one edge from this set. In other words, a total covering ensures that all vertices are connected through selected edges.

Given an undirected graph G = (V, E), a total covering T ⊆ E is such that for every vertex v ∈ V, there exists at least one edge (u, v) ∈ T.

Example

Take a look at the following graph −

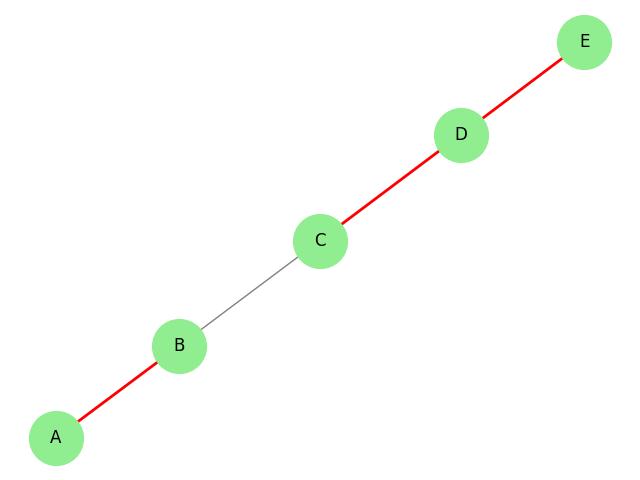
Graph: G = (V, E), where V = {A, B, C, D, E} and E = {(A, B), (B, C), (C, D), (D, E)}.
Total Covering: T = {(A, B), (C, D), (D, E)} (since every vertex is part of at least one of these edges).

Minimal Total Cover

A minimal total cover is a total covering where no edge can be removed without leaving at least one vertex uncovered. This means that every edge in the cover is necessary for maintaining coverage.

A graph can have multiple minimal total covers because different sets of edges may still ensure full coverage.

Example

In the above graph, following are the minimal total covering sets −

{(A, B), (C, D), (D, E)}
{(A, C), (B, D), (D, E)}
{(A, D), (B, C), (D, E)}

Minimum Total Covering

The minimum total cover is the smallest possible total cover, i.e., the set with the fewest number of edges. It is always minimal, but a minimal total cover is not necessarily the minimum total cover.

The smallest possible set in the above graph is {(A, B), (C, D), (D, E)} with only 3 edges.

Print Page