Graph Theory - Graph Minors

Quiz

Graph Minors

Graph minors provides details into the structural properties and relationships between different graphs.

A graph H is said to be a minor of a graph G if H can be obtained from G by performing a series of operations, like −

Edge Deletion: Removing one or more edges from the graph.
Vertex Deletion: Removing one or more vertices from the graph, along with any edges incident to those vertices.
Edge Contraction: Replacing an edge uv with a single vertex that is incident to both u and v, and removing the original edge.

Formally, if H can be derived from G using these operations, then we say that H is a minor of G, denoted as H ≤ G.

For example, if you remove a vertex and its incident edges from a graph, or replace an edge with a simpler structure (contract it), you can generate a minor.

Properties of Graph Minors

Graph minors have several important properties that make them useful for analyzing graphs and understanding their structure −

Minor Closed Property: A graph class is minor-closed if every minor of a graph in that class also belongs to the same class. For example, the class of planar graphs is minor-closed because any minor of a planar graph is also planar.
Minor Theorem: Graph minors are important to a series of theorems in graph theory, including the Robertson-Seymour Theorem, which states that every graph property that is closed under taking minors can be defined by a finite set of forbidden minors.
Minor Invariants: Minors are used to define various graph invariants like tree-width and graph genus, which are important for graph algorithms and understanding graph properties.
Transitivity of Minors: If a graph H is a minor of G, and G is a minor of F, then H is also a minor of F. This transitive property allows reasoning about graph structures across multiple graph relations.

Applications of Graph Minors

Graph minors have various applications across different fields, such as −

Graph Embedding: Minors are used in graph embedding problems, where the objective is to map a graph into a lower-dimensional space while preserving its structure or planarity. The existence of certain minors can guide the embedding process.
Graph Isomorphism: Graph minors are important in graph isomorphism problems, which aim to determine if two graphs are structurally identical. Minor-preserving operations can simplify or reduce the graph, making it easier to compare.
Graph Planarity: Minors are important in defining planar graphs. A graph is planar if and only if it does not contain certain minors, such as the complete graph K₅ or the complete bipartite graph K_3,3.
Treewidth and Graph Decomposition: Graph minors are closely related to treewidth and graph decomposition problems. The treewidth of a graph measures its "tree-likeness," which is useful in designing algorithms for various graph-related problems.
Graph Coloring: Minors play a role in graph coloring problems, where the goal is to assign colors to vertices such that no two adjacent vertices share the same color. Minors can affect the chromatic number and help in the study of coloring properties.

Minor of a Complete Graph (K_n)

A complete graph K_n is a graph where every pair of vertices is connected by an edge. A minor of a complete graph K_n can be obtained by removing some vertices or edges, or contracting some edges.

For example: If we take K₄ (the complete graph on 4 vertices), a minor of K₄ could be a triangle K₃ obtained by deleting one vertex.

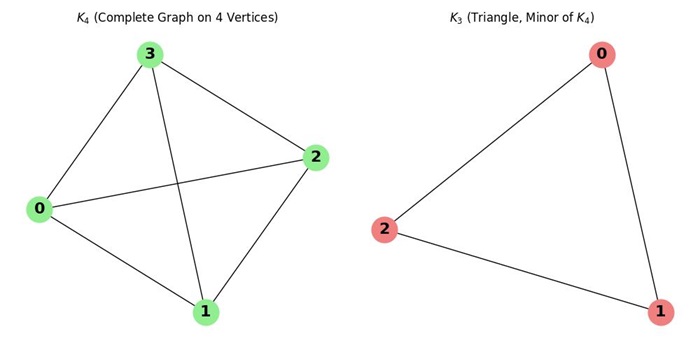
In the above image, we obtain a minor graph K₃ by removing the vertex 3 from the original complete graph K₄.

Minor of a Planar Graph

A planar graph is a graph that can be drawn on a plane without edges crossing. A graph is planar if and only if it does not contain certain minors, such as K₅ (the complete graph on 5 vertices) or K_3,3 (the complete bipartite graph with 3 vertices in each part).

For example: A minor of a planar graph could be K_3,3, which is a non-planar graph, showing that the original graph was non-planar.

In the above image, on the left, the planar graph C₅ is displayed, which is a simple 5-cycle. On the right, the non-planar graph K_3,3 is displayed, which consists of two sets of 3 vertices with edges between all pairs from different sets.

Minor of a Tree

A tree is a graph with no cycles. Any tree is a minor of any connected graph because we can obtain a tree from any connected graph by removing edges and vertices while maintaining the connectivity between the remaining vertices.

For example: A minor of a graph with cycles could be a simple tree by removing edges that form cycles, resulting in a connected acyclic graph.

Here, the second image displays the tree structure obtained by removing one edge from the original graph K₄.

Challenges in Graph Minors

Although graph minors are a powerful concept, determining graph minors can be challenging, particularly for large or complex graphs −

Complexity for Large Graphs: Finding minors in large graphs can be computationally demanding, especially when determining whether a graph contains a specific forbidden minor.
Non-trivial Minor Characterization: For non-trivial graphs with complex structures, identifying the exact minors may require advanced techniques and algorithms.
Graph Reduction: The process of reducing a graph to find minors can sometimes lead to loss of important information, and care must be taken in applying edge contractions or deletions.

Print Page