Graph Theory - Weighted Graphs

---

---

Weighted Graphs

A weighted graph is a graph in which each edge is assigned a numerical value, known as the weight. The weight represents the cost, distance, or any other metric that quantifies the relationship between two vertices.

Weighted graphs are extensively used in applications such as network routing, pathfinding, and resource allocation where the weight of edges influences the decision-making process.

Example

Consider a weighted graph with vertices V = {A, B, C, D} and edges with weights E = {(A - B, 2), (B - C, 3), (C - D, 1), (A - D, 4)}. Here, the weights represent the cost associated with traveling from one vertex to another −

Types of Weighted Graphs

Weighted graphs can be classified based on the nature of the graph and the weights assigned to the edges.

Undirected Weighted Graph

In an undirected weighted graph, the edges have no direction, and the weights represent the cost or distance between the two connected vertices, irrespective of direction.

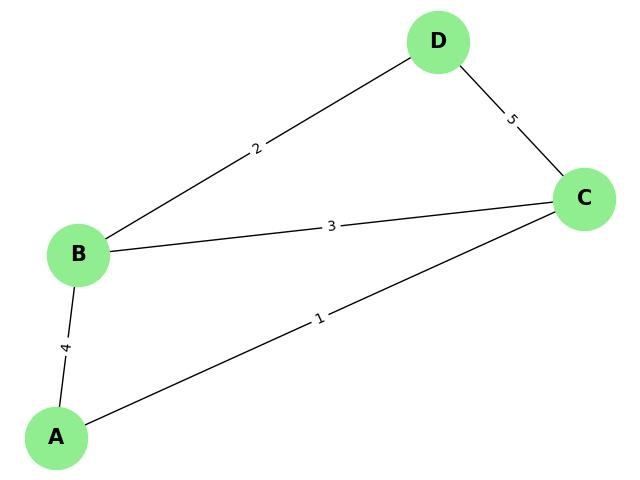
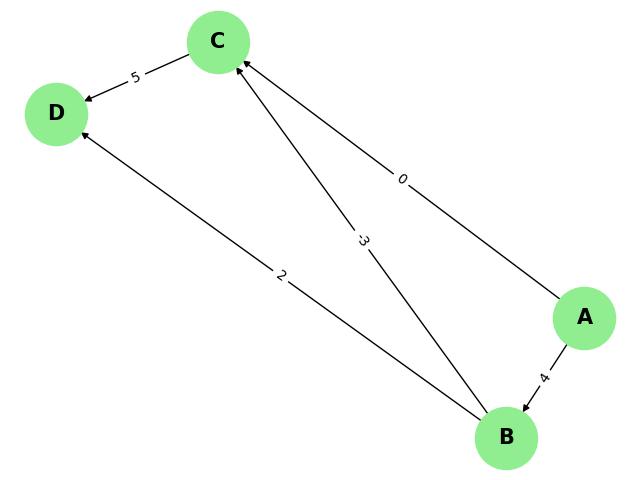
Directed Weighted Graph

In a directed weighted graph, the edges have a specific direction, and the weights represent the cost or distance from the starting vertex to the ending vertex.

Positive and Negative Weights

Weighted graphs can have positive, negative, or zero weights. Positive weights typically represent costs or distances, while negative weights can be used to model benefits or credits. Zero weights indicate no cost or distance between vertices.

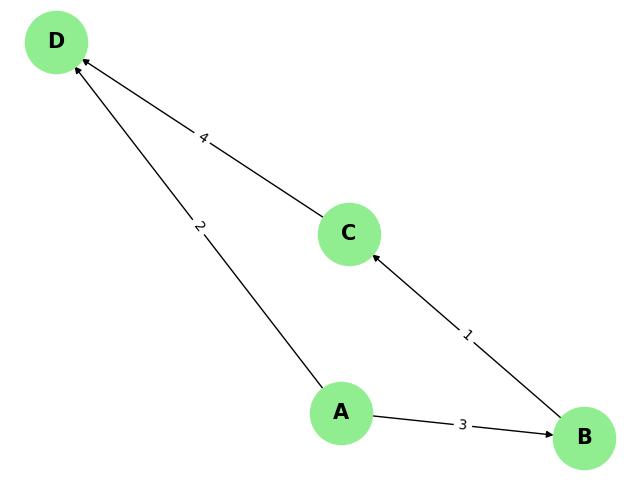
Representation of Weighted Graphs

Weighted graphs can be represented using adjacency matrices, adjacency lists, and edge lists, similar to unweighted graphs, but with additional information about the weights.

Adjacency Matrix Representation

An adjacency matrix for a weighted graph is a square matrix where each entry a[i][j] represents the weight of the edge from vertex i to vertex j. If there is no edge, the entry is typically set to infinity or a designated value indicating no connection.

Example

For a weighted graph with vertices V = {A, B, C, D} and edges with weights E = {(A - B, 3), (B - C, 1), (C - D, 4), (A - D, 2)}, the adjacency matrix would be −

	A	B	C	D
A	0	3		2
B		0	1
C			0	4
D				0

Here, (infinity) indicates no direct edge between the vertices.

Adjacency List Representation

An adjacency list for a weighted graph consists of lists where each vertex points to its adjacent vertices along with the corresponding edge weights.

Example

For the weighted graph with vertices V = {A, B, C, D} and edges with weights E = {(A - B, 3), (B - C, 1), (C - D, 4), (A - D, 2)}, the adjacency list representation would be −

• A: [(B, 3), (D, 2)]
• B: [(C, 1)]
• C: [(D, 4)]
• D: []

Edge List Representation

An edge list for a weighted graph is a list of edges where each edge is represented as a tuple containing the start vertex, end vertex, and the weight.

Example

For the weighted graph with edges E = {(A - B, 3), (B - C, 1), (C - D, 4), (A - D, 2)}, the edge list representation would be −

• (A, B, 3)
• (B, C, 1)
• (C, D, 4)
• (A, D, 2)

Properties of Weighted Graphs

Weighted graphs have several properties that are important for analyzing and solving problems related to costs, distances, and optimizations.

Path Weight

The path weight in a weighted graph is the sum of the weights of the edges that constitute the path. Finding the minimum or maximum path weight is a common problem in graph theory.

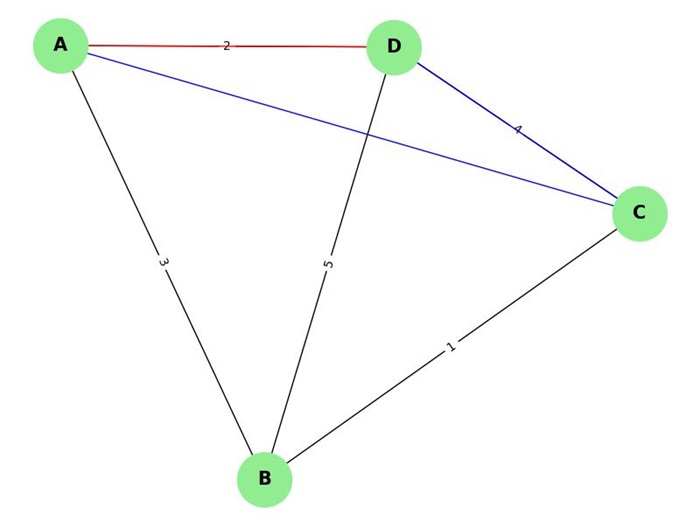
In the above image −

Path Weight: {('A', 'B', 'C'): 4, ('A', 'B', 'D'): 8, ('A', 'D'): 2, ('A', 'C', 'D'): inf}
Minimum Path: ('A', 'D') | Weight: 2
Maximum Path: ('A', 'C', 'D') | Weight: inf

Minimum Spanning Tree (MST)

A Minimum Spanning Tree (MST) is a subset of the edges of a connected, weighted, undirected graph that connects all the vertices together, without any cycles, and with the minimum possible total edge weight. In other words, it is a way of connecting all the nodes in a graph with the least possible total weight of the edges.

In the above image −

MST Edges: [('A', 'D', {'weight': 2}), ('A', 'B', {'weight': 3}), ('B', 'C', {'weight': 1})]

Shortest Path

The shortest path in a graph is the path between two vertices that has the smallest possible total edge weight or distance. The path is defined by a sequence of edges connecting the two vertices, and the total weight is the sum of the weights of the edges along the path.

In some cases, the edges may have a uniform weight (e.g., each edge has a weight of 1), and in others, the weights may vary.

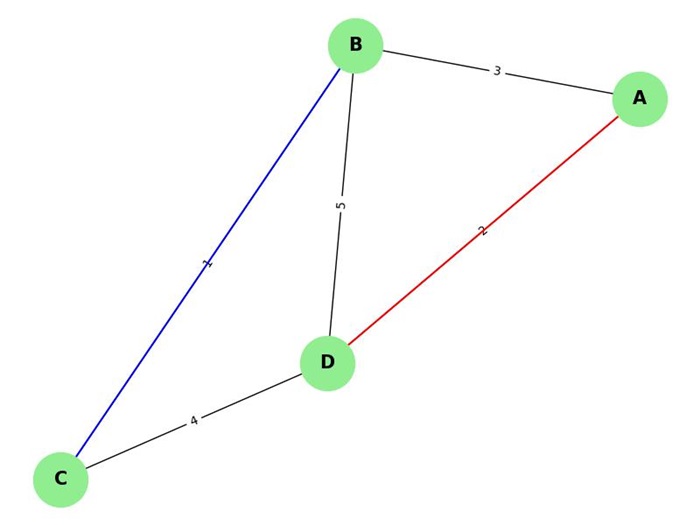
In the above image −

Shortest Path A  D: ['A', 'D'] | Weight: 2
Shortest Path B  C: ['B', 'C'] | Weight: 1

Algorithms for Weighted Graphs

Several algorithms are designed to handle the complexities of edge weights in graphs, including finding the shortest paths, minimum spanning trees, and network flows.

Dijkstra's Algorithm

Dijkstra's Algorithm is used to find the shortest path from a source vertex to all other vertices in a graph with non-negative edge weights. It uses a priority queue to explore the shortest known paths first.

Example

Given a graph with vertices V = {A, B, C, D} and weighted edges E = {(A - B, 3), (B - C, 1), (C - D, 4), (A - D, 2)}, Dijkstra's algorithm will find the shortest paths from the source vertex A to all other vertices.

Bellman-Ford Algorithm

Bellman-Ford Algorithm is used to find the shortest path from a source vertex to all other vertices in a graph, even if the graph contains edges with negative weights. It iteratively relaxes the edges to find the shortest path.

Example

Given a graph with vertices V = {A, B, C, D} and weighted edges E = {(A - B, 3), (B - C, 1), (C - D, 4), (A - D, 2), (D - B, -5)}, the Bellman-Ford algorithm will find the shortest paths from the source vertex A to all other vertices, even considering the negative weight edge (D - B, -5).

Floyd-Warshall Algorithm

Floyd-Warshall Algorithm is used to find the shortest paths between all pairs of vertices in a weighted graph. It works with both positive and negative edge weights and uses a dynamic programming approach.

Example

Given a graph with vertices V = {A, B, C, D} and weighted edges E = {(A - B, 3), (B - C, 1), (C - D, 4), (A - D, 2), (D - B, -5)}, the Floyd-Warshall algorithm will compute the shortest paths between all pairs of vertices.

Kruskal's Algorithm

Kruskal's Algorithm is used to find the Minimum Spanning Tree (MST) of a weighted graph. It sorts all edges by weight and adds them to the MST one by one, ensuring no cycles are formed.

Example

Given a graph with vertices V = {A, B, C, D} and weighted edges E = {(A - B, 3), (B - C, 1), (C - D, 4), (A - D, 2)}, Kruskal's algorithm will find the MST by adding edges in the order of their weights until all vertices are connected without forming cycles.

Prim's Algorithm

Prim's Algorithm is another algorithm for finding the Minimum Spanning Tree (MST) of a weighted graph. It starts with a single vertex and grows the MST by adding the smallest weight edge that connects a vertex in the MST to a vertex outside it.

Example

Given a graph with vertices V = {A, B, C, D} and weighted edges E = {(A - B, 3), (B - C, 1), (C - D, 4), (A - D, 2)}, Prim's algorithm will start from a vertex, say A, and iteratively add the smallest weight edge connecting a new vertex to the MST until all vertices are included.