Graph Theory - Types of Graphs

Quiz

Types Of Graphs

In graph theory, graphs are used to represent relationships between objects. A graph consists of vertices (nodes) and edges (connections between nodes).

In graph theory, there are various types of graphs, each with unique properties and applications. This tutorial covers the most common types of graphs with explanations and examples.

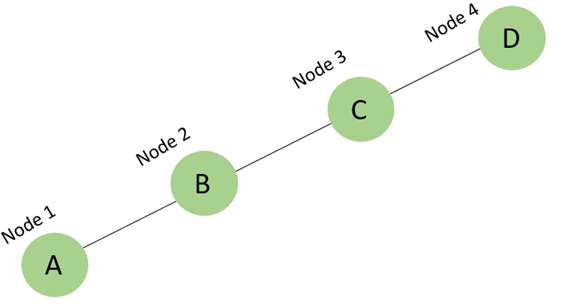
Simple Graph

A simple graph is a type of graph where there are no loops (edges that connect a vertex to itself) and no multiple edges between any pair of vertices. In other words, each pair of vertices is connected by at most one edge, and each edge connects two distinct vertices.

Example: Simple Graph

The following image displays a simple graph with vertices connected by single edges −

Multigraph

A multigraph is a type of graph in which multiple edges are allowed between the same pair of vertices.

Unlike a simple graph, where there is at most one edge between any two vertices, a multigraph can have more than one edge connecting the same pair of vertices. These multiple edges are often called "parallel edges."

Example: Multigraph

The image represents a multigraph where nodes (A, B, C, D) are connected by multiple types of relationships such as friend, coworker, family, and neighbor. Each edge is labeled with its relationship type, and multiple edges between the same nodes are curved to distinguish them visually −

The relationships are mentioned as follows −

'A', 'B', relationship='friend'
'A', 'B', relationship='coworker'
'A', 'C', relationship='family'
'B', 'D', relationship='neighbor'
'A', 'D', relationship='friend'
'A', 'D', relationship='coworker'

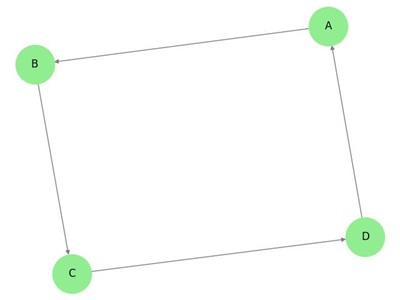
Directed Graph (Digraph)

A directed graph, or digraph, is a type of graph in which the edges have a direction. In other words, each edge in a directed graph points from one vertex to another, indicating a one-way relationship.

The direction of the edge is often represented by an arrow, showing the flow from the starting vertex (source) to the ending vertex (destination).

Example: Directed Graph

The following image demonstrates a directed graph with edges having specific directions −

Undirected Graph

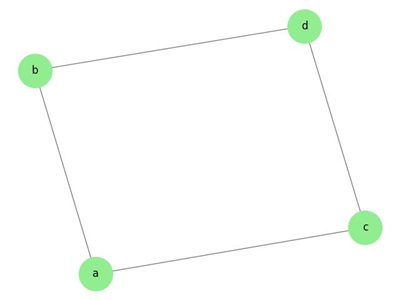
An undirected graph is a type of graph in which the edges do not have a direction. In other words, the relationship between two vertices is mutual, meaning that if there is an edge between vertex A and vertex B, you can travel in both directions between them.

Example: Undirected Graph

This image displays an undirected graph with edges having no directions −

Weighted Graph

A weighted graph is a type of graph where each edge is assigned a weight, usually representing some form of cost, distance, or value. These weights can be used to represent a variety of metrics, such as travel time, distance between locations, or bandwidth in a network.

Example: Weighted Graph

The following image illustrates a weighted graph with edges labeled with weights −

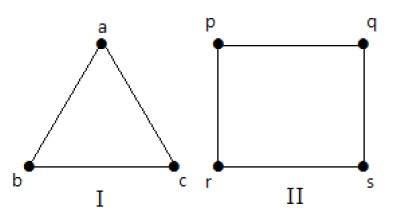
Complete Graph

A complete graph is a type of graph in which every pair of distinct vertices is connected by a unique edge. In other words, every vertex is directly connected to every other vertex in the graph. A complete graph with n vertices is denoted by K_n.

Example: Complete Graph

The following image shows a complete graph with five vertices −

Bipartite Graph

A bipartite graph is a type of graph in which the vertices can be divided into two distinct sets such that no two vertices within the same set are adjacent.

In other words, every edge connects a vertex from one set to a vertex from the other set, and there are no edges connecting vertices within the same set.

Example: Bipartite Graph

The following image demonstrates a bipartite graph with two sets of vertices −

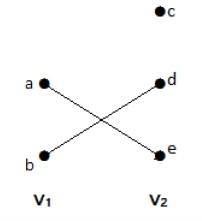
Complete Bipartite Graph

A complete bipartite graph is a special type of bipartite graph where every vertex in the first set is connected to every vertex in the second set by a unique edge.

In other words, there are no edges within each set, but every possible edge between the two sets is present, making it "complete" between the two sets.

Example: Complete Bipartite Graph

Following image displays complete bipartite graph −

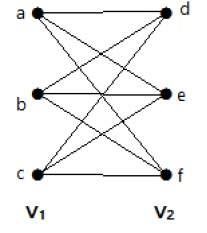
Planar Graph

A planar graph is a type of graph that can be drawn on a flat surface without any of its edges crossing each other. This means you can place the vertices (points) and edges (lines connecting the points) in such a way that no two edges overlap, except at their endpoints.

Example: Planar Graph

The following image shows a planar graph drawn without any crossing edges −

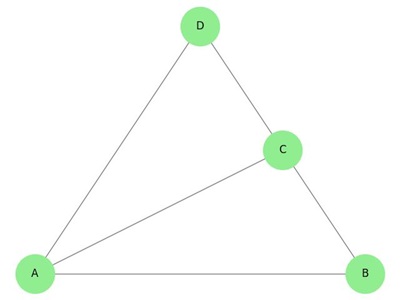
Non-Planar Graph

A non-planar graph is a type of graph that cannot be drawn on a flat surface without some of its edges crossing each other. No matter how you try to arrange the vertices and edges, there will always be at least one pair of edges that intersect.

Example: Non-Planar Graph

Following image displays a non-planar graph −

Tree

A tree is a type of graph that has the following characteristics −

Connected: There is a path between any two vertices in the graph. This means all the vertices are linked together, directly or indirectly.
Acyclic: It does not contain any cycles. A cycle is a path that starts and ends at the same vertex without repeating any edges or vertices (except the starting/ending vertex).

In simpler terms, a tree graph looks like a family tree or an organizational chart. It starts from a single point called the "root" and branches out, with no loops or circles in the structure. Each branch splits into more branches or ends at a "leaf" (a vertex with no further branches).

A tree with n vertices has n-1 edges.

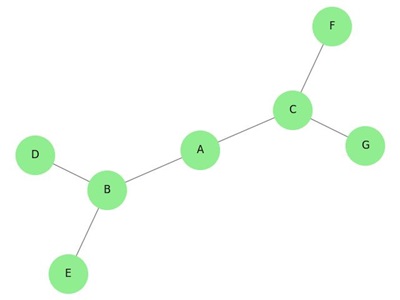
Example: Tree

The following image demonstrates a tree structure −

Forest

A forest is a collection of one or more disjoint trees. In other words, it's a graph that consists of multiple trees, where each tree is a separate, connected, acyclic subgraph.

Here are the key points about a forest −

Disjoint Trees: Each tree in a forest is separate from the others; there are no edges connecting vertices in different trees.
Acyclic: Like trees, each tree in a forest does not contain any cycles.
Collection of Trees: A forest can have one or more trees.

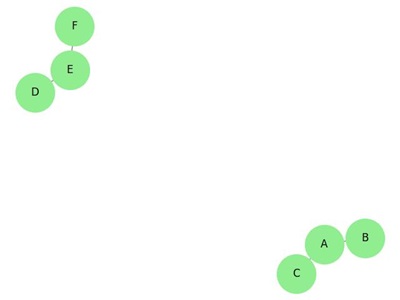
Example: Forest

The following image illustrates a forest consisting of two separate trees −

Cycle Graph

A cycle graph is a type of graph that consists of a single cycle. In a cycle graph, each vertex is connected to exactly two other vertices, forming a closed loop. This means you can start at any vertex, follow the edges, and return to the starting vertex without retracing any edge or visiting any vertex more than once (except the starting vertex).

Here are the key points about a cycle graph −

Single Cycle: There is one continuous loop.
Equal Degree: Every vertex has a degree of 2 (each vertex is connected to exactly two other vertices).
Connected and Acyclic: It is a connected graph without any other cycles except the one that defines it.

Example: Cycle Graph

The following image shows a cycle graph with five vertices −

Cyclic Graph

A cyclic graph is a type of graph that contains at least one cycle. In other words, it has a path that starts from a vertex and returns to the same vertex without retracing any edges, forming a closed loop. Unlike acyclic graphs (such as trees), cyclic graphs have one or more such loops.

Here are the key points about a cyclic graph −

Contains Cycles: The defining feature is the presence of one or more cycles.
Connected or Disconnected: A cyclic graph can be either connected (all vertices are reachable from any other vertex) or disconnected (composed of multiple connected components).
Versatile Structure: Cyclic graphs can have various shapes and sizes, as long as they include at least one cycle.

Example: Cyclic Graph

The following image displays a cyclic graph −

Acyclic Graph

An acyclic graph is a type of graph that does not contain any cycles. In other words, there are no paths that start and end at the same vertex without retracing any edges. This means that once you travel along an edge in an acyclic graph, you cannot return to the starting point by following a different set of edges.

Here are the key points about an acyclic graph −

No Cycles: The defining feature is the absence of cycles in the graph.
Connected or Disconnected: An acyclic graph can be either connected (all vertices are reachable from any other vertex) or disconnected (composed of multiple separate components).
Tree-like Structure: Acyclic graphs often resemble tree structures, where each vertex is connected in a non-circular way.

Example: Acyclic Graph

The following image shows an acyclic graph −

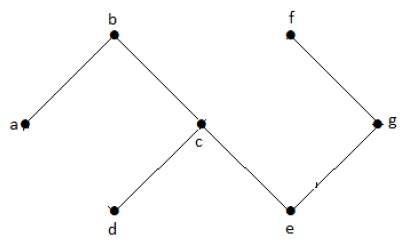
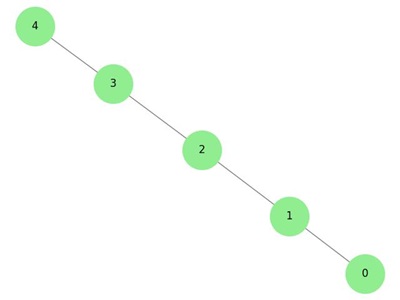
Path Graph

A path graph is a graph in which vertices are arranged in a linear sequence, with each vertex connected to exactly two other vertices (except for the endpoints, which are connected to only one other vertex).

Example: Path Graph

The following image illustrates a path graph with five vertices −

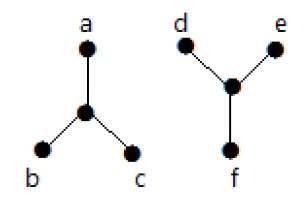
Star Graph

A star graph is a graph in which one central vertex is connected to all other vertices, forming a star-like structure. There are no other edges in the graph.

Example: Star Graph

The following image demonstrates a star graph with five outer vertices −

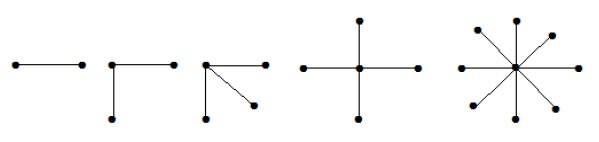
Wheel Graph

A wheel graph is a graph formed by connecting a single central vertex to all vertices of a cycle graph. The central vertex is connected to every other vertex in the cycle.

Example: Wheel Graph

The following image shows a wheel graph with six vertices (including the central vertex) −

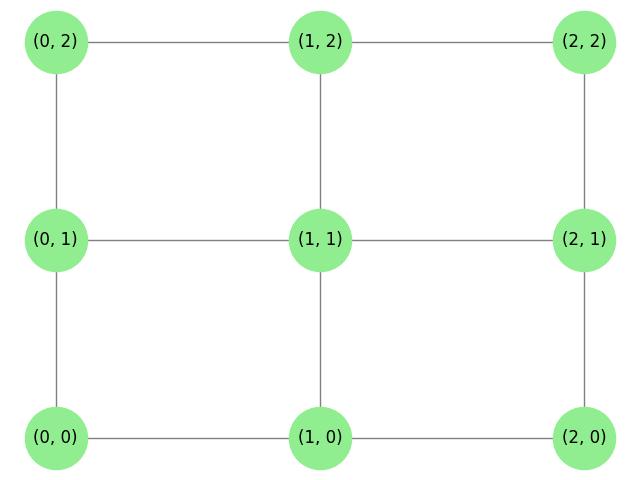
Grid Graph

A grid graph is a type of graph where the vertices are arranged in a grid-like pattern, with edges connecting adjacent vertices either horizontally or vertically (or both). It can be thought of as a graph where the vertices represent points on a 2D grid and the edges represent connections between neighboring points.

Example: Grid Graph

The following image illustrates a 3x3 grid graph −

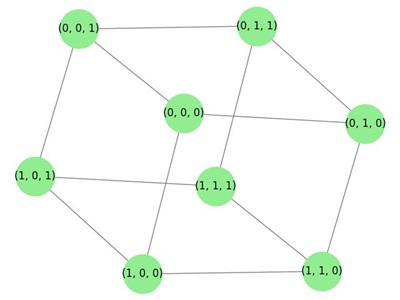
Hypercube Graph

A hypercube graph is a type of graph that represents the vertices and edges of an n-dimensional hypercube.

It is a generalization of the cube in higher dimensions. In a hypercube graph, each vertex corresponds to a binary string of length n, and two vertices are connected by an edge if and only if their binary strings differ by exactly one bit.

Example: Hypercube Graph

The following image demonstrates a 3-dimensional hypercube graph (also known as a cube graph) −

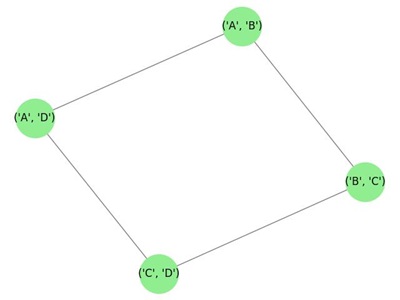
Line Graph

A line graph is a type of graph that represents the adjacency relationships between edges of another graph. In a line graph, the vertices represent the edges of the original graph, and two vertices are connected if the corresponding edges in the original graph share a common vertex.

Example: Line Graph

The following image shows a line graph derived from a simple graph −

Null Graph

A null graph is a type of graph that has no edges. It consists only of vertices, but there are no connections (edges) between them. In other words, the graph is completely disconnected.

Example: Null Graph

The following image shows a null graph −

Trivial Graph

A trivial graph is a type of graph that contains only one vertex and no edges. It is the simplest possible graph, where the single vertex is not connected to anything.

Example: Trivial Graph

The following image displays a trivial graph −

Connected Graph

A connected graph is a type of graph in which there is a path between every pair of vertices. In other words, for any two vertices in the graph, there is a way to travel from one vertex to the other by following the edges of the graph.

Example: Connected Graph

The following image shows a connected graph −

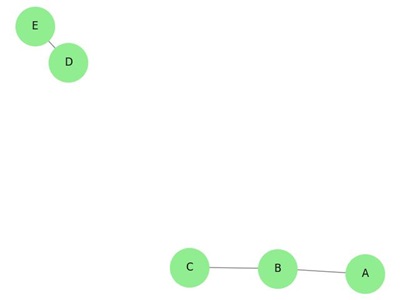
Disconnected Graph

A disconnected graph is a type of graph in which there are at least two vertices that do not have a path connecting them. In other words, the graph is not connected, and some vertices or groups of vertices are isolated from others.

Example: Disconnected Graph

The following image displays a connected graph −

Regular Graph

A regular graph is a type of graph in which each vertex has the same degree, meaning that every vertex is connected to the same number of edges. In other words, all vertices in a regular graph have an equal number of neighbors.

Example: Regular Graph

The following image shows a regular graph −

Sparse Graph

A sparse graph is a type of graph in which the number of edges is much smaller compared to the number of vertices. In other words, most of the possible edges in the graph are missing, making the graph relatively "empty" in terms of edge connections.

Example: Sparse Graph

The following image shows a sparse graph −

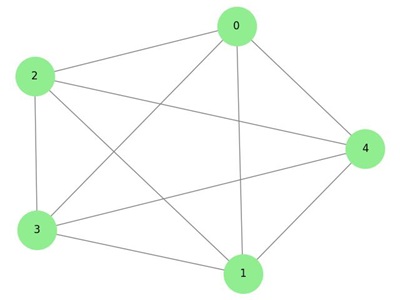
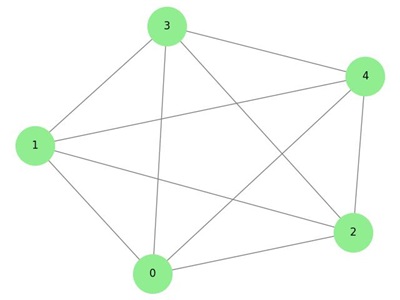
Dense Graph

A dense graph is a type of graph in which the number of edges is close to the maximum possible number of edges for a given number of vertices. In other words, most of the possible edges are present, making the graph highly connected.

Example: Dense Graph

The following image displays a dense graph −

Labeled Graph

A labeled graph is a type of graph in which each vertex and/or edge is assigned a unique label or identifier. These labels are used to distinguish between different vertices or edges, providing additional information or making it easier to reference specific parts of the graph.

Example: Labeled Graph

The following image displays a labeled graph −

Print Page