Graph Theory - Orthogonal Graph Drawing

Orthogonal Graph Drawing

Orthogonal Graph Drawing is a way of drawing graphs where the edges are made up of only straight lines that are either horizontal or vertical.

This technique is helpful for drawing graphs where it is important to keep edges the same length. It uses straight lines with 90-degree angles to make the connections simple and easy to follow. This approach keeps the graph neat and avoids overly complicated edge shapes.

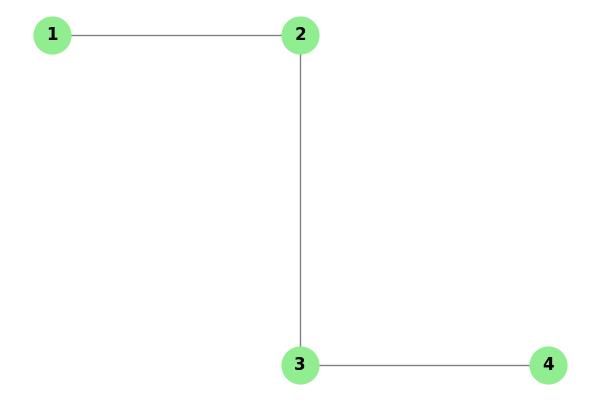
The image above demonstrates an orthogonal graph drawing, where each edge is represented as either a horizontal or vertical line, forming right angles at the vertices.

Principles of Orthogonal Graph Drawing

Orthogonal graph drawing follows several important principles to make graphs more structured and easy to understand −

• Orthogonal Edges: All edges are drawn using horizontal and vertical lines. This simplifies the geometry of the graph and makes the layout more structured.
• Minimizing Edge Crossings: Orthogonal graph drawing tries to avoid edge crossings, which can improve the clarity of the graph.
• Layered Placement: Nodes are often placed in horizontal or vertical layers, with edges connecting nodes through a series of orthogonal line segments.
• Uniformity: The edges are kept similar in length to avoid any lines being too long or too short, making the graph look balanced.

Orthogonal Graph Drawing Algorithms

Orthogonal graph drawing uses different methods to place nodes and edges neatly, making sure edges follow straight horizontal and vertical lines while avoiding edge crossings. Following are some popular algorithms −

• Fry's Algorithm: It finds a way to draw a graph without overlapping edges, using only straight, right-angle lines.
• Layered Orthogonal Drawing Algorithm: Nodes are arranged in rows or columns (layers), and edges are drawn as straight lines connecting these layers, keeping the graph organized.
• Grid-based Orthogonal Drawing: Nodes are placed on a grid, like points on graph paper, and edges follow the grid lines to stay perfectly horizontal or vertical.
• Multi-level Orthogonal Drawing: This method uses multiple steps to refine the graph, reducing edge overlaps and making it look cleaner and more balanced.

Fry's Algorithm

Fry's Algorithm is a basic method used in orthogonal graph drawing to make sure a graph can be drawn with straight edges at right angles. Here is how it works −

• Step 1 - Planar Graph Embedding: The first step is to place the graph on a flat surface so that no edges cross each other. This makes sure the graph is laid out clearly without overlapping lines.
• Step 2 - Orthogonalization: Then, the edges are adjusted so that they form straight lines with 90-degree turns at each corner, making the graph look neat.
• Step 3 - Edge Routing: The edges are drawn along horizontal and vertical lines, making sure everything stays aligned and the graph remains clean and easy to follow.

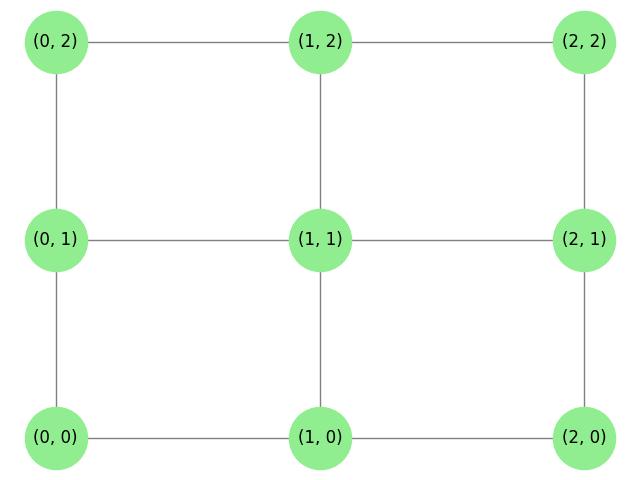
The above image shows the result of applying Fry's Algorithm to a planar graph, demonstrating the transformation of the graph into an orthogonal layout with minimal edge crossings.

Challenges in Orthogonal Graph Drawing

Orthogonal graph drawing comes with several challenges, especially when dealing with large or dense graphs −

• Edge Crossings: Even though edges are drawn at right angles, in dense graphs, some edges may still cross over each other, making the graph harder to read.
• Node Placement: Finding the right position for each node while making sure the edges are orthogonal (straight and at right angles) can be difficult and time-consuming.
• Complexity of Large Graphs: As the graph grows larger, it becomes harder to manage the placement of nodes and edges without the graph looking cluttered.
• Uniform Edge Lengths: Ensuring that all edges have the same length while maintaining the orthogonal layout can be challenging in some situations.

Optimizations for Orthogonal Graph Drawing

To address the challenges of orthogonal graph drawing, we can use several optimization techniques −

• Crossing Minimization: Algorithms like Fry's Algorithm are used to minimize edge crossings, ensuring that the final drawing remains clear.
• Grid-based Layouts: Using a grid-based layout can help ensure that edges are drawn orthogonally and that nodes are evenly spaced.
• Edge Length Normalization: Algorithms can normalize (uniform) edge lengths, ensuring that all edges are of similar length for a more balanced layout.
• Layered Orthogonal Drawing: This technique places nodes into layers and routes edges between them in a way that keeps the edges at right angles and minimizes crossings.