Graph Theory - Graph Representation

Quiz

Graph Representation

Graph representation refers to the way a graph is stored and organized in a computer's memory. Since graphs consist of vertices (nodes) and edges (connections between nodes), representing them is important for performing graph-related operations like searching, traversing, or finding the shortest path.

There are three major types of graph representations, each with its own advantages and use cases −

Adjacency Matrix: A 2D array used to represent the graph where each element indicates whether an edge exists between two vertices.
Adjacency List: A collection of lists or arrays where each list contains the neighbors of a particular vertex (i.e., the vertices it is connected to).
Edge List: A collection of all edges in the graph, where each edge is represented by a pair or tuple of vertices.

The choice of graph representation depends on factors such as the size of the graph, the density of edges, and the types of operations that need to be performed.

Adjacency Matrix

An adjacency matrix is a 2D array that is used to represent a graph, where the rows and columns represent the vertices. The element at the intersection of a row and column represents whether there is an edge between the two corresponding vertices.

For a graph with n vertices, the adjacency matrix is a square matrix of size n x n. If there is an edge between vertex i and vertex j, the element at matrix[i][j] is 1; otherwise, it is 0.

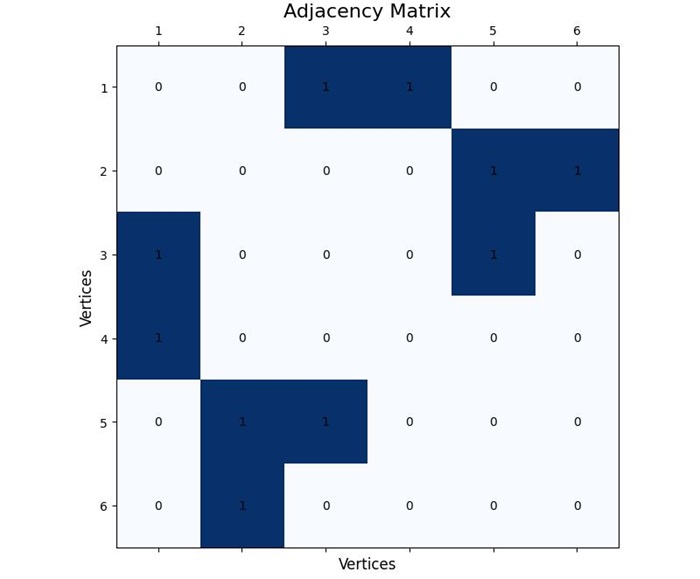
Adjacency Matrix:
[[0 0 1 1 0 0]
 [0 0 0 0 1 1]
 [1 0 0 0 1 0]
 [1 0 0 0 0 0]
 [0 1 1 0 0 0]
 [0 1 0 0 0 0]]

Properties of Adjacency Matrix

Following are the basic properties of adjacency matrix −

Space Complexity: O(n), where n is the number of vertices in the graph.
Edge Lookup: Checking for an edge between two vertices is O(1), as it is a direct lookup in the matrix.
Memory Usage: It is memory inefficient for sparse graphs, as it always uses space for all possible edges, even if many are missing.

For instance, for an undirected graph with vertices V = {A, B, C} and edges {A-B, A-C}, the adjacency matrix would be −

Adjacency List

An adjacency list is a collection of lists or arrays where each list stores the neighbors of a specific vertex. Each vertex has its own list, and the list contains the vertices that it is connected to via edges.

This representation is more space-efficient for sparse graphs, as it only stores the edges that actually exist in the graph.

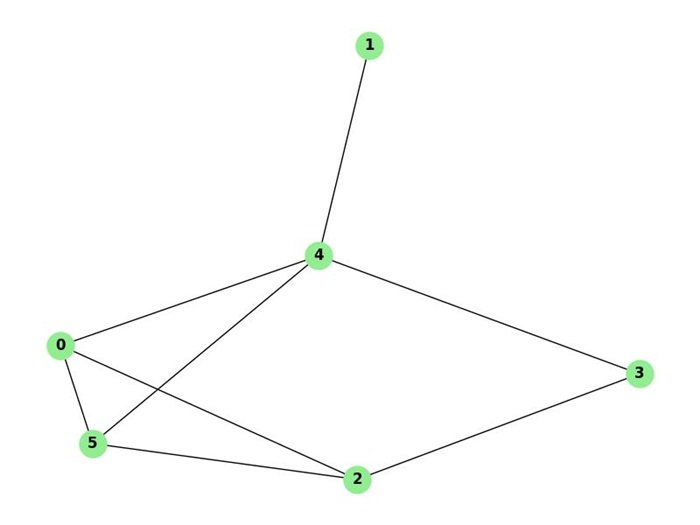
The adjacency lists for this graph is as follows −

Adjacency List Representation:
Node 0: [2, 4, 5]
Node 1: [4]
Node 2: [0, 3, 5]
Node 3: [2, 4]
Node 4: [0, 1, 3, 5]
Node 5: [0, 2, 4]

Properties of Adjacency List

Following are the basic properties of adjacency list −

Space Complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Edge Lookup: Finding the neighbors of a vertex is O(degree of vertex), as we need to scan through the list.
Memory Usage: More memory efficient for sparse graphs compared to the adjacency matrix.

For instance, for the same graph V = {A, B, C} with edges {A-B, A-C}, the adjacency list would be −

A -> B, C
B -> A
C -> A

Edge List

An edge list is simply a list or collection of all the edges in a graph. Each edge is represented as a pair (or tuple) of vertices that it connects. This representation is useful for algorithms that primarily focus on the edges rather than the structure of the graph.

The edge list is typically used in problems that involve a list of edges without the need for vertex-to-vertex lookups.

Properties of Edge List

Following are the basic properties of edge list −

Space Complexity: O(E), where E is the number of edges in the graph.
Edge Lookup: To check if an edge exists, you would need to scan the list, making it an O(E) operation.
Memory Usage: Efficient in terms of space when the number of edges is small or the graph is sparse.

For instance, for the same graph V = {A, B, C} with edges {A-B, A-C}, the edge list would be −

(A, B), (A, C)

Weighted Graph

Graphs can also be weighted, meaning that each edge carries a weight or value, which can represent distance, cost, or any other metric. Weighted graphs can be represented using any of the previous methods with an additional step to store the edge weights.

Adjacency Matrix for Weighted Graphs

In a weighted graph, the adjacency matrix stores the weights instead of just 1 or 0. The element matrix[i][j] will store the weight of the edge between vertices i and j, or infinity () if no edge exists.

For instance, for a weighted undirected graph with vertices V = {A, B, C} and edges {A-B: 5, A-C: 3}, the weighted adjacency matrix would be −

Adjacency List for Weighted Graphs

In a weighted adjacency list, each list entry not only contains the neighboring vertices but also the weight of the edge. Each vertex has a list of pairs, where each pair consists of a neighboring vertex and the weight of the edge.

For the same weighted graph, the adjacency list would be −

A -> (B, 5), (C, 3)
B -> (A, 5)
C -> (A, 3)

Edge List for Weighted Graphs

In the edge list representation for weighted graphs, each edge is represented as a tuple containing two vertices and the weight of the edge between them.

For the same weighted graph, the edge list would be −

(A, B, 5), (A, C, 3)

Graph Representation for Directed Graphs

In directed graphs, the edges have a direction. This means that an edge from vertex A to vertex B is not necessarily the same as an edge from vertex B to vertex A. Directed graphs can be represented using any of the methods discussed above, with attention to the direction of the edges.

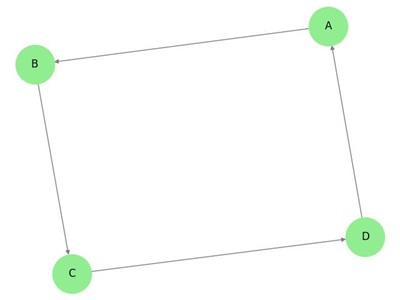
Adjacency Matrix for Directed Graphs

In the adjacency matrix for directed graphs, the element matrix[i][j] is 1 if there is a directed edge from vertex i to vertex j, and 0 if there is no such edge.

For instance, for a directed graph with vertices V = {A, B, C} and edges {A->B, A->C}, the adjacency matrix would be −

Adjacency List for Directed Graphs

In the adjacency list for directed graphs, each vertex's list contains only its outgoing edges, i.e., vertices that it has a directed edge to.

For the same directed graph, the adjacency list would be −

A -> B, C
B -> 
C ->

Edge List for Directed Graphs

In the edge list for directed graphs, each edge is a directed pair of vertices. The edge (A, B) means there is an edge from vertex A to vertex B.

For the same directed graph, the edge list would be −

(A, B), (A, C)

Comparing Graph Representations

Each graph representation has its own advantages and drawbacks. The following table summarizes the strengths and weaknesses of each representation −

Representation	Space Complexity	Edge Lookup	Edge Insertion
Adjacency Matrix	O(n)	O(1)	O(1)
Adjacency List	O(V + E)	O(degree of vertex)	O(1)
Edge List	O(E)	O(E)	O(1)

Print Page