Graph Theory - Four Color Theorem

---

---

The Four Color Theorem

The Four Color Theorem states that four colors are sufficient to color any map in such a way that no two adjacent regions share the same color.

This means that if a map can be represented as a graph where regions are vertices and shared borders between regions are edges, it is always possible to color the map using no more than four colors without having adjacent regions share the same color.

This theorem applies to planar graphs, which are graphs that can be drawn on a flat surface without any edges crossing each other.

Statement of the Four Color Theorem

The statement of the Four Color Theorem is as follows −

• Theorem: Any planar graph can be colored with no more than four colors such that no two adjacent vertices share the same color.

Four Color Theorem Graph Representation

In graph theory terms, the Four Color Theorem can be represented as follows −

• Vertices: Represent the regions or areas that need to be colored.
• Edges: Represent the adjacency (shared borders) between regions. If two regions share a common boundary, there is an edge between their corresponding vertices.

The challenge, then, is to assign a color to each vertex such that no two adjacent vertices (representing adjacent regions) share the same color. The theorem guarantees that this can always be done with at most four colors.

History of the Four Color Theorem

The Four Color Theorem was first suggested in 1852 by Francis Guthrie, a British mathematician. It remained an unsolved problem for over a century, attracting attention from many mathematicians.

Despite several attempts, a general proof was hard to find until 1976, when Kenneth Appel and Wolfgang Haken used a computer to help prove the theorem.

The proof involved checking a large number of individual cases (1,936 different configurations), which would have been impossible to do by hand. This computer-assisted proof was groundbreaking, as it was the first time a major mathematical theorem had been proven using a computer. Although the proof was controversial at first, it has since been widely accepted.

Understanding Planar Graphs

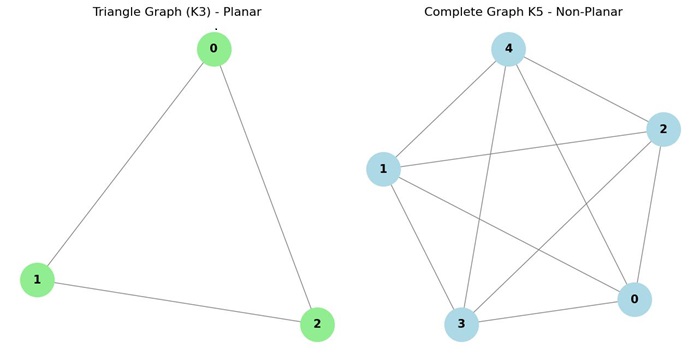
In order to understand the Four Color Theorem, it's important to first understand the concept of planar graphs. A planar graph is a graph that can be drawn on a plane (a flat surface) such that no edges intersect, except at their endpoints. This means that the graph can be embedded in the plane without any edge crossings.

For example, a simple graph like a triangle is planar because it can be drawn on a piece of paper without any edges crossing. On the other hand, the complete graph K5 (which consists of five vertices with edges connecting every pair of vertices) is not planar, as it cannot be drawn without edge crossings.

Proof of the Four Color Theorem

The Four Color Theorem was finally proven in 1976 by Kenneth Appel and Wolfgang Haken, after many years of unsuccessful attempts by mathematicians.

Their proof was groundbreaking because it involved a computer-assisted check of many possible cases, something that had not been done in mathematical proofs before. Here is an overview of how the proof works −

• Reduction to Simpler Cases: Appel and Haken's proof involved reducing the problem to a set of simpler cases. They identified a set of unavoidable configurations that must appear in any graph that needs more than four colors, and showed that these configurations could all be reduced to smaller graphs that could be easily solved.
• Use of Computer Assistance: The proof required the assistance of a computer to check the existence of these configurations. This part of the proof involved analyzing a vast number of possible graphs (around 1,936) to ensure that none of them required more than four colors. The computer used algorithms to check these graphs systematically.
• Verification of Configuration Cases: Each of the identified configurations was verified manually by Appel and Haken, ensuring that no graph violated the four-color rule.

While the proof was groundbreaking, it also sparked controversy and debate due to its reliance on computers. Some mathematicians argued that the use of computers for such a proof didn't constitute a true mathematical proof, as humans could not independently verify all the cases.

However, the proof remains accepted as valid in the mathematical community, even though it's considered less "elegant" than traditional, purely analytical proofs.

Applications of the Four Color Theorem

The Four Color Theorem has several practical applications, particularly in areas that involve the allocation of resources or the prevention of conflicts. Some of the important applications are −

• Map Coloring: The most direct application of the Four Color Theorem is in map coloring, where regions of a map are represented as vertices in a graph. The theorem ensures that no more than four colors are required to color the map, making it easier to design maps that are visually distinct and easy to read.
• Scheduling Problems: In scheduling tasks, where tasks represent vertices and conflicts between tasks represent edges, the Four Color Theorem guarantees that no more than four time slots (colors) are needed to schedule tasks that conflict with each other.
• Frequency Assignment: In telecommunications, when assigning frequencies to transmitters, the theorem can be applied to ensure that adjacent transmitters do not interfere with each other by using the same frequency.
• Graph Coloring Algorithms: The theorem has also influenced the development of graph coloring algorithms used in computer science, such as those for register allocation in compilers, where variables in a program are represented as vertices and the goal is to assign registers (colors) to variables in a way that avoids conflicts.

Limitations of Four Color Theorem

Although the Four Color Theorem is a major result in graph theory, it has certain limitations and extensions that are worth mentioning:

• Limited to Planar Graphs: The theorem applies only to planar graphs. For graphs that are not planar, the theorem does not provide any guarantees about the number of colors needed for coloring.
• Complex Proof: The original proof of the theorem was highly complex, requiring the use of a computer to check thousands of configurations. While the theorem itself is simple to state, the proof is not easily accessible to all mathematicians due to its computational nature.
• Generalizations: There are many generalizations of the Four Color Theorem for specific types of graphs. For example, the chromatic number of some graphs may be larger than four, depending on the structure of the graph.

Generalizations and Extensions

Since the proof of the Four Color Theorem, researchers have explored various extensions and generalizations of the theorem, such as −

• Chromatic Number of Graphs: The chromatic number of a graph is the smallest number of colors needed to color a graph such that no two adjacent vertices share the same color. The Four Color Theorem is a specific case of the general problem of determining the chromatic number of a planar graph.
• Five Color Theorem: For non-planar graphs, the Five Color Theorem provides a generalization, stating that any graph can be colored with no more than five colors. While it is not as widely applicable as the Four Color Theorem, it provides details into graph coloring problems.
• Other Colorability Results: Further research has led to other results related to graph colorability, such as the concept of coloring graphs with specific constraints (e.g., vertex or edge coloring) and the study of colorings in hypergraphs.

Relation to Other Graph Coloring Problems

The Four Color Theorem is a special case of the more general graph coloring problem, which involves assigning the smallest number of colors to a graph such that no two adjacent vertices share the same color.

In this broader context, the Four Color Theorem provides a specific solution for planar graphs, but other types of graphs (such as non-planar graphs) may require different methods.

For example, the chromatic number of a graph is the minimum number of colors needed to color a graph. For non-planar graphs, the chromatic number can be much larger than four, and in some cases, there may be no upper bound on the chromatic number. However, for planar graphs, the Four Color Theorem provides a clear upper bound.