Graph Theory - Traversability

---

---

Graph Traversability

Graph traversability refers to the ability to visit all edges or vertices of a graph under specific conditions. It determines whether a graph can be fully explored without repetition or without lifting a pen, as in the famous "Seven Bridges of Knigsberg" problem.

What is Traversability?

Traversability in graph theory examines whether a graph can be completely traversed under given constraints. It helps answer questions like −

• Can all edges of a graph be visited exactly once? (Eulerian Path and Circuit)
• Can all vertices of a graph be visited exactly once? (Hamiltonian Path and Circuit)
• Does a valid path exist between two points?

Eulerian Graphs - Edge Traversability

A graph is called Eulerian if it contains an Eulerian path or circuit. These concepts define whether all edges can be traversed exactly once.

Eulerian Path

An Eulerian Path is a path that visits every edge of the graph exactly once. It may start and end at different vertices.

• A graph has an Eulerian path if it has exactly 0 or 2 vertices with an odd degree.
• If there are exactly 2 odd-degree vertices, the path starts at one and ends at the other.

Eulerian Circuit

An Eulerian Circuit is a closed Eulerian path that starts and ends at the same vertex.

• A graph has an Eulerian circuit if all vertices have even degrees and the graph is connected.

Consider the following graph −

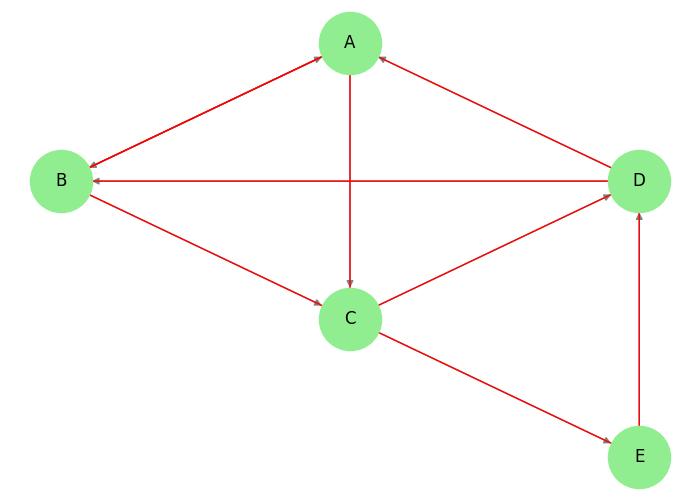
Eulerian Circuit: A  C  E  D  B  C  D  A  B  A
Eulerian Path: A  C  E  D  B  C  D  A  B  A

Here, for Eulerian Circuit, the traversal starts at A. Every edge is visited exactly once. The traversal returns to A, forming a closed loop.

Hamiltonian Graphs - Vertex Traversability

A graph is called Hamiltonian if it contains a Hamiltonian path or circuit. These concepts define whether all vertices can be traversed exactly once.

Hamiltonian Path

A Hamiltonian Path is a path that visits each vertex of a graph exactly once, but does not necessarily return to the starting vertex.

• There is no simple rule like Eulerian graphs to determine if a Hamiltonian path exists.

Hamiltonian Circuit

A Hamiltonian Circuit is a Hamiltonian path that forms a closed cycle by returning to the starting vertex.

• A Hamiltonian circuit exists if a Hamiltonian path can be extended into a cycle.

Consider the following graph −

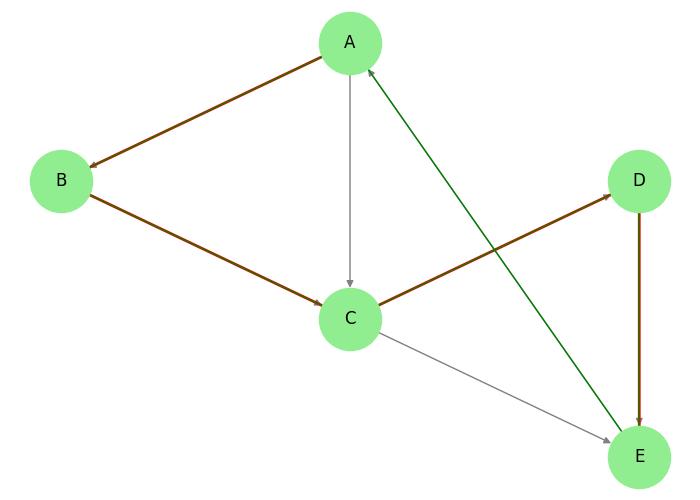
Hamiltonian Path: A  B  C  D  E
Hamiltonian Circuit: A  B  C  D  E  A

Connectedness and Traversability

A graph must be connected to be traversable under Eulerian or Hamiltonian rules −

• A graph is connected if there is a path between every pair of vertices.
• A graph with multiple disconnected components is not traversable under Eulerian or Hamiltonian rules.

Application of Traversability

Following are the real life applications of graph traversabiliy −

• Network Routing - Ensuring efficient traversal of networks.
• Robotics - Programming robots to cover a space efficiently.
• DNA Sequencing - Determining the correct order of genetic sequences.
• Traveling Salesman Problem - Finding the shortest path to visit multiple locations.