Graph Theory - Planar Graphs

---

---

Planar Graphs in Graph Theory

A planar graph is a graph that can be embedded in the plane, meaning it can be drawn on a flat surface such that no two edges cross each other.

In other words, a planar graph can be represented without any edges intersecting, except at their endpoints.

Properties of Planar Graphs

Planar graphs have several properties that are important for analyzing and understanding their structure. These properties are helpful in graph drawing, algorithm design, and practical applications −

No Edge Crossings

The most defining property of a planar graph is that it can be drawn on a plane without any of its edges crossing. This means that the graph can be represented such that no two edges share any points other than their vertices.

Euler's Formula

One of the most important theorems for planar graphs is Euler's formula, which relates the number of vertices (V), edges (E), and faces (F) in a connected planar graph −

V - E + F = 2

This formula holds for all connected planar graphs, and it helps in proving whether a graph is planar. It provides an important constraint for planar graphs, linking the number of vertices, edges, and regions (faces) formed by the edges.

Handshaking Lemma for Planar Graphs

In any graph, the sum of the degrees of all vertices is twice the number of edges. In planar graphs, this lemma implies that the sum of the vertex degrees is bounded, which can help in analyzing the graph's properties and finding efficient algorithms for planar graphs.

Face Structure

In a planar graph, a face is a region bounded by edges. In a simple planar graph, the outer region is also considered a face. Understanding the face structure of a planar graph is useful for solving problems related to graph drawing and network optimization.

Planarity and Subgraphs

If a graph is planar, every subgraph of the graph is also planar. However, the converse is not necessarily true. Subgraphs of non-planar graphs may or may not be planar. This property helps identify whether specific subgraphs in a larger graph could be planar, leading to simpler analysis.

Planar Graphs and Degree of Vertices

In planar graphs, there are certain constraints on the degree of vertices. For example, a simple planar graph with no multi-edges or self-loops must have at least three vertices with degree at most five.

Simple Planar Graphs

A simple planar graph is a graph with no multiple edges or loops. Simple planar graphs are easier to analyze, and their properties are more straightforward compared to graphs that allow self-loops or multiple edges. Many theorems and algorithms in graph theory are specifically designed for simple planar graphs.

Planar Graph Drawing

Planar graphs are often used in practical applications, such as map drawing, circuit design, and network analysis. Drawing a planar graph without edge crossings is essential for visualizing the structure and properties of the graph.

Graph Embedding

Graph embedding is the process of drawing a planar graph on a surface, such that no edges cross. This is an essential part of graph visualization techniques, and several algorithms exist to ensure that a graph can be embedded on a plane while maintaining planarity.

Kuratowski's Theorem

Kuratowski's theorem states that a graph is planar if and only if it does not contain a subgraph that is a subdivision of either the complete graph K₅ or the complete bipartite graph K_3,4. These two graphs, K₅ and K_3,4, are non-planar graphs and act as forbidden subgraphs for planarity.

Planar Graph Algorithms

There are many algorithms designed to solve problems involving planar graphs, such as determining whether a graph is planar, finding a planar embedding, and coloring planar graphs.

Planarity Testing

One of the key problems in planar graph theory is determining whether a given graph is planar. There are various algorithms for this task, such as −

• Hopcroft and Tarjan's Planarity Test: This algorithm determines whether a graph is planar using depth-first search and is one of the most famous planarity testing algorithms.
• Kurth's Planarity Algorithm: Another algorithm for testing planarity based on graph traversal and cycle detection.

Graph Coloring

Graph coloring in planar graphs refers to the assignment of colors to the faces or vertices of the graph such that no two adjacent faces (or vertices) share the same color. The Four Color Theorem states that every planar graph can be colored using at most four colors, which is a major result in graph theory.

Planar Graph Embedding and Visualization

Embedding a planar graph involves positioning the vertices in a two-dimensional space such that no edges intersect. Several graph visualization tools and algorithms, such as force-directed algorithms and circular layouts, help in visualizing planar graphs in an aesthetically pleasing way while maintaining their planarity.

Applications of Planar Graphs

Planar graphs are used in various real-world applications where the spatial arrangement of elements matters. Here are some key applications −

Geographic Mapping and Cartography

Planar graphs are extensively used in geographic mapping, where locations (vertices) and connections (edges) need to be represented on a two-dimensional surface. These graphs help in route planning, location mapping, and network design without overlap or crossing lines.

Circuit Design

In electrical engineering, planar graphs are used to design circuits where connections between components need to be represented without overlapping wires. Planarity constraints ensure that circuits are efficiently laid out and manufacturable without crossing lines.

Network Design and Optimization

Planar graphs are useful in designing communication networks, such as wireless networks, where the connections (edges) between nodes (vertices) should be planned in a way that avoids interference and allows routing.

Resource Allocation

Planar graphs are applied in resource allocation problems, where tasks or resources (represented by vertices) need to be connected in a non-overlapping way. This is especially important in logistics, transport, and supply chain management.

Topological Map Design

Planar graphs are used to represent topological maps, such as transportation routes, utility networks, and social connections, where the primary concern is avoiding edge crossings and ensuring clarity in the representation of the network.

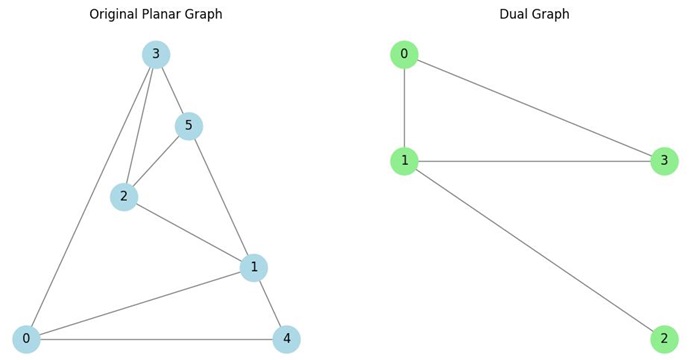
Duality of Planar Graphs

For every planar graph, there exists a dual graph where the vertices of the dual graph represent the faces of the original graph, and the edges of the dual graph represent the shared boundaries between the faces of the original graph. This concept is used in various applications like network flow problems and optimization.

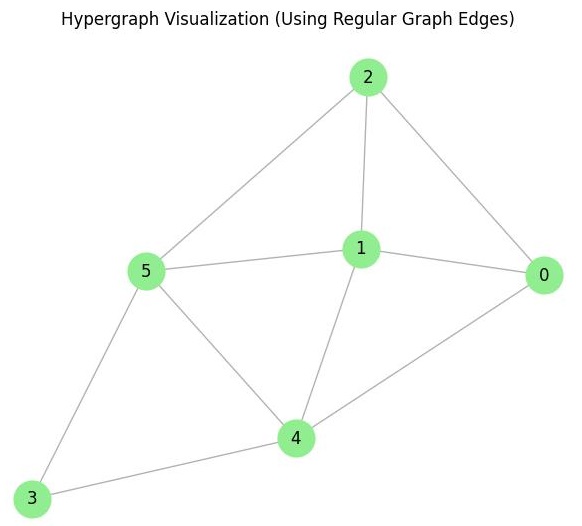
Planar Graphs and Hypergraphs

Hypergraphs are generalizations of graphs where edges can connect more than two vertices. Planar graphs are sometimes studied in relation to hypergraphs, especially in cases where the edges represent relationships between multiple vertices, such as in network analysis and multi-agent systems.

Planar Graph Minors

In graph theory, planar graph minors refer to a concept where a graph is considered a "minor" of a planar graph if it can be obtained from the planar graph by a series of edge contractions, edge deletions, and vertex deletions.

Essentially, a graph G is a minor of a planar graph H if G can be formed by modifying H in these specific ways, without violating the properties of a planar graph.

Key characteristics of Planar Graph Minors are −

• Edge Contraction: This involves merging two adjacent vertices into a single vertex, while keeping the edges incident to both vertices intact.
• Edge and Vertex Deletion: These remove edges and vertices from the graph, effectively simplifying its structure.
• Preservation of Planarity: The graph minors concept focuses on preserving the planar nature of the graph after performing the contraction and deletion operations.