Graph Theory - Chromatic Polynomial

Quiz

Chromatic Polynomial

The chromatic polynomial of a graph expresses the number of ways a graph can be colored using a specific number of colors, while ensuring that no two adjacent vertices share the same color.

It provides a detail into the coloring properties of a graph and is useful for understanding the behavior of graph colorings with respect to different numbers of colors.

Mathematically, the chromatic polynomial is denoted as −

P(G, x) = the number of ways to color G with x colors

The formula for the chromatic polynomial P(G, x) of a simple graph G is given as −

P(G, x) = (x - 1)^|V| ∏_{v ∈ V(G)} (x - deg(v))

Where,

P(G, x) is the chromatic polynomial of graph G.
|V| is the number of vertices in the graph G.
deg(v) is the degree of a vertex v in the graph.
x represents the number of colors available.

This formula calculates the number of ways to color the vertices of the graph such that no two adjacent vertices have the same color, using x colors.

For example,

Chromatic Polynomial for x=3: P(G, 3) = 6
Chromatic Polynomial for x=4: P(G, 4) = 24
Chromatic Polynomial for x=5: P(G, 5) = 60

In simpler terms, it gives the number of valid colorings possible with x colors, considering the graph's structure and adjacency constraints.

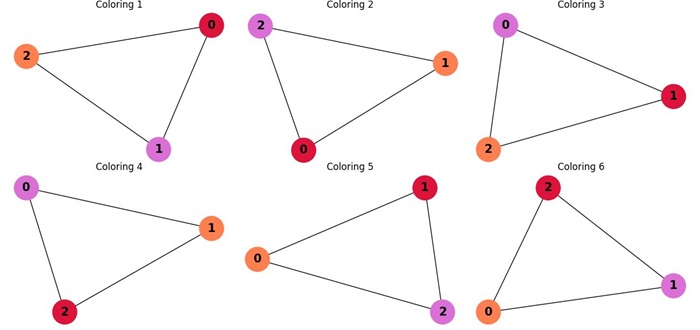
The above image represents the chromatic polynomial of a triangular graph K₃.

Properties of Chromatic Polynomial

The chromatic polynomial has several important properties that help in analyzing its behavior and solving graph coloring problems −

Evaluation at x = 0: The chromatic polynomial evaluated at x = 0 represents the number of ways to color the graph with zero colors. This value is always 0, as it is impossible to color a graph with no colors.
Evaluation at x = 1: The chromatic polynomial evaluated at x = 1 counts the number of ways to color the graph with exactly one color. If the graph is not a complete graph, the result is 0, as it is impossible to color the graph with only one color if there are any edges.
Evaluation at x = 2: The chromatic polynomial evaluated at x = 2 counts the number of ways to color the graph with exactly two colors. This value is particularly useful for bipartite graphs, as a bipartite graph is 2-colorable, and the chromatic polynomial at x = 2 will give a non-zero result.
Degree of the Polynomial: The degree of the chromatic polynomial is equal to the number of vertices in the graph. For graphs with n vertices, the chromatic polynomial will be a polynomial of degree n.
Monotonicity: The chromatic polynomial is a decreasing function of x, meaning that as the number of colors increases, the number of valid colorings also increases.

Applications of Chromatic Polynomial

The chromatic polynomial is used in various applications, such as −

Graph Coloring: The chromatic polynomial helps in understanding the number of valid colorings for a graph, which is useful in solving graph coloring problems, such as scheduling, task allocation, and resource management.
Counting Colorings: The chromatic polynomial can be used to count the number of distinct ways to color a graph using a specific number of colors, which is important in combinatorics and optimization problems.
Planar Graphs: For planar graphs, the chromatic polynomial is used to analyze the structure and behavior of graph colorings, especially in cases where the Four Color Theorem applies.
Graph Theory Research: The chromatic polynomial is an important tool in graph theory research, helping to explore the properties of graphs, including their structure, coloring properties, and relationship to other graph invariants.

Let us look at some examples to understand how to calculate the chromatic polynomial for various types of graphs.

Chromatic Polynomial of Complete Graph

A complete graph K_n is a graph where every pair of vertices is connected by an edge. The chromatic polynomial of a complete graph with n vertices is given by −

P(Kn, x) = x(x - 1)(x - 2)...(x - n + 1)

This is because, in a complete graph, each vertex must be assigned a unique color to ensure that no two adjacent vertices share the same color. Thus, the chromatic polynomial counts the number of ways to assign unique colors to the vertices of the complete graph.

For example, if we have a complete graph with 4 vertices (K₄), the chromatic polynomial is −

P(K4, x) = x(x - 1)(x - 2)(x - 3)

Where, x is the number of colors −

Number of ways to color K4 with 4 colors: 24
Number of ways to color K4 with 5 colors: 120
Number of ways to color K4 with 6 colors: 360

The above image represents the chromatic polynomial of a complete graph K₄.

Chromatic Polynomial of a Bipartite Graph

A bipartite graph is a graph whose vertices can be divided into two disjoint sets, such that no two vertices within the same set are adjacent. The chromatic polynomial of a bipartite graph is always 2, because a bipartite graph can be colored with exactly two colors. This applies to all bipartite graphs, regardless of their size or structure.

For example, consider a bipartite graph with two sets of vertices: {A, B} and {1, 2}. The edges are: A-1, B-2. The chromatic polynomial of this graph is −

P(G, x) = 2

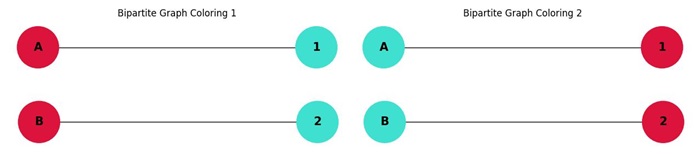
Chromatic Polynomial of a Cycle (C_n)

A cycle graph C_n is a graph with n vertices connected in a closed loop, where each vertex is adjacent to two other vertices. The chromatic polynomial of a cycle graph is given by −

P(Cn, x) = (x - 1)ⁿ + (-1)ⁿ

This polynomial counts the number of valid colorings for the cycle graph, ensuring that no adjacent vertices share the same color.

For example, if we have a cycle graph with 4 vertices (C₄), the chromatic polynomial is −

P(C4, x) = (x - 1)⁴ + (-1)⁴

Here, x is the number of colours used −

Number of ways to color C4 with 2 colors: 2
Number of ways to color C4 with 3 colors: 17

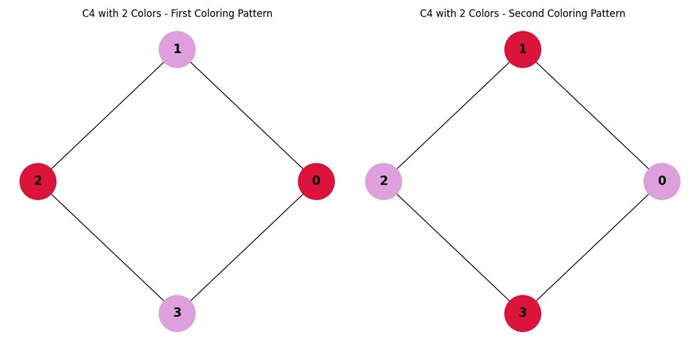
The above image visualizes the chromatic polynomial of a cycle graph "C4" with 2 colors.

Similarly, for C₅ (5 vertices):

Number of ways to color C5 with 2 colors: 0 [P(C₅, 2 = (2-1)⁵ + (-1)⁵]
Number of ways to color C5 with 3 colors: 31

Challenges in Chromatic Polynomial

Determining the chromatic polynomial of a graph can be a complex task, particularly for graphs with many vertices and edges. Some of the major challenges are −

Complexity for Large Graphs: For large graphs, calculating the chromatic polynomial can be demanding, as it involves considering many possible colorings and evaluating polynomial functions.
Non-trivial Graphs: For non-trivial graphs with intricate structures, finding an explicit expression for the chromatic polynomial may not be easy, and may require advanced techniques.
Inexact Formulas: In some cases, approximating the chromatic polynomial or finding bounds for it can be difficult, especially for graphs with complex topologies.

Print Page