Graph Theory - Johnson's Algorithm

Previous
Quiz
Next

Johnson's Algorithm

Johnson's algorithm is used for finding the shortest paths between all pairs of vertices in a weighted, directed graph. It is particularly useful for graphs with non-negative weights and is an alternative to the Floyd-Warshall algorithm when the graph has sparse edges.

This algorithm can handle graphs with negative weights, but it requires an additional preprocessing step to detect negative weight cycles, which it cannot handle.

Johnson's algorithm works by performing a series of individual shortest-path calculations from each vertex using a single-source shortest-path algorithm, such as Dijkstra's algorithm. By using reweighting techniques, Johnson's algorithm ensures that all edges have non-negative weights, allowing Dijkstra's algorithm to be used efficiently.

Overview of Johnson's Algorithm

Johnson's algorithm combines two major components −

  • Reweighting of edges: A transformation is applied to the graph to eliminate negative weights by assigning a new weight to each edge.
  • Shortest-path calculations using Dijkstra's algorithm: After reweighting, Dijkstra's algorithm is used to calculate the shortest paths from each vertex to every other vertex.

While the Floyd-Warshall algorithm has a time complexity of O(V3), Johnson's algorithm has a time complexity of O(V2 log V + VE), where V is the number of vertices and E is the number of edges in the graph. This makes Johnson's algorithm more efficient for sparse graphs with fewer edges.

Steps of Johnson's Algorithm

The Johnson's algorithm proceeds in the following steps −

  • Step 1: Add a new vertex: Introduce a new vertex q to the graph and add edges from q to every other vertex with weight 0. This new vertex will be used for the reweighting process.
  • Step 2: Apply Bellman-Ford algorithm: Run the Bellman-Ford algorithm from vertex q to calculate the shortest paths from q to all other vertices. This step helps in detecting negative weight cycles.
  • Step 3: Reweight edges: Once the shortest path distances from q to every other vertex are known, reweight the edges of the original graph using the formula: weight(u, v) = original weight(u, v) + h(u) - h(v), where h(u) is the shortest path distance from q to vertex u.
  • Step 4: Run Dijkstra's algorithm: After reweighting the edges, use Dijkstra's algorithm for each vertex in the graph to compute the shortest paths from each vertex to every other vertex.
  • Step 5: Recover the original weights: After executing Dijkstra's algorithm, the shortest path results are adjusted back to their original values by subtracting the reweighting factors.

Example of Johnson's Algorithm

Consider the following weighted directed graph −

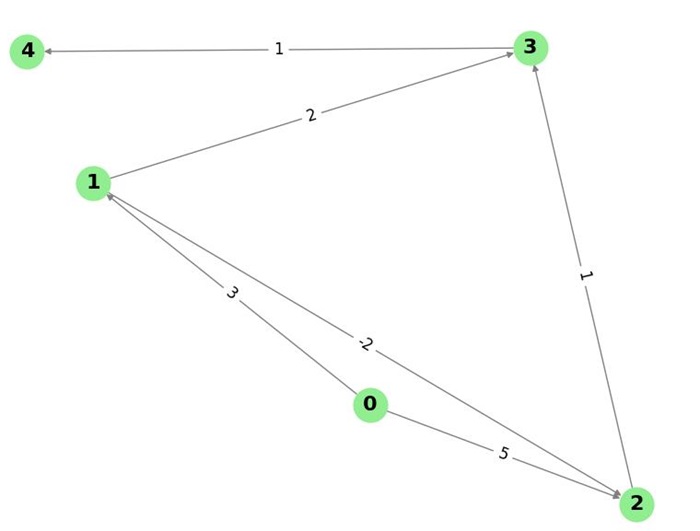
Johnson's Algorithm

The adjacency list representation of the graph is as follows −

graph = {
   0: [(1, 3), (2, 5)],
   1: [(2, -2), (3, 2)],
   2: [(3, 1)],
   3: [(4, 1)],
   4: []
}

Let us apply Johnson's algorithm to find the shortest paths between all pairs of vertices in this graph. Here, we will follow each step of the process, from adding a new vertex to the reweighting, executing Dijkstra's algorithm, and recovering the original weights.

Step 1: Add a New Vertex

We add a new vertex q to the graph and connect it to all other vertices with edges of weight 0. The updated graph will look as follows −

graph_with_q = {
   'q': [(0, 0), (1, 0), (2, 0), (3, 0), (4, 0)],
   0: [(1, 3), (2, 5)],
   1: [(2, -2), (3, 2)],
   2: [(3, 1)],
   3: [(4, 1)],
   4: []
}

Step 2: Apply Bellman-Ford Algorithm

Next, we run the Bellman-Ford algorithm from the newly added vertex q to calculate the shortest distances from q to every other vertex.

The Bellman-Ford algorithm helps detect negative weight cycles and computes the shortest paths to each vertex. After running Bellman-Ford, we get the shortest path distances from q to all other vertices:

h = {
   'q': 0,
   0: 0,
   1: 3,
   2: 5,
   3: 6,
   4: 7
}

Step 3: Reweight the Edges

We then reweight the edges using the formula −

new_weight(u, v) = original_weight(u, v) + h(u) - h(v)

This ensures that all edge weights are non-negative. The reweighted graph looks like this:

reweighted_graph = {
   0: [(1, 0), (2, 3)],
   1: [(2, -5), (3, 1)],
   2: [(3, -5)],
   3: [(4, -6)],
   4: []
}

Step 4: Run Dijkstra's Algorithm

Now that all edge weights are non-negative, we can use Dijkstra's algorithm to find the shortest paths from each vertex to all other vertices. We will run Dijkstra's algorithm for each vertex in the graph:

import heapq

def dijkstra(graph, start):
   dist = {vertex: float('inf') for vertex in graph}
   dist[start] = 0
   priority_queue = [(0, start)]
    
   while priority_queue:
      current_distance, current_vertex = heapq.heappop(priority_queue)
      
      if current_distance > dist[current_vertex]:
         continue
        
      for neighbor, weight in graph[current_vertex]:
         distance = current_distance + weight
         if distance < dist[neighbor]:
            dist[neighbor] = distance
            heapq.heappush(priority_queue, (distance, neighbor))
                
   return dist

# Running Dijkstra for all vertices
all_pairs_shortest_paths = {}
for vertex in graph_with_q:
   all_pairs_shortest_paths[vertex] = dijkstra(reweighted_graph, vertex)
    
print(all_pairs_shortest_paths)

Step 5: Recover the Original Weights

After running Dijkstra's algorithm, we adjust the results back to the original edge weights by subtracting the reweighting factors:

adjusted_paths = {}
for start in all_pairs_shortest_paths:
   adjusted_paths[start] = {}
   for end in all_pairs_shortest_paths[start]:
      adjusted_paths[start][end] = all_pairs_shortest_paths[start][end] + h[end] - h[start]

print(adjusted_paths)

Complete Implementation

Following is a Python complete implementation of Johnson's algorithm −

graph = {
   0: [(1, 3), (2, 5)],
   1: [(2, -2), (3, 2)],
   2: [(3, 1)],
   3: [(4, 1)],
   4: []
}
graph_with_q = {
   'q': [(0, 0), (1, 0), (2, 0), (3, 0), (4, 0)],
   0: [(1, 3), (2, 5)],
   1: [(2, -2), (3, 2)],
   2: [(3, 1)],
   3: [(4, 1)],
   4: []
}
h = {
   'q': 0,
   0: 0,
   1: 3,
   2: 5,
   3: 6,
   4: 7
}
reweighted_graph = {
   'q': [(0, 0), (1, 0), (2, 0), (3, 0), (4, 0)],
   0: [(1, 0), (2, 3)],
   1: [(2, -5), (3, 1)],
   2: [(3, -5)],
   3: [(4, -6)],
   4: []
}

import heapq

def dijkstra(graph, start):
   dist = {vertex: float('inf') for vertex in graph}
   dist[start] = 0
   priority_queue = [(0, start)]
    
   while priority_queue:
      current_distance, current_vertex = heapq.heappop(priority_queue)
      
      if current_distance > dist[current_vertex]:
         continue
        
      for neighbor, weight in graph[current_vertex]:
         distance = current_distance + weight
         if distance < dist[neighbor]:
            dist[neighbor] = distance
            heapq.heappush(priority_queue, (distance, neighbor))
                
   return dist

# Printing the Original Graph
print("Original Graph::")
print(graph)

# Printing the Reweighted Graph
print("\nReweighted Graph::")
print(reweighted_graph)

# Running Dijkstra for all vertices
all_pairs_shortest_paths = {}
for vertex in graph_with_q:
   all_pairs_shortest_paths[vertex] = dijkstra(reweighted_graph, vertex)

# Printing All Pairs Shortest Paths
print("\nAll Pairs Shortest Paths:")
print(all_pairs_shortest_paths)

# Adjusting the shortest paths using the potential function h
adjusted_paths = {}
for start in all_pairs_shortest_paths:
   adjusted_paths[start] = {}
   for end in all_pairs_shortest_paths[start]:
      adjusted_paths[start][end] = all_pairs_shortest_paths[start][end] + h[end] - h[start]

# Printing Adjusted Shortest Paths
print("\nAdjusted Shortest Paths:")
print(adjusted_paths)

This produces the following output −

Original Graph::
{0: [(1, 3), (2, 5)], 1: [(2, -2), (3, 2)], 2: [(3, 1)], 3: [(4, 1)], 4: []}

Reweighted Graph::
{'q': [(0, 0), (1, 0), (2, 0), (3, 0), (4, 0)], 0: [(1, 0), (2, 3)], 1: [(2, -5), (3, 1)], 2: [(3, -5)], 3: [(4, -6)], 4: []}
All Pairs Shortest Paths:
{'q': {'q': 0, 0: 0, 1: 0, 2: -5, 3: -10, 4: -16}, 0: {'q': inf, 0: 0, 1: 0, 2: -5, 3: -10, 4: -16}, 1: {'q': inf, 0: inf, 1: 0, 2: -5, 3: -10, 4: -16}, 2: {'q': inf, 0: inf, 1: inf, 2: 0, 3: -5, 4: -11}, 3: {'q': inf, 0: inf, 1: inf, 2: inf, 3: 0, 4: -6}, 4: {'q': inf, 0: inf, 1: inf, 2: inf, 3: inf, 4: 0}}

Adjusted Shortest Paths:
{'q': {'q': 0, 0: 0, 1: 3, 2: 0, 3: -4, 4: -9}, 0: {'q': inf, 0: 0, 1: 3, 2: 0, 3: -4, 4: -9}, 1: {'q': inf, 0: inf, 1: 0, 2: -3, 3: -7, 4: -12}, 2: {'q': inf, 0: inf, 1: inf, 2: 0, 3: -4, 4: -9}, 3: {'q': inf, 0: inf, 1: inf, 2: inf, 3: 0, 4: -5}, 4: {'q': inf, 0: inf, 1: inf, 2: inf, 3: inf, 4: 0}}
Johnson's Algorithm

Complexity of Johnson's Algorithm

The time complexity of Johnson's algorithm is O(V2 log V + VE), where V is the number of vertices and E is the number of edges in the graph. The most time-consuming part is running Dijkstra's algorithm for each vertex, which has a time complexity of O(E log V) for each run.

The space complexity of Johnson's algorithm is O(V2 + E) because it requires storing the adjacency list representation of the graph, the reweighted graph, and the distances computed by Dijkstra's algorithm.

Applications of Johnson's Algorithm

Johnson's algorithm has various applications, including:

  • All-Pairs Shortest Path: Johnson's algorithm is used to find the shortest paths between all pairs of vertices, especially in sparse graphs.
  • Network Analysis: It is useful in network routing problems where we need to compute the shortest paths between multiple nodes in a network.
  • Optimal Pathfinding: It is used in situations where finding the optimal path from multiple sources to multiple destinations is required, such as in transportation or logistics problems.
  • Pathfinding in Large Graphs: Johnson's algorithm is useful in handling large graphs where the number of edges is much smaller than the square of the number of vertices.
Print Page
Previous
Next
Advertisements