Graph Theory - Total Coloring

---

---

Total Coloring

Total coloring in graph theory refers to assigning colors to both the vertices and edges of a graph such that no two adjacent vertices, no two adjacent edges, and no edge and its incident vertices share the same color.

The goal is to find the minimum number of colors required to color the entire graph (both vertices and edges) while sticking to these constraints.

Properties of Total Coloring

Total coloring has several important properties that define its challenges and solutions. Some of the important properties are −

• Coloring Constraints: The primary constraint in total coloring is that no two adjacent vertices, no two adjacent edges, and no edge and its incident vertices should share the same color. These constraints ensure the distinction between different graph elements.
• Total Chromatic Number: The total chromatic number of a graph is the minimum number of colors required to color both the vertices and edges of the graph, sticking to the coloring constraints.
• Upper and Lower Bounds: Similar to edge coloring, total coloring has upper and lower bounds on the chromatic number, which can help estimate the required number of colors.

Types of Total Coloring

There are different types of total coloring techniques that vary depending on the properties of the graph. Some of the common types are as follows −

• Proper Total Coloring: This is the basic type of total coloring, where the color assignments must ensure that no two adjacent vertices or edges, or an edge and its incident vertices, share the same color.

• Perfect Total Coloring: A perfect total coloring is one in which the total chromatic number equals the maximum degree of the graph. This type of coloring provides an optimal solution, where the number of colors used is minimal.

• Balanced Total Coloring: This coloring type minimizes the number of times any color is used and ensures that the colors are uniformly distributed across the vertices and edges.

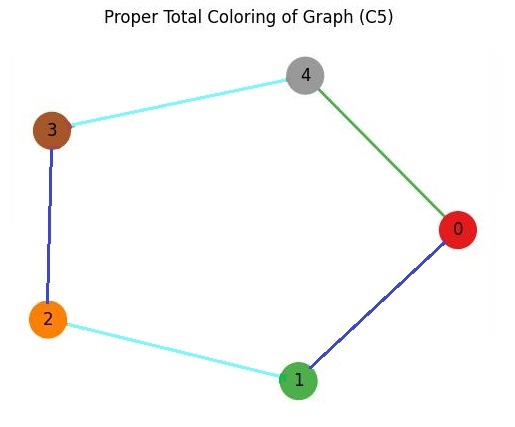
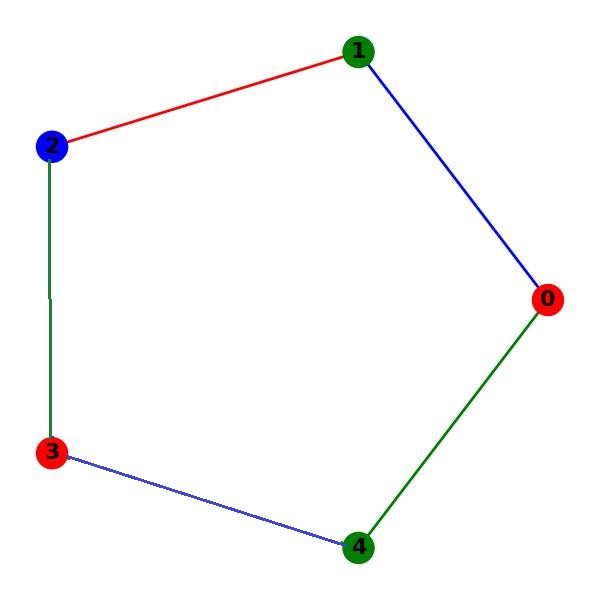
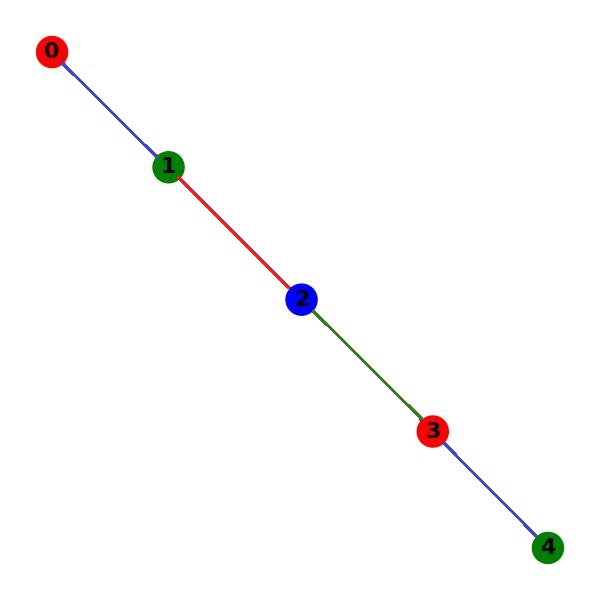
Total Chromatic Number

The total chromatic number is the minimum number of colors needed to color both the vertices and edges of a graph while satisfying the coloring constraints. This number is important as it helps determine the optimal solution for total coloring problems.

The total chromatic number, denoted as X'(G), is related to the maximum degree of the graph, but it is generally greater than or equal to the chromatic number of the graph or the chromatic index.

For many graphs, the total chromatic number is approximately equal to the maximum degree of the graph plus one.

Upper Bound on Total Coloring

The upper bound on the total chromatic number provides a maximum limit on the number of colors required to color both the vertices and edges of a graph. For any graph, the upper bound on the total chromatic number is generally less than or equal to the maximum degree of the graph plus two.

This bound is derived from the fact that in the worst-case scenario, both the vertices and edges must be colored distinctly, resulting in an upper bound of at most the maximum degree plus two, as outlined in various theorems on total coloring.

In many cases, this upper bound is useful for estimating the required number of colors without explicitly calculating the exact total chromatic number.

Lower Bound on Total Coloring

The lower bound on the total chromatic number represents the minimum number of colors required for the total coloring of a graph. This bound is often based on the structure and degree of the graph.

The lower bound is generally equal to the maximum degree of the graph plus one, meaning that at least that many colors are required for a valid total coloring. This lower bound is important for understanding the limitations of total coloring in various graphs.

Total Coloring and Graph Parameters

Total coloring is closely related to other graph parameters, such as vertex coloring, edge coloring, and chromatic number. The relationship between total coloring and these parameters provides details into the complexity of coloring problems. Some important relationships are −

• Vertex Coloring vs. Total Coloring: Vertex coloring involves coloring only the vertices such that no two adjacent vertices have the same color, while total coloring deals with both vertices and edges. The two problems are related but have different constraints.
• Chromatic Number vs. Total Chromatic Number: The chromatic number is the minimum number of colors required to color the vertices of a graph, while the total chromatic number is the minimum number of colors required to color both the vertices and edges.

Total Coloring and Degree Constraints

Degree constraints plays an important role in determining the total chromatic number of a graph. The degree of a vertex is the number of edges incident to that vertex, and it influences how many colors are needed for proper total coloring.

According to a well-known result, the total chromatic number of a graph is generally bounded by the maximum degree of the graph plus two. The degree constraints are directly related to the number of colors required to ensure that the coloring rules are satisfied.

Total Coloring of Special Graphs

Special graphs, such as bipartite graphs, planar graphs, and complete graphs, have specific properties that influence their total coloring. For example −

• Bipartite Graphs: In bipartite graphs, the total chromatic number is equal to the maximum degree of the graph plus one. Since there are no edges within the same set, this simplifies the coloring process.
• Planar Graphs: Planar graphs, which can be drawn on a plane without edges crossing, tend to have a lower total chromatic number compared to non-planar graphs. The total chromatic number of planar graphs is bounded by a fixed value.
• Complete Graphs: In complete graphs, where every pair of distinct vertices is connected by an edge, the total chromatic number is high. Specifically, for complete graphs with an even number of vertices, the total chromatic number is equal to the number of vertices.

Total Coloring in Non-Planar Graphs

Non-planar graphs, which cannot be drawn on a plane without edges crossing, present challenges in terms of total coloring. The total chromatic number of non-planar graphs can often be higher than that of planar graphs due to their more complex structure.

However, even in non-planar graphs, the total chromatic number is bounded by the maximum degree of the graph plus two, as suggested by various total coloring theorems. This upper bound helps in estimating the total chromatic number for non-planar graphs.

For example, consider the complete graph K₅, which is non-planar. The total chromatic number of K₅ is 6 because it has 5 vertices, and each vertex is connected to all others.

Total Coloring Algorithms

We can use various algorithms to solve total coloring problems, each with different approaches to coloring vertices and edges. Some of the major algorithms are as follows −

• Greedy Total Coloring Algorithm: This algorithm colors vertices and edges sequentially, choosing the smallest available color for each element.
• Backtracking Algorithm: The backtracking algorithm explores all possible colorings, backtracking when a conflict arises. It is used for exhaustive search but can be expensive.
• Hybrid Algorithms: Hybrid algorithms combine various techniques, such as greedy coloring and backtracking, to solve the total coloring problem more efficiently for different types of graphs.

Applications of Total Coloring

Total coloring has several practical applications in various domains, such as −

• Telecommunications: Total coloring is used in frequency assignment problems, where both the stations (vertices) and the transmission paths (edges) must be assigned different frequencies to avoid interference.
• Scheduling: In scheduling, total coloring helps assign time slots to tasks and resources, ensuring that no two tasks sharing a common resource or time slot overlap.
• Network Design: In network design, total coloring is used to optimize resource allocation and ensure communication between devices.

Challenges in Total Coloring

Despite its various applications, total coloring have several challenges, they are −

• Computational Complexity: The problem of finding the total chromatic number is NP-hard in general, meaning there is no known fast algorithm to solve the problem for all types of graphs.
• Large Graphs: As the size of a graph increases, the computational complexity of finding the total chromatic number grows, making it difficult to solve problems for large-scale graphs.
• Graph Structure: The structure of a graph (such as planarity or bipartiteness) can affect the total coloring process, and finding solutions for non-planar or highly connected graphs remains a challenge.