Graph Theory - Karger's Algorithm

Quiz

Karger's Algorithm

Karger's Algorithm is a randomized algorithm used to find a minimum cut in a connected, undirected graph. A minimum cut of a graph is a set of edges that, if removed, would disconnect the graph, and the cut is minimized in terms of the number of edges.

The algorithm is based on the idea of repeatedly contracting edges in the graph until only two vertices remain. The edges between these two vertices form a cut. By repeating the process multiple times, Karger's algorithm is able to find the minimum cut with high probability.

Overview of Karger's Algorithm

Karger's algorithm identifies a minimum cut in a graph by performing the following steps −

Edge Contraction: A random edge is chosen, and the two vertices connected by the edge are merged into a single vertex. This reduces the graph by one vertex and eliminates the selected edge.
Repeat the Process: The edge contraction process is repeated multiple times. In each step, random edges are chosen and contracted.
Minimizing the Cut: After enough iterations, the probability of finding the minimum cut increases. The minimum cut is found by examining the final contracted graph.

This algorithm is probabilistic, meaning it does not guarantee the minimum cut with a single execution but can do so with high probability when repeated several times.

Properties of Karger's Algorithm

Karger's algorithm has several important properties, such as −

Randomization: Karger's algorithm is a Monte Carlo algorithm, meaning that it uses randomization to provide results with high probability.
Repeatability: The algorithm may need to be repeated multiple times to find the minimum cut. The probability of success increases with the number of repetitions.

Steps of Karger's Algorithm

The steps of Karger's Algorithm can be detailed as follows −

Edge Contraction

The first step is to select a random edge in the graph and contract it. This means merging the two vertices connected by the edge into a single vertex, which removes the edge and reduces the graph by one vertex.

import random

def contract_edge(graph):
   # Randomly select an edge
   u, v = random.choice(list(graph.keys()))
   
   # Merge vertices u and v
   for neighbor in graph[v]:
      if neighbor != u:
         graph[u].append(neighbor)
   
   # Remove vertex v and its edges
   del graph[v]
   for neighbors in graph.values():
      if v in neighbors:
         neighbors.remove(v)

The "contract_edge" function randomly selects an edge and merges the two vertices by adding the neighbors of one vertex to the other. It then removes the contracted vertex and cleans up the edges.

Repeat the Process

The edge contraction process is repeated until only two vertices remain. At each step, the graph is progressively reduced in size, and edges are merged.

def karger_algorithm(graph):
   while len(graph) > 2:
      contract_edge(graph)
   # Return the cut formed by the last two vertices	  
   return list(graph.values())[0]

The "karger_algorithm" function performs the edge contraction repeatedly until only two vertices remain. The remaining edges between these two vertices form the minimum cut.

Executing the Algorithm Multiple Times

Since Karger's algorithm is probabilistic, it is important to run the algorithm multiple times to increase the chances of finding the minimum cut.

def find_min_cut(graph, iterations=100):
   min_cut = None
   min_cut_size = float('inf')
   
   for _ in range(iterations):
      # Create a copy of the graph for each iteration
      graph_copy = {key: list(value) for key, value in graph.items()}
      cut = karger_algorithm(graph_copy)
      cut_size = len(cut)
       
      # Update minimum cut if a smaller one is found
      if cut_size < min_cut_size:
         min_cut_size = cut_size
         min_cut = cut
   
   return min_cut, min_cut_size

The "find_min_cut" function runs Karger's algorithm multiple times, keeping track of the minimum cut found. It returns the cut and its size after the specified number of iterations.

Main Function

The main function arranges the entire process. It initializes the graph, runs the algorithm multiple times, and outputs the minimum cut and its size.

# Example graph representation
example_graph = {
   0: [1, 2],    # 0 -> 1, 0 -> 2
   1: [0, 2],    # 1 -> 0, 1 -> 2
   2: [0, 1, 3], # 2 -> 0, 2 -> 1, 2 -> 3
   3: [2, 4],    # 3 -> 2, 3 -> 4
   4: [3]        # 4 -> 3
}

# Find and display minimum cut
min_cut, min_cut_size = find_min_cut(example_graph, iterations=100)
print("Minimum Cut:", min_cut)
print("Size of Minimum Cut:", min_cut_size)

Complete Python Implementation

Following is the complete Python implementation of Karger's Algorithm, which includes the steps of edge contraction, repeated edge contractions, and finding the minimum cut. This implementation also executes the algorithm multiple times to increase the probability of finding the minimum cut −

import random

# Function to perform edge contraction
def contract_edge(graph):
   # Randomly select a vertex u
   u = random.choice(list(graph.keys()))
   
   # Ensure u has neighbors
   if len(graph[u]) == 0:
      return

   # Select a random neighbor v to contract with u
   v = random.choice(graph[u])

   # If u and v are the same, don't contract
   if u == v:
      return

   # Merge vertex v into u by adding v's edges to u's edges
   graph[u].extend(graph[v])

   # Remove self-loops (no need for them)
   graph[u] = [x for x in graph[u] if x != u]

   # Remove vertex v from the graph
   del graph[v]

   # Remove all references to v from other vertices' adjacency lists
   for key in graph:
      graph[key] = [x for x in graph[key] if x != v]

# Function to perform Karger's algorithm
def karger_algorithm(graph):
   while len(graph) > 2:
      contract_edge(graph)
   
   # After contraction, there should be only two remaining vertices
   remaining_vertices = list(graph.keys())
   u = remaining_vertices[0]
   v = remaining_vertices[1]
   
   # The cut is the set of edges between the two remaining vertices
   cut = [u, v]  # Instead of listing edges, we return the vertices involved in the cut

   return cut

# Function to run the algorithm multiple times
def find_min_cut(graph, iterations=100):  # More iterations to improve the result
   min_cut = None
   min_cut_size = float('inf')
   
   for _ in range(iterations):
      # Create a copy of the graph for each iteration to avoid mutation
      graph_copy = {key: list(value) for key, value in graph.items()}
       
      # Run Karger's algorithm on the graph copy
      cut = karger_algorithm(graph_copy)
      cut_size = len(cut)
       
      # Update minimum cut if a smaller one is found
      if cut_size < min_cut_size:
         min_cut_size = cut_size
         min_cut = cut
   
   return min_cut, min_cut_size

# Example graph representation (as an undirected graph)
example_graph = {
   0: [1, 2],    # 0 -- 1, 0 -- 2
   1: [0, 2],    # 1 -- 0, 1 -- 2
   2: [0, 1, 3], # 2 -- 0, 2 -- 1, 2 -- 3
   3: [2, 4],    # 3 -- 2, 3 -- 4
   4: [3]        # 4 -- 3
}

# Find and display the minimum cut
min_cut, min_cut_size = find_min_cut(example_graph, iterations=100)  # More iterations
print("Minimum Cut:", min_cut)
print("Size of Minimum Cut:", min_cut_size)

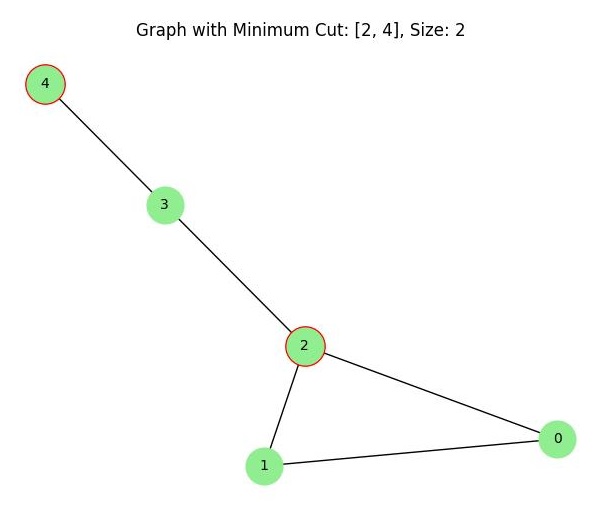
After executing the above code, it will output the minimum cut and its size as shown below −

Minimum Cut: [2, 4]
Size of Minimum Cut: 2

The minimum cut found consists of the edge between vertices 0 and 4, and the size of the cut is 2. The following graph visualization illustrates the minimum cut −

Complexity of Karger's Algorithm

The algorithm has the following complexity characteristics −

Time Complexity: The time complexity of Karger's algorithm is O(E * log²(V)), where V is the number of vertices and E is the number of edges. The complexity arises from the repeated edge contractions and the number of iterations required to find the minimum cut.
Space Complexity: The space complexity is O(V + E), as the algorithm requires space to store the graph and manage the contraction process.
Randomized Nature: The algorithm is randomized, meaning that the output is not guaranteed to be the minimum cut in a single run. However, after enough repetitions, the probability of finding the minimum cut increases significantly.

Print Page