Graph Theory - Force-Directed Methods

---

---

Force-Directed Methods

Force-Directed Methods are techniques used to draw graphs in a way that makes them easy to understand. These methods try to place the nodes (or vertices) so that there are fewer edge crossings and the nodes are spread out evenly.

The idea comes from physics, where forces like attraction and repulsion act on objects. In this case, nodes push away from each other, and edges pull connected nodes together, helping create a clear and balanced graph layout.

• Physical Forces: Nodes in the graph repel each other, and edges act like springs that attract connected nodes.
• Equilibrium: The goal is to reach a state of equilibrium where the forces balance out, resulting in a pleasing layout.
• Efficiency: These methods are particularly effective for un-directed graphs.

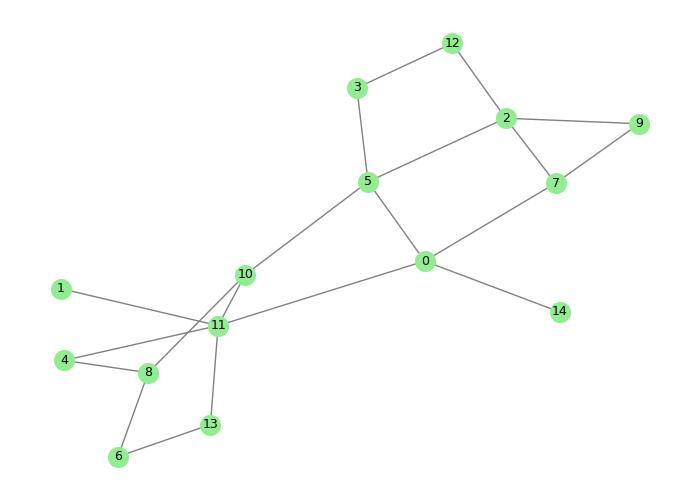
The above image illustrates a force-directed layout with vertices pushed away from each other while edges pull connected vertices closer.

Principle of Force-Directed Methods

The basic idea behind force-directed methods is to treat the graph as a system of physical bodies. Each node in the graph is treated like a charged particle that repels other nodes, while edges act as springs that attract the nodes they connect. This process is iterated until the system reaches a stable configuration.

• Repulsive Force: Nodes experience a repulsive force that pushes them away from each other, reducing node overlaps.
• Attractive Force: Edges act like springs, pulling connected nodes together to maintain their relationship.
• Equilibrium: The layout reaches equilibrium when the forces are balanced, minimizing edge crossings and optimizing the graph layout.

Force-Directed Layout Algorithms

There are different algorithms that use force-directed methods, each applying forces in its own way to arrange the nodes. Here are some common ones −

• Fruchterman-Reingold Algorithm It uses a combination of attractive and repulsive forces to create a balanced layout.
• Spring Layout: In this algorithm, edges are treated like springs. The goal is to reduce the system's energy to make the graph look nice and balanced.
• Force Atlas: Designed for large graphs, this algorithm speeds up the layout process and reduces edge crossings by modifying the spring layout.
• Kamada-Kawai Algorithm: This algorithm minimizes the energy of the graph using attractive forces between nodes based on the graph's distance matrix.

Fruchterman-Reingold Algorithm

The Fruchterman-Reingold algorithm is one of the most popular force-directed algorithms. It works by applying repulsive forces between nodes and attractive forces along the edges. The algorithm keeps adjusting the positions of the nodes until the graph settles into a balanced and stable layout.

The image above demonstrates the result of applying the Fruchterman-Reingold algorithm to a graph.

Force-Directed Layout with Python

Let us create a graph and apply a force-directed layout using Python's networkx and matplotlib libraries.

In the following example, we are applying the spring_layout() function from the networkx library, which implements a force-directed layout to arrange the nodes and edges of the graph −

import networkx as nx
import matplotlib.pyplot as plt

# Create a graph
G = nx.Graph()
G.add_edges_from([(1, 2), (2, 3), (3, 4), (4, 1), (2, 4)])

# Apply the spring layout for force-directed graph drawing
pos = nx.spring_layout(G)

# Draw the graph
nx.draw(G, pos, with_labels=True, node_color="lightgreen", edge_color="blue")

# Display the graph
plt.title("Force-Directed Graph Layout (Fruchterman-Reingold)")
plt.show()

The above code generates a graph using the Fruchterman-Reingold algorithm to determine the positions of nodes, creating an optimal layout for the graph −

Energy Functions and Optimization

In force-directed methods, the layout of the graph is created by reducing the "energy" in the system. This energy is influenced by both attractive forces (pulling nodes together) and repulsive forces (pushing nodes apart).

The goal is to find the arrangement that minimizes the total energy, making the graph balanced and clear. The energy function is a mathematical way to measure how well the forces are working together to create an optimal layout. It often takes the following form −

E = Erepulsive + Eattractive

• Repulsive Energy (E_repulsive): The repulsive energy between two nodes is inversely proportional to the distance between them. The closer two nodes are, the stronger is the repulsive force.
• Attractive Energy (E_attractive): The attractive energy between two nodes connected by an edge is proportional to the distance between them. The nodes are pulled closer to maintain the edge connection.

The algorithm moves the nodes step by step to reduce the energy in the system. It keeps adjusting the positions until the forces (attraction and repulsion) balance out, and the graph reaches a stable, clear layout.

Challenges in Force-Directed Methods

Although force-directed methods work well for many types of graphs, they face some challenges −

• Performance: These algorithms can be slow when dealing with large graphs, especially if there are a lot of nodes and edges.
• Local Minima: Sometimes the algorithm may get stuck in a position that isn't the best possible layout, resulting in a suboptimal graph.
• Edge Crossings: Although the force-directed methods aim to reduce edge crossings, they may still occur, especially in dense graphs.
• Scalability: As the graph size grows, the algorithm takes more time and resources to process, which can make it difficult to use for very large graphs.

Optimizations for Force-Directed Methods

To make force-directed methods work better and faster, several improvements have been proposed −

• Multilevel Layout: This method first simplifies the graph into a smaller version, applies the force-directed technique, and then gradually refines the layout at each level, improving the final result.
• Adaptive Forces: Some methods adjust the forces depending on the structure of the graph, helping to make the layout process faster and more accurate.
• Graph Simplification: For large graphs, simplifying the graph (e.g., by removing less important edges) can reduce complexity, speeding up the layout process.