Graph Theory - Multigraphs

---

---

Multigraph

A multigraph is a type of graph that allows multiple edges between the same pair of vertices. These multiple edges are also called parallel edges. In a multigraph, an edge can appear more than once between two vertices, representing different connections or relationships.

In a simple graph, we restrict the number of edges between any two vertices to be one, and no loops (edges connecting a vertex to itself) are allowed. In contrast, multigraphs allows multiple edges and loops, which makes them more flexible for modeling complex relationships.

Multigraphs are useful in various applications like transportation networks, communication systems, and complex social networks, where multiple relationships between the same entities can exist simultaneously.

This tutorial will cover different aspects of multigraphs, including their definition, types, properties, and applications.

Example

Consider a graph with vertices V = {A, B, C, D} and edges E = {(A, B), (A, B), (A, D), (A, D), (A, C), (B, D)}. This graph is a multigraph because −

• There are multiple edges between A and B & A and D (parallel edges).
• There are no restrictions on the number of edges between any two vertices.

Representation of Multigraphs

Multigraphs can be represented in various ways, similar to simple graphs. However, since multigraphs may have multiple edges between the same pair of vertices, special attention must be given to their representation.

Adjacency Matrix Representation

The adjacency matrix for a multigraph is a square matrix where each element represents the number of edges between the corresponding vertices. Instead of using just 0 or 1 to denote the presence or absence of an edge, the matrix will contain the number of parallel edges between any two vertices.

Example

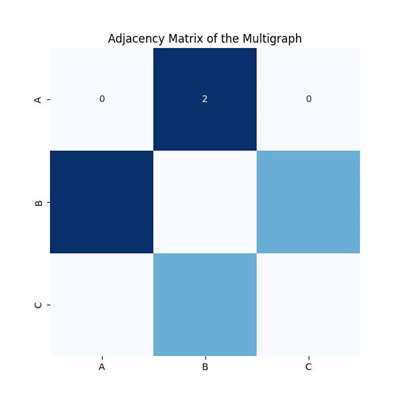
Consider the multigraph with vertices A, B, C and edges E = {(A, B), (A, B), (B, C)}. The adjacency matrix would look like this −

	A	B	C
A	0	2	0
B	2	0	1
C	0	1	0

This matrix indicates that −

• There are 2 edges between A and B.
• There is 1 edge between B and C.
• There are no edges between A and C.

Adjacency List Representation

In the adjacency list representation of a multigraph, each vertex is associated with a list of edges that connect it to other vertices. Instead of just listing each adjacent vertex once, we count the number of times each vertex appears in the list to represent multiple edges.

Example

For the multigraph with vertices A, B, C and edges E = {(A, B), (A, B), (B, C)}, the adjacency list representation would be −

• A: [B, B]
• B: [A, C]
• C: [B]

Degree of a Vertex in Multigraphs

The degree of a vertex in a multigraph is the number of edges incident to it, considering multiple edges as well. If multiple edges exist between two vertices, they are counted as separate edges for degree calculation.

• The degree of a vertex v, denoted deg(v), is the sum of the number of edges incident to v.
• In a multigraph, an edge between two vertices is counted for both vertices.

Types of Degree

The types of degree in a multigraph are similar to those in simple graphs −

• In-degree: The number of edges directed towards a vertex (used in directed multigraphs).
• Out-degree: The number of edges directed away from a vertex (also used in directed multigraphs).

Example

For the multigraph with vertices A, B, C and edges E = {(A, B), (A, B), (B, C)}, the degree of each vertex is:

• deg(A) = 2 (since there are two edges from A to B)
• deg(B) = 3 (two edges from A to B and one edge from B to C)
• deg(C) = 1 (one edge from B to C)

Properties of Multigraphs

Multigraphs have some unique properties due to the presence of multiple edges between vertices. These properties help distinguish multigraphs from simple graphs and provide a better understanding of their structure.

Multiple Edges

In a multigraph, multiple edges (parallel edges) between the same pair of vertices are allowed. This is one of the key differences between multigraphs and simple graphs, where only one edge between any two vertices is allowed.

Loops

In a multigraph, loops (edges that connect a vertex to itself) are also allowed. This is another important distinction from simple graphs, where loops are not allowed.

Maximal Number of Edges

For a multigraph with n vertices, there is no upper bound on the number of edges that can exist between any two vertices, as long as multiple edges and loops are allowed. The total number of edges in the graph depends on the number of parallel edges between vertices.

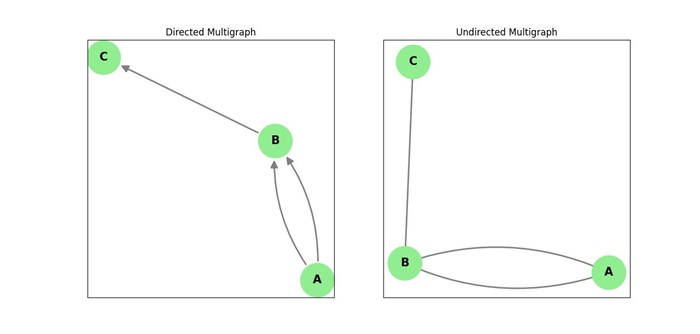
Directed and Undirected Multigraphs

Multigraphs can be either directed or undirected, and this influences the structure of the graph −

• Directed Multigraphs: The edges have a direction, meaning that each edge has a starting and ending vertex.
• Undirected Multigraphs: The edges have no direction, meaning the relationship between the two vertices is symmetric.

Subgraphs in Multigraphs

A subgraph of a multigraph is a graph formed by selecting a subset of vertices and edges from the original graph. A subgraph in a multigraph can include multiple edges between vertices or even loops.

Applications of Multigraphs

Multigraphs are used in various real-life applications where relationships between entities are complex and multiple interactions can exist between the same pair of entities. Here are some key applications −

Transportation Networks

In transportation systems, multiple routes can exist between the same two locations. A multigraph can model these situations, where the vertices represent locations, and the edges represent different routes between locations.

Communication Networks

Communication systems often have multiple communication channels between the same pair of devices. A multigraph can represent these systems by allowing multiple edges between the same pair of devices.

Social Networks

In social networks, individuals can have multiple types of relationships with each other. A multigraph can model these relationships by allowing multiple edges between two individuals, each representing a different type of relationship (e.g., friendship, professional connection, etc.).

Routing and Optimization Problems

Multigraphs are used to model problems like packet routing in networks, where multiple routes between nodes are available. The multiple edges represent different paths or communication links between nodes, making it easier to find the optimal path.