Graph Theory - Graph Embedding

---

---

Graph Embedding

Graph embedding is the process of mapping the vertices and edges of a graph into a specific space (such as a vector space) while preserving its structural properties. This mapping can be done in various dimensions, such as 2D, 3D, or higher-dimensional spaces, depending on the application.

The goal of embedding is to represent the graph in a way that preserves its connectivity and adjacency relationships. This process involves arranging the graph's vertices and edges in space while optimizing specific properties, such as minimizing edge lengths or achieving desired spatial arrangements.

Types of Graph Embedding

There are various methods for embedding graphs, depending on the goals and the structure of the graph. The two main categories of graph embedding are −

• Graph Drawing Embedding: In this type, the goal is to represent the graph visually in a 2D or 3D space while maintaining its connectivity and structure. This is useful in visualization tasks where edge crossings need to be minimized, and the graph needs to be readable.
• Graph Representation Learning: Here, the goal is to represent the graph as a low-dimensional vector space that retains its key features. These embeddings are commonly used in machine learning applications, where graphs are used as input data to algorithms.

Graph Drawing Embedding

Graph drawing embedding refers to positioning the vertices of a graph in a geometric space such that their relationships and connectivity are preserved, and the graph is visually refined (i.e., edge crossings are minimized, and the graph is easy to read). Popular algorithms for graph drawing embedding are −

• Force-directed algorithms: These algorithms use physical forces (like electrical or spring forces) between vertices to minimize edge crossings and evenly distribute the nodes in the graph. The most common example is the Fruchterman-Reingold algorithm.
• Spectral embedding: This method uses the eigenvalues and eigenvectors of the graph's Laplacian matrix to position the nodes in a space that reflects the graph's structural properties.
• Planar embedding: In this case, the graph is embedded into a 2D plane such that no edges cross. This is particularly useful for planar graphs.

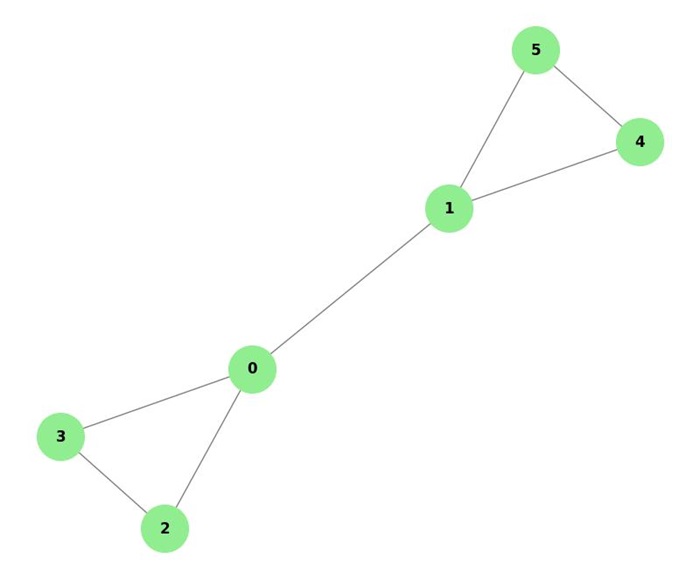
Example: Force-directed Graph Drawing

Consider a graph with 6 vertices and 7 edges. By applying a force-directed algorithm, we simulate attractive forces between connected nodes and repulsive forces between all pairs of nodes.

This results in a layout where the nodes are evenly distributed, and edge crossings are minimized, creating a clear graph representation −

Graph Representation Learning

Graph representation learning converts a graph into a vector space, where each node, edge, or subgraph is represented as a fixed-size vector.

These vectors capture both the structural and semantic properties of the graph, making them useful for various machine learning tasks such as node classification, link prediction, and graph classification. There are two main approaches to graph representation learning −

• Node Embedding: In node embedding, each node is represented as a vector in a low-dimensional space. Methods like DeepWalk, node2vec, and LINE are popular algorithms for node embedding.
• Graph Embedding: Graph embedding involves learning a representation for the entire graph. Methods such as graph2vec are used to embed entire graphs into vector spaces, which can be used for graph classification tasks.

Algorithms for Graph Embedding

There are various commonly used algorithms for graph embedding in machine learning tasks. These algorithms focus on learning low-dimensional representations of nodes and graphs. Some of the most popular algorithms are −

• DeepWalk: DeepWalk is a node embedding algorithm that learns embeddings based on random walks on the graph. It treats the random walks as sentences and uses the Skip-gram model (from natural language processing) to learn node embeddings.
• node2vec: This is an extension of DeepWalk that introduces biased random walks. It allows the user to control the trade-off between breadth-first search (BFS) and depth-first search (DFS), which helps in capturing both local and global structures of the graph.
• LINE: LINE (Large-scale Information Network Embedding) is another popular algorithm for node embedding. It focuses on preserving both the first-order and second-order proximities of nodes in the graph, making it suitable for large-scale networks.
• graph2vec: Unlike node embedding, graph2vec is used to embed entire graphs into a fixed-size vector. It uses subgraph isomorphisms and graph kernels to capture the structural features of the entire graph.

Example: DeepWalk Embedding

Consider a graph with 10 nodes and 15 edges. Using the DeepWalk algorithm, we can generate random walks starting from each node. These random walks are then treated as sentences and fed into a Skip-gram model to learn embeddings for each node in the graph.

The resulting vector representations capture both the local and global structure of the graph −

In the above image, the first graph displays the original graph layout with nodes positioned based on network structure.

The second graph visualizes random 2D embeddings for each node, simulating a simplified DeepWalk approach. These embeddings do not reflect the actual graph structure but show nodes in a 2D space based on random values.

Graph Convolutional Networks (GCN)

Graph Convolutional Networks (GCNs) are deep learning-based models for graph embedding. Unlike Node2Vec and DeepWalk, which rely on random walks, GCNs uses graph convolutional layers to learn node representations through a series of transformations. These transformations aggregate information from neighboring nodes in the graph to generate embeddings.

GCNs are particularly powerful because they can capture both local and global graph structures and can be trained end-to-end using gradient-based optimization methods. They are widely used in graph-based machine learning tasks such as node classification, link prediction, and graph classification.

Graph Embedding for Link Prediction

Link prediction is a common problem in graph theory, where the goal is to predict missing edges between nodes in a graph. Graph embedding plays an important role in link prediction tasks by providing a low-dimensional representation of nodes and their relationships.

In link prediction, the idea is that the closer two nodes are in the embedding space, the more likely it is that there is an edge between them in the original graph. This can be achieved by computing the similarity between node embeddings and using it to predict potential links.

For example, the cosine similarity between two node embeddings can be used as a measure of their likelihood of being connected in the original graph.

Applications of Graph Embedding

Graph embedding has various applications across different domains, such as −

• Social Network Analysis: Graph embedding is used to analyze social networks, where users are represented as nodes, and relationships between users are represented as edges. Node embeddings can be used for tasks like community detection, recommendation, and link prediction.
• Biological Networks: In biological networks (such as protein-protein interaction networks), graph embedding can help in identifying important biological relationships and predicting potential drug-target interactions.
• Recommender Systems: Graph embedding is used in recommender systems to learn low-dimensional representations of users and items in collaborative filtering models. These embeddings help improve recommendation accuracy.
• Computer Vision: In computer vision, graph embedding is used to analyze and represent relationships between different parts of an image or video, enabling tasks such as object recognition and scene segmentation.

Challenges in Graph Embedding

While graph embedding techniques are highly effective in various applications, they come with several challenges as well −

• Scalability: Many graph embedding algorithms, especially those that rely on random walks (e.g., Node2Vec, DeepWalk), can struggle to scale for very large graphs with millions of nodes and edges.
• Capturing Graph Structure: Ensuring that the embedding accurately retains the graph's structure and properties (such as node connectivity, community structure, and edge relationships) is challenging, especially for complex graphs.
• Overfitting: When training graph embedding models, there is a risk of overfitting to the training data, especially if the graph is sparse or contains noisy information.