Graph Theory - Trees

Quiz

Trees in Graph Theory

A tree is a special type of graph that is connected and acyclic, meaning it has no cycles or loops. It consists of nodes (vertices) and edges (connections between nodes), where there is exactly one path between any two nodes.

In other words, a tree is a graph where, for any two nodes, you can traverse from one to the other without retracing any edge, and there are no circular paths.

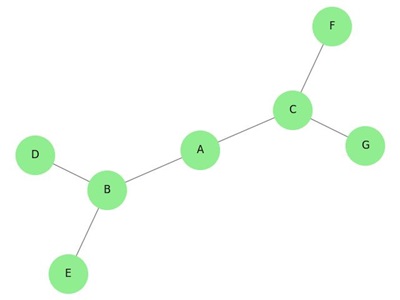
Properties of Trees

A tree has several defining properties, which are important in understanding its behavior and characteristics. These include the following −

Connectivity

A tree is a connected graph, meaning there is a path between any two vertices. Unlike general graphs, trees have no isolated vertices.

Acyclic Nature

A tree is acyclic, meaning it does not contain any cycles. This is one of the defining characteristics of a tree, distinguishing it from general graphs.

Number of Edges

For a tree with n vertices, there are always n-1 edges. This is a fundamental property of trees and is used in algorithms involving trees.

Leaf Nodes

A leaf in a tree is a vertex that has only one edge connected to it (also known as a terminal vertex). A tree can have one or more leaf nodes.

Rooted Trees

A tree can be considered as a rooted tree if one vertex is designated as the "root," and all edges have a direction pointing away from this root. In a rooted tree, the hierarchy is clearly defined, and each vertex has a parent and potentially multiple children.

Subtrees

Any tree can be divided into smaller trees by removing edges. A subtree is a part of a tree that is itself a tree, consisting of a vertex and all its descendants.

Depth of a Tree

The depth of a tree is the length of the longest path from the root to any leaf. The depth of a tree gives insight into its hierarchy and is important for various tree-based algorithms.

Height of a Tree

The height of a tree is the number of edges on the longest path from the root to any leaf. The height is a measure of the longest possible chain of nodes in the tree.

Level of a Node

The level of a node is defined by its distance from the root. The root is at level 0, its direct children are at level 1, and so on.

Balanced Trees

A tree is said to be balanced if the height difference between the left and right subtrees of any node is minimal (usually no greater than 1). Balanced trees are important for performance optimization in search operations.

Height Balanced and Weight Balanced Trees

Height-balanced trees are those where the difference in heights of subtrees of any node is bounded by a constant (commonly 1). Weight-balanced trees ensure that the number of nodes in the left and right subtrees of any node is approximately equal.

Forest

A forest is a disjoint collection of trees. If you remove any edge from a tree, the graph becomes a forest. Each connected component in a forest is a tree.

Types of Trees

Trees come in various types, each with a different purpose or solving a specific problem. These include −

Binary Tree

A binary tree is a tree where each node has at most two children. Binary trees are widely used in computer science for tasks like searching, sorting, and hierarchical data storage.

Each node can have a left and a right child.
Binary trees are used in implementing binary search trees, heaps, and expression trees.

Binary Search Tree (BST)

A binary search tree is a binary tree in which each node follows the property that all the values in the left subtree are less than the node's value, and all the values in the right subtree are greater than the node's value. This structure allows for search, insertion, and deletion operations.

AVL Tree

An AVL tree is a self-balancing binary search tree. In an AVL tree, the difference in height between the left and right subtrees of any node is at most 1. This balancing property ensures that operations like search, insertion, and deletion are efficient (O(log n) time complexity).

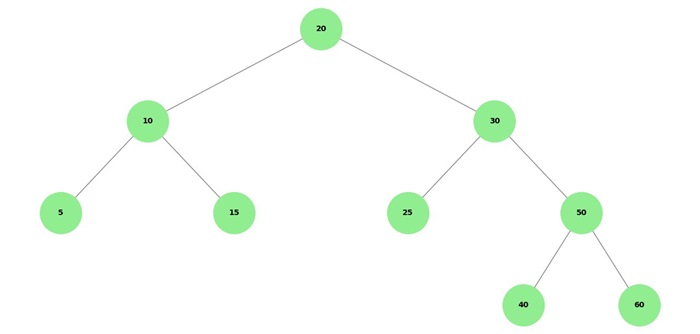
Red-Black Tree

A Red-Black Tree is a type of self-balancing binary search tree, where each node contains an extra bit for determining its coloreither red or black. The tree maintains several properties that help it remain balanced, ensuring that operations such as search, insert, and delete can be performed efficiently in logarithmic time.

Key properties of a Red-Black Tree include:

Node Color: Every node is either red or black.
Root is Black: The root node is always black.
Red Node Property: No two red nodes can be adjacent; red nodes cannot have red children.
Black Height: Every path from a node to its descendant leaves must have the same number of black nodes.
Balanced Tree: The tree is balanced in such a way that the longest path from the root to a leaf is no more than twice as long as the shortest path, maintaining efficient operations.

Inorder Traversal:  [5, 10, 15, 20, 25, 30, 35, 40, 50]

Red-Black Tree Structure:
Root: (20, black)
   L--- (10, black)
      L--- (5, red)
      R--- (15, red)
   R--- (30, black)
      L--- (25, red)
      R--- (40, black)
         L--- (35, red)
         R--- (50, red)

B-tree

A B-tree is a self-balancing tree data structure that is commonly used in databases and file systems to store and manage large amounts of data. It is an ordered, balanced tree where each node can have multiple children and contains multiple keys.

The B-tree is designed to handle read and write operations on large blocks of data, making it well-suited for systems where data is stored on disk.

Key characteristics of a B-tree are −

Balanced: All leaf nodes are at the same level, ensuring that the tree remains balanced and operations like search, insertion, and deletion can be performed efficiently in logarithmic time.
Nodes with Multiple Keys: Unlike binary trees, each node in a B-tree can have multiple keys and multiple children. This allows for more efficient storage and reduces the number of disk accesses required for searching.
Efficient Disk Access: B-trees are designed to minimize the number of disk reads or writes, which is important for systems that manage large datasets that cannot fit entirely into memory.

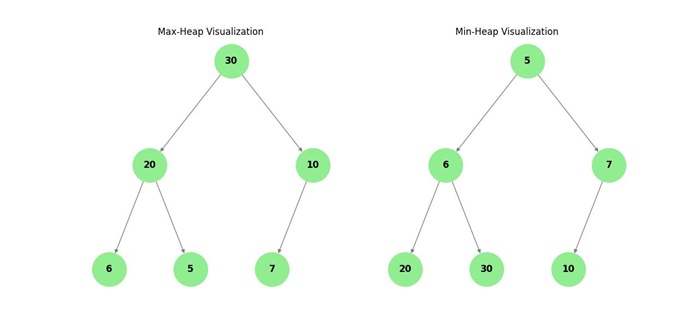
Heap

A heap is a specialized tree-based data structure that satisfies the heap property. It is a complete binary tree, meaning all levels of the tree are fully filled except possibly for the last level, which is filled from left to right. The heap is commonly used in algorithms like heap sort and in data structures like priority queues.

There are two main types of heaps −

Max-Heap: In a max-heap, the key of each parent node is greater than or equal to the keys of its children. This ensures that the maximum key is at the root of the tree.
Min-Heap: In a min-heap, the key of each parent node is less than or equal to the keys of its children. This ensures that the minimum key is at the root of the tree.

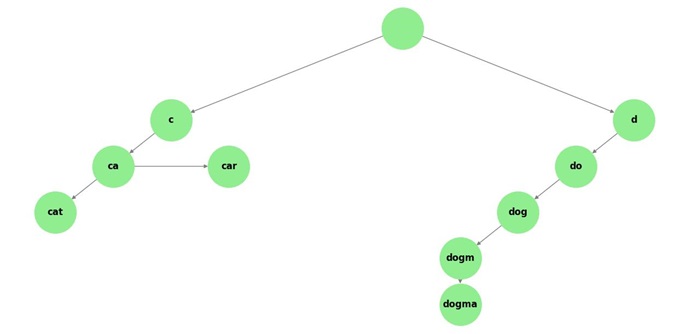
Trie

A Trie (or prefix tree) is a specialized tree-like data structure used for storing and retrieving keys, often strings. It is mainly used for tasks like autocomplete, spell checking, and IP routing. Each node in a trie represents a single character of the key, and the path from the root to a node forms a prefix of the key.

Key characteristics of a Trie are −

Prefix Tree: Tries are often referred to as "prefix trees" because they store common prefixes of strings together, allowing for fast retrieval of words that share prefixes.
Nodes Represent Characters: Each node in the trie corresponds to a single character of the key, and the edges between nodes represent the transitions between characters in the keys.
Efficient Search: Tries provide search, insert, and delete operations, which are often faster than other data structures like hash tables, especially for string-related operations.

Segment Tree

A segment tree is a binary tree used for storing intervals or segments. It is useful in problems where intervals need to be queried or updated efficiently, such as in range query problems.

It is a data structure used for answering range queries and updating elements in an array or list. It is particularly useful when you need to perform operations like sum, minimum, maximum, greatest common divisor (GCD), or other associative operations on intervals or ranges of elements.

Key characteristics of a Segment Tree are −

Range Queries: Segment Trees allow querying the result of an operation (like sum or minimum) on a specific range of elements in O(log n) time, where n is the size of the array.
Efficient Updates: Segment Trees allow you to update an element in the array and reflect that change in the tree, again in O(log n) time.
Binary Tree Structure: A Segment Tree is typically represented as a binary tree, where each node represents a segment or subrange of the array. The leaves of the tree represent individual elements of the array.

Query min in range [1, 4]: 3
Query min in range [1, 4] after update: 3

Fenwick Tree

A Fenwick Tree, also known as a Binary Indexed Tree (BIT), is a data structure used to perform prefix sum queries and updates on an array. It is a binary tree-like structure that allows for fast cumulative frequency table calculations, with both updates and queries being performed in O(log n) time.

Key characteristics of a Fenwick Tree are −

Prefix Sum Queries: The primary operation of a Fenwick Tree is to quickly calculate the sum of elements from the beginning of the array up to a given index.
Efficient Updates: Fenwick Trees allow updates to individual elements of the array in O(log n) time, ensuring that changes are reflected quickly in subsequent queries.
Space-Efficient: The Fenwick Tree uses an array of the same size as the input array, making it a space-efficient alternative to other data structures like Segment Trees.

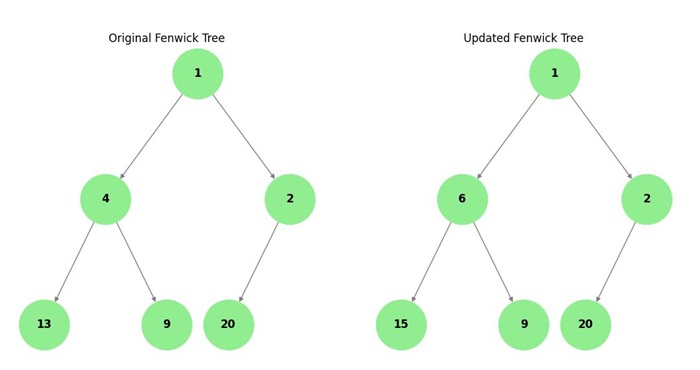
Query sum in range [1, 4]: 13
Query sum in range [1, 4] after update: 15

Decision Tree

A decision tree is used in machine learning to represent decisions and their possible consequences, including outcomes, costs, and utility. Decision trees are commonly used in classification and regression tasks.

It is a tree-like structure where each internal node represents a decision based on a feature, each branch represents an outcome of the decision, and each leaf node represents a class label (in classification) or a continuous value (in regression).

Key characteristics of a Decision Tree are −

Root Node: The topmost node in the tree, which represents the entire dataset and the first decision point based on a feature.
Internal Nodes: Each internal node represents a decision or test based on a feature, splitting the dataset into subsets based on certain conditions.
Leaf Nodes: The terminal nodes of the tree, which represent the output of the decision processeither a class label (in classification tasks) or a predicted value (in regression tasks).

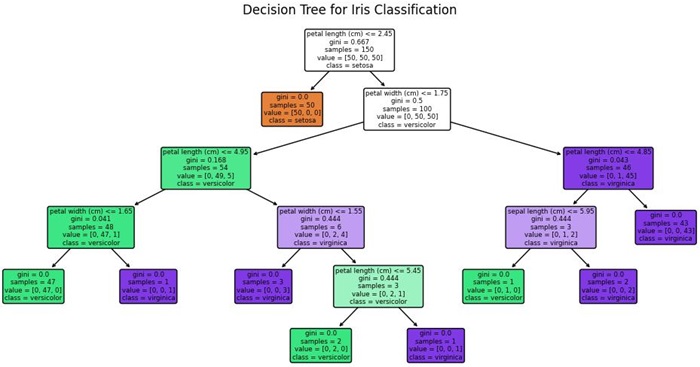
Applications of Trees

Trees are used in various applications across different fields. Some of the notable applications are −

Data Structures: Trees are the foundation of many data structures, such as heaps, binary search trees, AVL trees, and tries, used for efficient searching, insertion, and deletion operations.
Computer Networks: Trees are used in network routing algorithms, like the spanning tree protocol, which helps in creating efficient routing paths for data transmission in computer networks.
File Systems: Many modern file systems use tree structures to store directories and files in a hierarchical manner, which enables efficient file retrieval and management.
Expression Parsing: Expression trees, a type of binary tree, are used to represent arithmetic expressions. These trees allow easy evaluation and optimization of expressions in compilers and calculators.
Decision Making: Decision trees are used in machine learning for classification and regression tasks. They help in decision-making by recursively splitting data into subsets based on feature values.
Database Indexing: Database indexing often uses B-trees and B+-trees to allow efficient querying of large datasets. These trees allow logarithmic time complexity for searching, inserting, and deleting records in a database.

Tree Traversals

Traversing a tree involves visiting all the nodes in a specific order. There are several standard ways to traverse a tree −

Pre-order Traversal: In a pre-order traversal, the root node is visited first, followed by the left subtree, and then the right subtree.
In-order Traversal: In an in-order traversal, the left subtree is visited first, followed by the root node, and then the right subtree. This is particularly useful in binary search trees as it returns values in sorted order.
Post-order Traversal: In a post-order traversal, the left subtree is visited first, followed by the right subtree, and then the root node. This traversal is useful in situations like deleting nodes from a tree.
Level-order Traversal: In a level-order traversal, all the nodes at each level are visited from top to bottom, starting from the root. This can be implemented using a queue data structure.

Print Page