Graph Theory - Applications

---

---

Applications of Graph Theory

Graph theory is widely used in numerous fields, ranging from computer science to biology, social networks, and more. Its ability to model relationships, structures, and processes has made it an important tool in solving real-world problems. This chapter explores some of the key applications of graph theory.

Social Networks

One of the most common applications of graph theory is in the analysis of social networks. In this context, vertices represent individuals or entities, and edges represent relationships or interactions between them.

Social network analysis is used to understand patterns of communication, influence, and collaboration within groups.

Example: Social Network Analysis

Consider a social network where individuals are connected based on mutual friendships. Graph theory can be used to identify central individuals (centrality), detect communities, and understand the overall network structure −

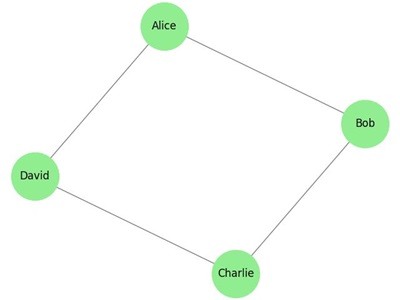
This image shows a simple social network where individuals are connected by friendships or interactions.

Computer Networks

Graph theory is important in the design, analysis, and optimization of computer networks, such as the internet and local area networks (LANs). Nodes represent devices (e.g., computers, routers), and edges represent communication links.

Graph algorithms like shortest path, minimum spanning tree, and flow algorithms are used to ensure efficient data transmission, minimize network congestion, and optimize resource allocation.

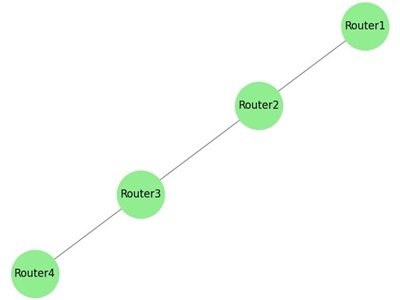
Example: Computer Network Topology

The following example image shows a simple computer network topology where devices are connected via communication links −

Routing and Navigation

Graph theory plays an important role in routing algorithms, such as those used in GPS navigation systems and internet routing protocols. In routing problems, locations are represented as vertices, and paths between locations are edges.

Algorithms like Dijkstra's algorithm help find the shortest path between two vertices, optimizing travel time and costs.

Example: Shortest Path in Routing

The following example image displays the shortest path between two vertices in a weighted graph −

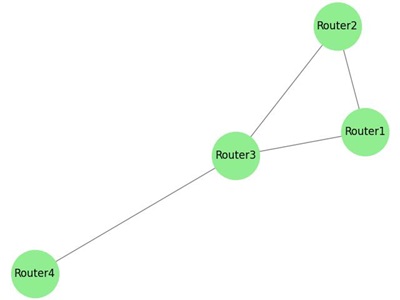
Shortest path: ['Router1', 'Router3', 'Router4']
Shortest distance: 10

Transportation and Logistics

Graph theory is fundamental in the modeling and optimization of transportation systems, such as road networks, railway networks, and air traffic control.

Cities and transport hubs are represented as vertices, and transportation routes (e.g., roads, tracks, or air routes) are represented as edges.

Graph theory helps in optimizing the shortest path for delivery, minimizing transportation costs, and planning the most efficient routes.

Example: Route Optimization

The following image shows the use of graph theory in representing an airport flight network, where airports are connected by direct flights −

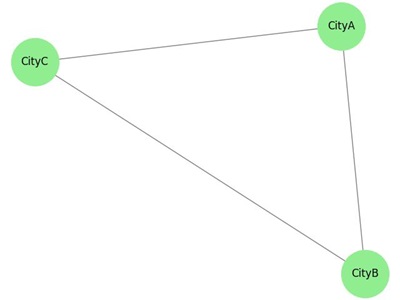
Shortest path: ['CityA', 'CityB', 'CityC']

Biological Networks

Graph theory is extensively used in biology to model complex networks such as protein-protein interaction networks, gene regulatory networks, and ecological networks. In these biological networks, vertices represent biological entities (e.g., genes, proteins, species), and edges represent interactions or relationships between them.

Analyzing these networks helps in understanding biological processes and identifying potential targets for drug discovery.

Example: Protein-Protein Interaction Network

The following image shows a simplified representation of a protein-protein interaction network, where proteins are connected if they interact with each other −

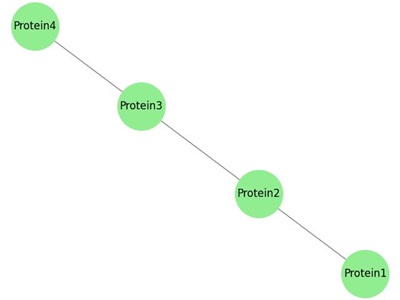
Recommendation Systems

Graph theory is widely used in recommendation systems, such as those found in online platforms like Amazon, Netflix, and YouTube. Recommendation systems use graph theory to suggest items to users based on their preferences.

In these systems, users and products (or movies, videos, etc.) are represented as vertices, and the relationships between them (e.g., user ratings or views) are represented as edges.

Graph-based algorithms are used to recommend new items based on user behavior or similarities between users.

Example: Collaborative Filtering

The following image illustrates the concept of collaborative filtering in recommendation systems using graph theory, where similar users are connected based on shared preferences −

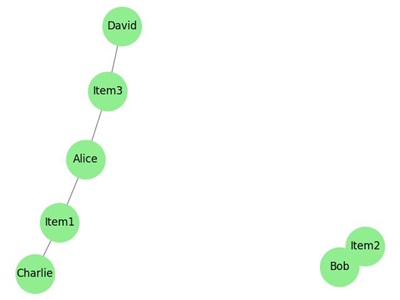
In this bipartite graph:

Alice and Charlie share a common preference for Item1.
Alice and David share a common preference for Item3.