Graph Theory - Simple Graphs

---

---

Simple Graph

A simple graph is a graph that does not have multiple edges (also called parallel edges) between two nodes and does not contain loops (edges that connect a node to itself).

In a simple graph, the edges are undirected, meaning there is no specific direction associated with them. If an edge connects vertex A to vertex B, the edge can be traversed in both directions. The vertices in a simple graph are typically represented as nodes, and the edges represent the connections between them.

Simple graphs are widely used in various applications such as network design, social networks, and scheduling problems, where relationships between entities are symmetric (i.e., there is no need for directionality or multiple connections between the same pair of entities).

We will discuss all aspects of simple graphs, from their definitions to the different types, properties, and applications in this tutorial.

Example

Consider a graph with nodes V = {A, B, C, D} and edges E = {(A, B), (A, C), (B, D)}. This is a simple graph because −

• There are no loops.
• There is only one edge between any two nodes (no multiple edges).

Representation of Simple Graphs

A simple graph can be represented in multiple ways, allowing us to store and manipulate the graph. The most common methods include the adjacency matrix and the adjacency list, each with its own advantages depending on the operations we need to perform.

Adjacency Matrix Representation

One of the most common ways to represent a simple graph is through an adjacency matrix. An adjacency matrix is a square matrix where each element represents whether a pair of vertices is connected by an edge.

If there is an edge between vertex i and vertex j, then the matrix element A[i][j] = 1, otherwise, A[i][j] = 0.

Example

For a simple graph with vertices A, B, C, the adjacency matrix would look like this −

	A	B	C
A	0	1	1
B	1	0	1
C	1	1	0

This matrix shows that −

• A is connected to B and C.
• B is connected to A and C.
• C is connected to A and B.

Adjacency List Representation

Another common representation is the adjacency list. In this format, each vertex is associated with a list of its adjacent vertices. In this representation, the graph is stored as an array or a collection of lists, where each list contains the vertices that are directly connected to the vertex it represents.

In an undirected graph, if there is an edge between vertex A and vertex B, both A's list and B's list will contain each other. In a directed graph, however, an edge from A to B will only appear in A's list, not B's.

Example

For the same simple graph with vertices A, B, C, the adjacency list would look like this−

• A: [B, C]
• B: [A, C]
• C: [A, B]

Degree of a Vertex

The degree of a vertex in a graph is the number of edges incident to it. In a simple graph, this is simply the number of edges that are connected to that vertex.

• The degree of a vertex v, denoted deg(v), is the number of edges connected to v.
• In a simple graph, each edge contributes one to the degree of each of its two endpoints.

Types of Degree

Following are the two different types of degrees in a graph −

• In-degree: The number of edges directed toward a vertex (used in directed graphs, not applicable in simple undirected graphs).
• Out-degree: The number of edges directed away from a vertex (also for directed graphs).

Example

For the graph with vertices A, B, C −

• deg(A) = 2
• deg(B) = 2
• deg(C) = 2

Each vertex is connected by 2 edges.

Properties of Simple Graphs

Simple graphs have several important properties that help in understanding their structure and behavior. These properties include concepts like the number of vertices, edges, degree of vertices, and whether the graph is connected or disconnected.

Number of Edges in a Simple Graph

The number of edges in a simple graph is constrained by the number of vertices. In a graph with n vertices, the maximum possible number of edges is n(n-1)/2, which occurs when every pair of distinct vertices is connected by a unique edge.

Example

For a simple graph with 4 vertices, the maximum number of edges is −

4(4-1)/2 = 6

Complete Graph

A complete graph is a simple graph where every pair of distinct vertices is connected by a unique edge. The complete graph with n vertices is denoted as K_n.

Example

For n = 5, the complete graph K_5 would have 5 vertices and 5 edges, with every vertex connected to every other vertex.

Null Graph

A null graph is a simple graph with no edges. It only contains vertices, and no two vertices are connected. In other words, the graph is completely disconnected.

Here are the key points about a null graph −

• No Edges: A null graph contains no edges, meaning there are no connections between any of its vertices.
• Any Number of Vertices: A null graph can have any number of vertices, but it will always have zero edges, regardless of the number of vertices.
• Disconnected: Since there are no edges, all vertices in a null graph are isolated and disconnected from each other.

Isolated Vertex

An isolated vertex is a vertex in a graph that has no edges connected to it. In other words, it is a vertex that does not share a direct connection (edge) with any other vertex in the graph.

In both undirected and directed graphs, an isolated vertex does not participate in any relationships or interactions with other vertices. It exists as a standalone node, with no adjacent vertices.

In this image, D is the isolated vertex.

Connected Graph

A connected graph is a graph in which there is a path between every pair of vertices. In other words, you can travel from any vertex to any other vertex by following the edges of the graph.

All vertices in a connected graph are part of a single connected component, meaning there are no isolated groups of vertices. A connected graph can be either directed or undirected, but in both cases, all vertices are reachable from one another.

Disconnected Graph

On the other hand, a disconnected graph is a graph where at least two vertices do not have a path between them.

This means the graph consists of two or more disconnected components, where each component is a subgraph in which all vertices are connected, but there is no connection between the components.

In a disconnected graph, some vertices or groups of vertices are isolated from others, making it impossible to travel between all pairs of vertices.

Subgraph

A subgraph is a portion of a graph that consists of a subset of the original graph's vertices and edges. It is formed by selecting some vertices and the edges that connect them from the original graph. A subgraph can be a smaller graph that still maintains the connections and relationships present in the original graph.

A subgraph can be classified as an induced subgraph or a general subgraph −

• An induced subgraph includes all the edges between the selected vertices that are present in the original graph.
• A general subgraph may not include all such edges, only a subset of them.

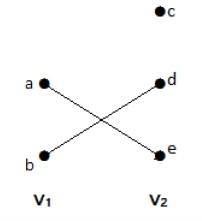
Bipartite Graph

A bipartite graph is a simple graph where the vertex set can be divided into two disjoint sets such that no two vertices within the same set are adjacent.

Types of Simple Graphs

Simple graphs can be classified into different types based on their structure and characteristics. These types include undirected, directed, weighted, and unweighted graphs, each with its own specific features and use cases.

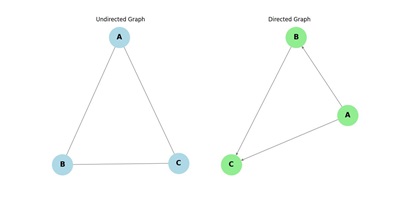
Directed vs. Undirected Graphs

The directed and undirected graphs are defined below −

• In an undirected graph, the edges have no direction, meaning the relationship is mutual.
• In a directed graph (or digraph), each edge has a direction, meaning the relationship is one-way.

Weighted Graph

A weighted graph is a graph in which each edge has a weight or cost associated with it. In a simple graph, the weights could represent distances, time, or other quantities depending on the application.

In this image, the edges are labeled with weight.

Applications of Simple Graphs

Simple graphs are used in various real-life applications such as network modeling, social media analysis, and computer networks. They help in representing relationships and connections between entities, making it easier to solve problems like routing, connectivity, and resource allocation.

Social Networks

Simple graphs are widely used to model social networks where nodes represent individuals and edges represent relationships or connections between them.

Transportation Networks

Simple graphs can represent transportation systems, where the vertices represent locations and the edges represent routes connecting those locations.

Computer Networks

Simple graphs are also used to represent computer networks, with nodes representing computers and edges representing communication links between them.

Scheduling and Resource Allocation

In scheduling problems, simple graphs can model tasks and the dependencies between them, where edges represent the precedence constraints between tasks.