Graph Theory - Treewidth

Quiz

Treewidth

Treewidth in graph theory measures how close a graph is to being a tree. It is a numerical value assigned to a graph that represents its complexity in terms of tree-like structures −

A tree has a treewidth of 1 because you can represent it with bags containing only two vertices (one vertex plus its neighbor).
A graph with many cycles or a dense structure has a higher treewidth.

The treewidth of a graph G is the minimum width among all tree decompositions of G. A tree decomposition is a way of representing a graph as a tree, where −

Each node of the tree corresponds to a subset of the vertices of the graph, called a "bag."
For each edge in the graph, there must be at least one bag in the tree containing both endpoints of the edge.
If a vertex appears in multiple bags, all those bags must form a connected subtree.

The width of a tree decomposition is the size of the largest bag minus one. The treewidth of the graph is the minimum width over all possible tree decompositions.

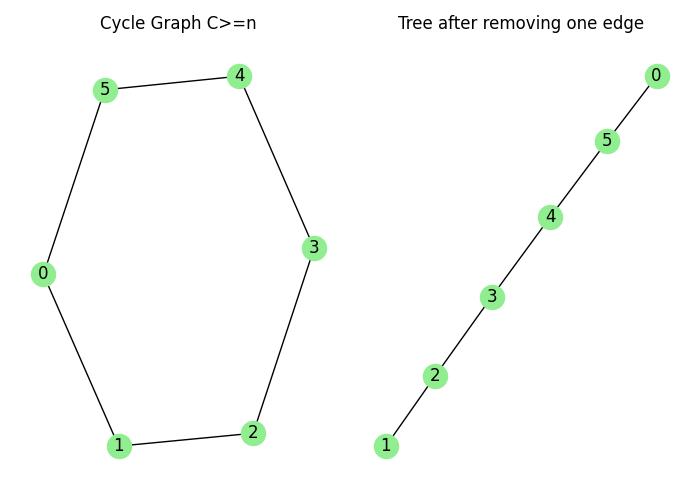
For example, consider a cycle graph C_n with n ≥ 4 −

If you remove one edge from the cycle, it becomes a tree, so the treewidth is 1.
For the original cycle graph, the treewidth is 2, because every tree decomposition will need at least 3 vertices in some bag to include all edges.

Importance of Treewidth

Treewidth plays an important role in graph algorithms and helps solve problems more efficiently. Following are its major uses −

Better Algorithm: Many hard problems become easier to solve on graphs with small treewidth.
Graph Approximation: Treewidth helps in approximating solutions for problems in real-world networks and systems.
Dynamic Programming: Tree decompositions let us use dynamic programming on graphs.
Real-world Applications: It is used in database systems, computer vision, and artificial intelligence to make computations faster.

Tree Decompositions and Treewidth

The concept of treewidth is closely realted to tree decomposition, which represents a graph as a tree-like structure. The treewidth of a graph is defined as one less than the size of the largest set of nodes in a tree decomposition.

A tree decomposition of a graph satisfies the following −

Each node of the graph must be part of at least one "bag" in the tree decomposition.
If two nodes are connected by an edge, there must be at least one "bag" containing both nodes.
The nodes present in a bag must form a connected subtree of the decomposition.

Example of Treewidth Calculation

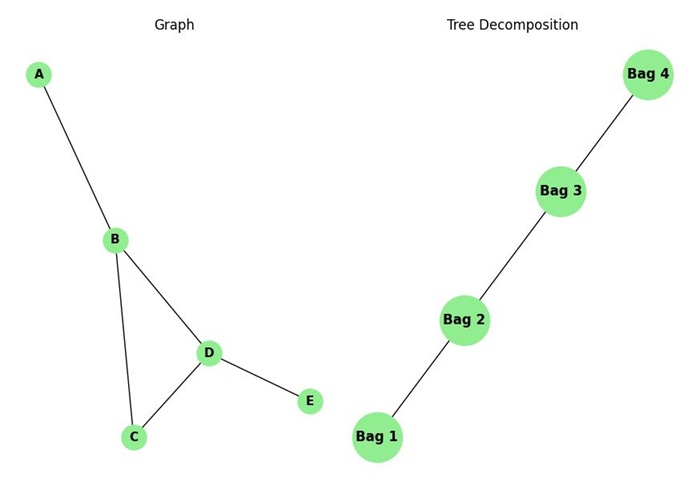
Consider the following graph −

Graph:
Nodes = [A, B, C, D, E]
Edges = [(A, B), (B, C), (C, D), (B, D), (D, E)]

A tree decomposition of this graph looks like this −

Tree Decomposition:
Bag 1: [A, B]
Bag 2: [B, C]
Bag 3: [B, D]
Bag 4: [D, E]

The size of the largest bag is 3, so the treewidth is −

Treewidth = 3 - 1 = 2

Properties of Treewidth

Graphs with small treewidth have the following properties −

Tree-like Structure: Graphs with low treewidth look similar to trees.
Efficient Algorithms: Many graph algorithms work quickly on graphs with low treewidth.
Decomposition Quality: A graph can have multiple tree decompositions, and the treewidth depends on the best decomposition.

Graphs with Bounded Treewidth

Some graph classes have bounded treewidth as follows −

Trees: A tree has a treewidth of 1.
Cycles: A cycle graph with n nodes has a treewidth of 2.
Planar Graphs: Planar graphs can have higher treewidth, but many subclasses have bounded treewidth.

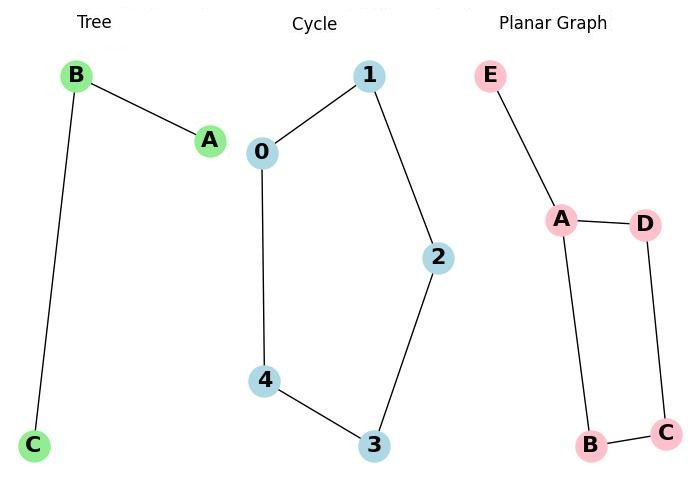
Treewidth Calculation for the Tree

The tree has only 3 nodes (A, B, C), with edges (A, B) and (B, C).
The decomposition has bags like [A, B], [B, C].
The largest bag has size 2, and the treewidth is 2 - 1 = 1.

Treewidth Calculation for the Cycle

The cycle graph here has 5 nodes. We can decompose it into bags like [0, 1], [1, 2], [2, 3], [3, 4], and [4, 0].
Each bag contains 2 nodes that overlap with adjacent bags, ensuring a proper decomposition.
The largest bag has size 2, so the treewidth is 2 - 1 = 2.

Treewidth Calculation for the Planar Graph

The planar graph here has 5 nodes and 5 edges, forming a simple structure.
A tree decomposition might look like [A, B], [B, C], [C, D], [D, A], [A, E], with a treewidth greater than 2 due to the complexity of the graph's structure.
The treewidth here is calculated by finding the size of the largest bag and subtracting 1. The largest bag in this decomposition has size 3 (for example, [A, B, C]), so the treewidth is 3 - 1 = 2.

Treewidth and Computational Problems

Treewidth is useful in solving difficult computational problems. The following list shows some tough problems that are easier to solve on graphs with small treewidth −

Graph Coloring: It becomes easier to find solutions on graphs with low treewidth.
Shortest Path: Tree decompositions allow faster ways to find the shortest path.
Hamiltonian Path: This problem can be solved in less time for graphs with small treewidth.

Example: Algorithm using Treewidth

Let us compute the shortest path using tree decompositions −

# Graph
Nodes = ["A", "B", "C", "D", "E"]
Edges = [("A", "B"), ("B", "C"), ("C", "D"), ("D", "E")]

# Tree Decomposition
Tree_Decomposition = {
    1: ["A", "B"],
    2: ["B", "C"],
    3: ["C", "D"],
    4: ["D", "E"]
}

Now, let us create a simple dynamic programming algorithm to compute the shortest path on this graph using the tree decomposition. We will use the decomposition to break the problem down into subproblems and compute the shortest path for each node in each bag −

# Initialize a dictionary to store shortest path values
Shortest_Path = {}

# Iterate through each bag in the tree decomposition
for bag in Tree_Decomposition.values():
   # For each node in the current bag, compute the shortest path
   for node in bag:
      # Update the shortest path for the node, considering all possible previous nodes
      Shortest_Path[node] = min(Shortest_Path.get(node, float("inf")), ...)
        
# Output the computed shortest path for each node
print(Shortest_Path)

Print Page