Graph Theory - Chromatic Number

---

---

Chromatic Number

The chromatic number of a graph represents the minimum number of colors required to color the vertices of the graph such that no two adjacent vertices share the same color.

The chromatic number helps in understanding the complexity of a graph and is used to analyze the coloring properties of various types of graphs.

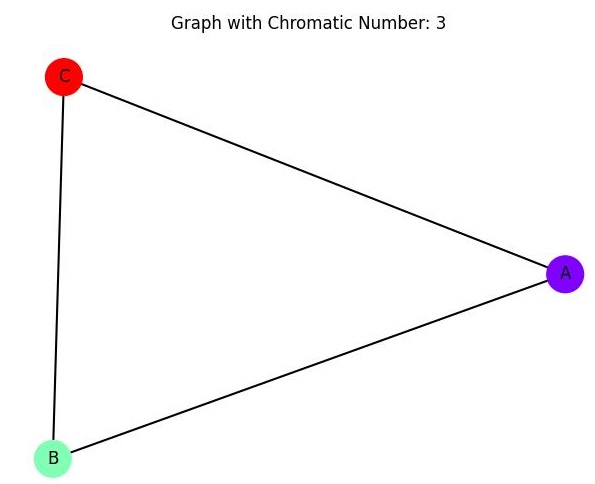
In the above graph, the chromatic number is 3.

A graph is said to be k-colorable if there exists a coloring of the graph using no more than k colors. The chromatic number of the graph is the smallest such value of k.

Chromatic Number and Graph Coloring

The problem of determining the chromatic number of a graph is closely related to the general concept of graph coloring, where the aim is to assign colors to vertices in a way that no two adjacent vertices share the same color.

The chromatic number can be interpreted as the minimal number of "groups" or "categories" needed to partition the vertices such that adjacent vertices do not belong to the same group.

Properties of the Chromatic Number

The chromatic number of a graph have several important properties that are useful in understanding the graph's structure and behavior −

• Upper Bound: The chromatic number is always less than or equal to the number of vertices in the graph. In the worst case, each vertex could be assigned a unique color, resulting in a chromatic number equal to the number of vertices.
• Planar Graphs: By the four-color theorem, any planar graph has a chromatic number of at most 4. This means that a graph that can be drawn on a plane without edge crossings can always be colored with no more than 4 colors.
• Complete Graphs: A complete graph with n vertices has a chromatic number of n, as each vertex must be assigned a unique color to avoid adjacent vertices having the same color.
• Bipartite Graphs: A bipartite graph always has a chromatic number of 2, as it can be colored using two colors, one for each partition of the graph.
• Graph Complement: The chromatic number of a graph is related to the chromatic number of its complement. A lower bound on the chromatic number of a graph is the chromatic number of its complement, and vice versa.

Applications of Chromatic Number

The chromatic number is used in various practical applications, especially where constraints on adjacent elements are important. Some of the important applications are −

• Task Scheduling: In scheduling problems, tasks that share common resources or time slots must not overlap. The chromatic number represents the minimum number of time slots or resources required to schedule all tasks without conflict.
• Register Allocation: In compilers, register allocation is an important optimization process. The chromatic number helps in determining how to assign values to machine registers in a way that minimizes conflicts.
• Map Coloring: The chromatic number is directly related to the problem of coloring maps, where adjacent regions (countries or states) must be assigned different colors. The famous four-color theorem, which states that any map can be colored using at most four colors, is based on this concept.
• Frequency Assignment: In communication networks, frequencies must be assigned to transmitters such that adjacent transmitters do not interfere with each other. The chromatic number helps in determining the minimum number of frequencies required to avoid interference.

Finding the Chromatic Number

Determining the chromatic number of a graph can be a challenging problem, especially for large or complex graphs. There are several approaches and algorithms to help find the chromatic number −

• Greedy Algorithm: The greedy algorithm for graph coloring assigns colors to vertices one by one, ensuring that no two adjacent vertices share the same color. While this algorithm is simple, it does not always produce an optimal coloring and is not guaranteed to find the chromatic number.
• Backtracking: Backtracking is a more thorough method that tries all possible colorings and backtracks whenever it encounters an invalid assignment. While backtracking guarantees an optimal solution, it can be expensive for large graphs.
• Heuristics: Heuristic methods, such as the Welsh-Powell algorithm, try to improve the efficiency of coloring by considering the degree of vertices and attempting to color the most connected vertices first.
• Exact Algorithms: Exact algorithms, such as those based on integer programming, are used to determine the chromatic number for small to medium-sized graphs. While these algorithms can be computationally intensive, they guarantee an optimal solution.

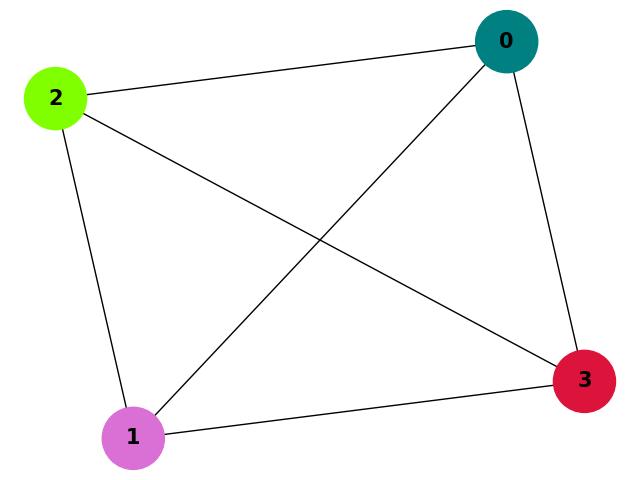
Chromatic Number of a Complete Graph

Consider a complete graph with 4 vertices (K₄). In a complete graph, every pair of vertices is connected by an edge. To color this graph, each vertex must have a unique color, so the chromatic number of K₄ is 4.

A complete graph is a graph in which every pair of distinct vertices is connected by an edge. It is denoted as K_n, where n represents the number of vertices.

Graph:

• Vertices: 0, 1, 2, 3
• Edges: 01, 02, 03, 12, 13, 23

Chromatic Number: 4

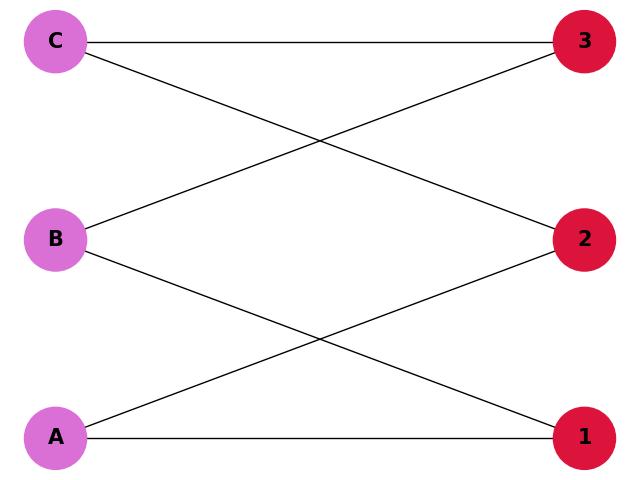
Chromatic Number of a Bipartite Graph

Consider a bipartite graph with two sets of vertices: {A, B, C} and {1, 2, 3}. The edges are: A-1, A-2, B-1, B-3, C-2, C-3. Since this is a bipartite graph, we can color it using two colors.

A bipartite graph is a graph where the vertex set can be divided into two disjoint sets, such that no two vertices within the same set are adjacent. Edges only connect vertices from one set to the other.

Graph:

• Vertices: A, B, C, 1, 2, 3
• Edges: A-1, A-2, B-1, B-3, C-2, C-3

Chromatic Number: 2

Challenges in Finding the Chromatic Number

Determining the chromatic number of a graph can be challenging, particularly for arbitrary graphs. Some major challenges are −

• NP-hardness: Finding the chromatic number is an NP-hard problem, meaning that there is no known algorithm to find the chromatic number for all graphs.
• Complexity for Large Graphs: For large graphs, calculating the chromatic number can be difficult due to the vast number of possible colorings that must be considered.
• Inapproximability: For some graphs, the chromatic number cannot be approximated within a reasonable factor, making it even harder to find a solution.