
- Graph Theory - Home
- Graph Theory - Introduction
- Graph Theory - History
- Graph Theory - Fundamentals
- Graph Theory - Applications
- Types of Graphs
- Graph Theory - Types of Graphs
- Graph Theory - Simple Graphs
- Graph Theory - Multi-graphs
- Graph Theory - Directed Graphs
- Graph Theory - Weighted Graphs
- Graph Theory - Bipartite Graphs
- Graph Theory - Complete Graphs
- Graph Theory - Subgraphs
- Graph Theory - Trees
- Graph Theory - Forests
- Graph Theory - Planar Graphs
- Graph Theory - Hypergraphs
- Graph Theory - Infinite Graphs
- Graph Theory - Random Graphs
- Graph Representation
- Graph Theory - Graph Representation
- Graph Theory - Adjacency Matrix
- Graph Theory - Adjacency List
- Graph Theory - Incidence Matrix
- Graph Theory - Edge List
- Graph Theory - Compact Representation
- Graph Theory - Incidence Structure
- Graph Theory - Matrix-Tree Theorem
- Graph Properties
- Graph Theory - Basic Properties
- Graph Theory - Coverings
- Graph Theory - Matchings
- Graph Theory - Independent Sets
- Graph Theory - Traversability
- Graph Theory Connectivity
- Graph Theory - Connectivity
- Graph Theory - Vertex Connectivity
- Graph Theory - Edge Connectivity
- Graph Theory - k-Connected Graphs
- Graph Theory - 2-Vertex-Connected Graphs
- Graph Theory - 2-Edge-Connected Graphs
- Graph Theory - Strongly Connected Graphs
- Graph Theory - Weakly Connected Graphs
- Graph Theory - Connectivity in Planar Graphs
- Graph Theory - Connectivity in Dynamic Graphs
- Special Graphs
- Graph Theory - Regular Graphs
- Graph Theory - Complete Bipartite Graphs
- Graph Theory - Chordal Graphs
- Graph Theory - Line Graphs
- Graph Theory - Complement Graphs
- Graph Theory - Graph Products
- Graph Theory - Petersen Graph
- Graph Theory - Cayley Graphs
- Graph Theory - De Bruijn Graphs
- Graph Algorithms
- Graph Theory - Graph Algorithms
- Graph Theory - Breadth-First Search
- Graph Theory - Depth-First Search (DFS)
- Graph Theory - Dijkstra's Algorithm
- Graph Theory - Bellman-Ford Algorithm
- Graph Theory - Floyd-Warshall Algorithm
- Graph Theory - Johnson's Algorithm
- Graph Theory - A* Search Algorithm
- Graph Theory - Kruskal's Algorithm
- Graph Theory - Prim's Algorithm
- Graph Theory - Borůvka's Algorithm
- Graph Theory - Ford-Fulkerson Algorithm
- Graph Theory - Edmonds-Karp Algorithm
- Graph Theory - Push-Relabel Algorithm
- Graph Theory - Dinic's Algorithm
- Graph Theory - Hopcroft-Karp Algorithm
- Graph Theory - Tarjan's Algorithm
- Graph Theory - Kosaraju's Algorithm
- Graph Theory - Karger's Algorithm
- Graph Coloring
- Graph Theory - Coloring
- Graph Theory - Edge Coloring
- Graph Theory - Total Coloring
- Graph Theory - Greedy Coloring
- Graph Theory - Four Color Theorem
- Graph Theory - Coloring Bipartite Graphs
- Graph Theory - List Coloring
- Advanced Topics of Graph Theory
- Graph Theory - Chromatic Number
- Graph Theory - Chromatic Polynomial
- Graph Theory - Graph Labeling
- Graph Theory - Planarity & Kuratowski's Theorem
- Graph Theory - Planarity Testing Algorithms
- Graph Theory - Graph Embedding
- Graph Theory - Graph Minors
- Graph Theory - Isomorphism
- Spectral Graph Theory
- Graph Theory - Graph Laplacians
- Graph Theory - Cheeger's Inequality
- Graph Theory - Graph Clustering
- Graph Theory - Graph Partitioning
- Graph Theory - Tree Decomposition
- Graph Theory - Treewidth
- Graph Theory - Branchwidth
- Graph Theory - Graph Drawings
- Graph Theory - Force-Directed Methods
- Graph Theory - Layered Graph Drawing
- Graph Theory - Orthogonal Graph Drawing
- Graph Theory - Examples
- Computational Complexity of Graph
- Graph Theory - Time Complexity
- Graph Theory - Space Complexity
- Graph Theory - NP-Complete Problems
- Graph Theory - Approximation Algorithms
- Graph Theory - Parallel & Distributed Algorithms
- Graph Theory - Algorithm Optimization
- Graphs in Computer Science
- Graph Theory - Data Structures for Graphs
- Graph Theory - Graph Implementations
- Graph Theory - Graph Databases
- Graph Theory - Query Languages
- Graph Algorithms in Machine Learning
- Graph Neural Networks
- Graph Theory - Link Prediction
- Graph-Based Clustering
- Graph Theory - PageRank Algorithm
- Graph Theory - HITS Algorithm
- Graph Theory - Social Network Analysis
- Graph Theory - Centrality Measures
- Graph Theory - Community Detection
- Graph Theory - Influence Maximization
- Graph Theory - Graph Compression
- Graph Theory Real-World Applications
- Graph Theory - Network Routing
- Graph Theory - Traffic Flow
- Graph Theory - Web Crawling Data Structures
- Graph Theory - Computer Vision
- Graph Theory - Recommendation Systems
- Graph Theory - Biological Networks
- Graph Theory - Social Networks
- Graph Theory - Smart Grids
- Graph Theory - Telecommunications
- Graph Theory - Knowledge Graphs
- Graph Theory - Game Theory
- Graph Theory - Urban Planning
- Graph Theory Useful Resources
- Graph Theory - Quick Guide
- Graph Theory - Useful Resources
- Graph Theory - Discussion
Graph Theory - Fundamentals
Fundamentals of Graph Theory
Graph theory is a branch of mathematics that studies graphs, which are structures made of vertices (also called nodes) connected by edges (also called links).
A graph is a diagram of points (vertices) and lines (edges) connected to the points. It has at least one line joining a set of two vertices, with no vertex connecting itself.
The concept of graphs in graph theory stands up on some basic terms such as point, line, vertex, edge, degree of vertices, properties of graphs, etc. Here, in this chapter, we will cover these fundamentals of graph theory.
Point
A point is a specific position in a space, often denoted by a letter. It has no dimensions and serves as a building block in graph theory. Points are the fundamental units that form the vertices of a graph.
Example: Representation of a Point
The dot here represents a point labeled 'a' in the following image −

Line
A line is the connection between two points. In the context of graph theory, lines are referred to as edges when they connect vertices. Lines are important as they represent the relationships or paths between the vertices in a graph.
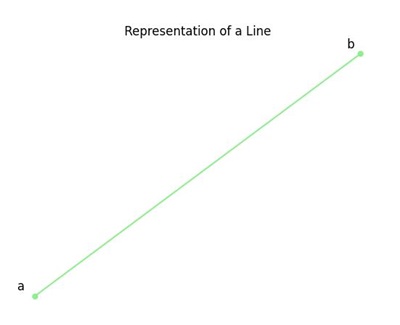
Example: Representation of a Line
The line between points 'a' and 'b' represents the connection between them −
Vertex (Node)
A vertex is a point where edges meet. Vertices are also called nodes and represent the entities in a graph. Each vertex is usually denoted by an alphabetic label. In a graph, vertices are the primary units that are connected by edges.
Example: Representation of a Vertex
In the following image, the vertex is labeled as 'a' −

Edge (Link)
An edge is a line connecting two vertices. Edges represent the relationships between the vertices in a graph. A graph can have many edges connecting different pairs of vertices. Edges can be directed or undirected, weighted or unweighted, depending on the nature of the graph.
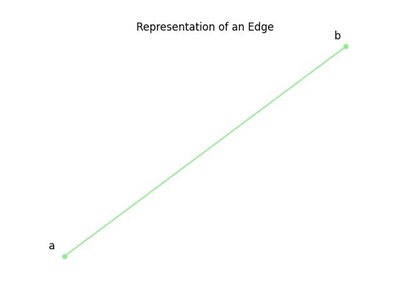
Example: Representation of an Edge
The edge connecting vertices 'a' and 'b' represents the relationship between them −
Graph
A graph is a collection of vertices and edges. It is mathematically represented as G = (V, E), where V is the set of vertices and E is the set of edges. A graph can have various properties based on its structure and connections, such as being directed or undirected, simple or complex, weighted or unweighted.
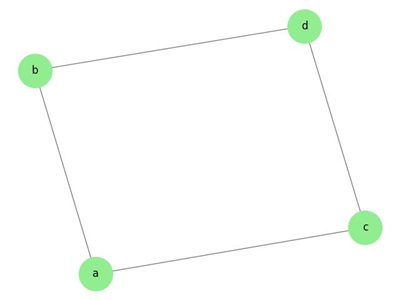
Example: Simple Graph
The graph in this image has vertices 'a', 'b', 'c', and 'd', and edges 'ab', 'ac', 'cd', and 'bd' −
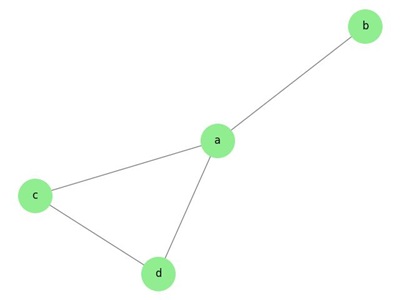
Example: Vertices of the Graph
This graph shows vertices 'a', 'b', 'c', and 'd', with edges 'ab', 'ac', 'ad', and 'cd' −
Loop
A loop occurs when an edge connects a vertex to itself. This type of edge is not allowed in simple graphs but is common in multigraphs. Loops indicate a relationship where an entity is connected to itself, often representing a feedback loop or self-relation.
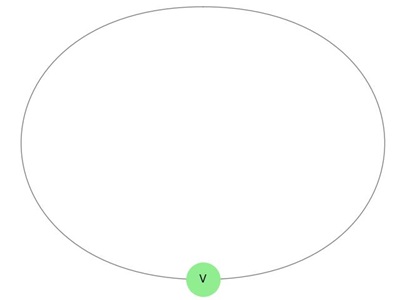
Example: Single Loop
Here, the edge forms a loop at vertex 'V', connecting 'V' to itself −
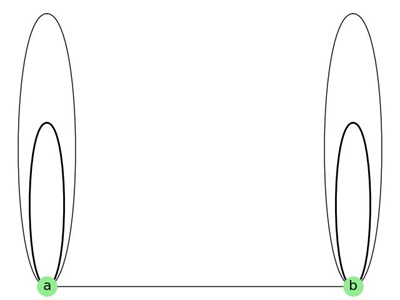
Example: Multiple Loops
This graph contains four loops, two at vertex 'a' and another two at vertex 'b' −
Degree of Vertex
The degree of a vertex is the number of edges incident to that vertex. In simple graphs, the degree is the number of edges connected to a vertex, while in directed graphs, it is divided into indegree (edges coming into the vertex) and outdegree (edges going out from the vertex). The degree of a vertex provides details into its connectivity within the graph.
Notation deg(V)
In a simple graph with n number of vertices, the degree of any vertices is −
deg(v) n 1 v G
A vertex can form an edge with all other vertices except by itself. So the degree of a vertex will be up to the number of vertices in the graph minus 1. This 1 is for the self-vertex as it cannot form a loop by itself. If there is a loop at any of the vertices, then it is not a Simple Graph.
Degree of Vertex in an Undirected Graph
In an undirected graph, edges have no direction, and the degree of a vertex is simply the number of edges connected to it. This measure helps understand the level of connectivity each vertex has in the network.
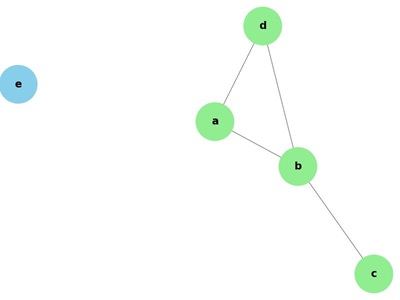
Example
In this graph, the degree of each vertex is −
- deg(a) = 2 (edges 'ab' and 'ad')
- deg(b) = 3 (edges 'ab', 'bd', and 'bc')
- deg(c) = 1 (edge 'bc'). So 'c' is a pendent vertex.
- deg(d) = 2 (edges 'ad' and 'bd')
- deg(e) = 0 (no edges). So 'e' is an isolated vertex.
Degree of Vertex in a Directed Graph
In directed graphs, the degree of a vertex is split into indegree and outdegree. Indegree is the number of incoming edges to a vertex, while outdegree is the number of outgoing edges from it. This distinction is important for understanding the flow of information or resources in the graph.
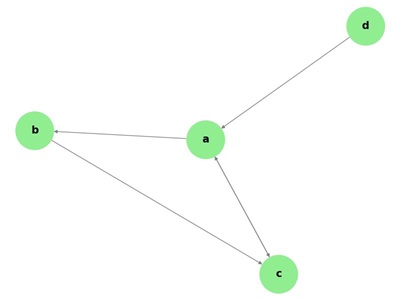
Example
In the above directed graph −
In-degree of each vertex:
- Node a: In-degree = 2 ('ca' and 'da')
- Node b: In-degree = 1 ('ab')
- Node c: In-degree = 2('bc' and 'ac')
- Node d: In-degree = 0
Out-degree of each vertex:
- Node a: Out-degree = 2('ab' and 'ac')
- Node b: Out-degree = 1('bc')
- Node c: Out-degree = 1('ca')
- Node d: Out-degree = 1('da')
Types of Graphs
Graphs come in various types, each with different properties and uses. The major types of graphs are −
- Undirected Graph: A graph where edges have no direction. The relationship between vertices is bidirectional.
- Directed Graph (Digraph): A graph where edges have a direction, representing unidirectional relationships.
- Weighted Graph: A graph where edges have weights, typically representing costs, distances, or capacities.
- Unweighted Graph: A graph where all edges are equal, with no specific weights assigned.
- Simple Graph: A graph with no loops or multiple edges between the same pair of vertices.
- Multigraph: A graph that allows multiple edges between the same pair of vertices.
- Bipartite Graph: A graph where vertices can be divided into two sets, with no edges within the same set.
- Complete Graph: A graph where every pair of vertices is connected by an edge.

Graph Representation
Graphs can be represented in different ways, depending on the problem or algorithm being applied. Some common methods are:
- Adjacency Matrix: A square matrix where each element at row i and column j is 1 if there is an edge between vertex i and vertex j, and 0 otherwise.
- Adjacency List: A collection of lists where each list represents a vertex and contains its adjacent vertices.
- Incidence Matrix: A matrix that represents the relationship between vertices and edges, where each row corresponds to a vertex and each column corresponds to an edge.

In this image,
Adjacency List: 1: [2] 2: [1, 3] 3: [2, 4] 4: [3, 5] 5: [4] Adjacency Matrix: [[0. 1. 0. 0. 0.] [1. 0. 1. 0. 0.] [0. 1. 0. 1. 0.] [0. 0. 1. 0. 1.] [0. 0. 0. 1. 0.]] Incidence Matrix: [[1. 0. 0. 0.] [1. 1. 0. 0.] [0. 1. 1. 0.] [0. 0. 1. 1.] [0. 0. 0. 1.]]