- Reasoning - Home
- Reasoning - Overview
- Reasoning
Missing Characters Online Quiz
Following quiz provides Multiple Choice Questions (MCQs) related to Missing Characters. You will have to read all the given answers and click over the correct answer. If you are not sure about the answer then you can check the answer using Show Answer button. You can use Next Quiz button to check new set of questions in the quiz.

Answer : C
Explanation
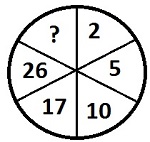
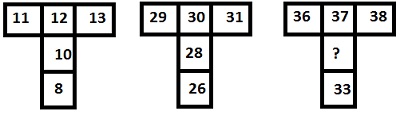
In each step, consecutive prime numbers are added as 2 + 3 = 5, 5 + 5 = 10, 10 + 7 = 17, 17 + 9 = 26 similarly 26 + 11 = 37
Answer : A
Explanation
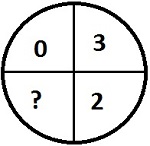
In the above figure, it is clear that numbers are changing as 22 - 1 = 3, 22 - 2 = 2, 22 - 3 = 1, 22 - 4 = 0
Answer : D
Explanation
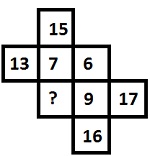
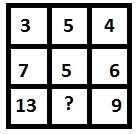
At the end of each of rows and columns are obtain by adding the numbers in same row or column, as 6 + 7 = 13 and 6 + 9 = 15. Hence it can be conclude that 8 is the missing number.
Answer : D
Explanation
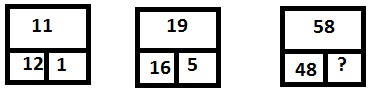
The number at the top are obtained as, 12 + 1 - 2 = 11 and 16 + 5 - 2 = 19 similarly 48 + 12 - 2 = 58.
Answer : C
Explanation
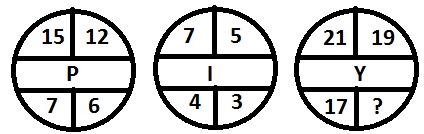
It can be seen from figure that (15 - 12) + (7 - 6) = 4 = 16 = P and (7 - 5) + (4 - 3) = 3 = 9, similarly (21 - 19) + (17 - 14) = 5 = 25 = Y.
Answer : C
Explanation
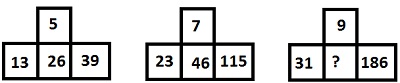
we have $\frac{26+39}{13} = 5$ and $\frac{46+115}{23} = 7$, similarly $\frac{186+93}{31} = 9$, so that missing number is 93.
Answer : B
Explanation
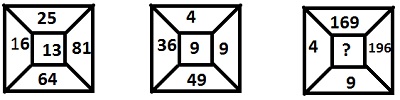
Number at the centre is obtain as, $\sqrt{16} + \sqrt{81}= \sqrt{25}+\sqrt{64}= 13$ and $\sqrt{36} + \sqrt{9}= \sqrt{4}+\sqrt{49}= 9$, similarly $\sqrt{169} + \sqrt{9}= \sqrt{4}+\sqrt{196}= 16$. Therefore missing number is 16.
Answer : C
Explanation
The number is decreasing from top to bottom by 2, therefore 35 must be the missing number.
Answer : B
Explanation
It is clear that (1st column 2nd column) ÷ 2 = number in 3rd column. Therefore missing number = (13 -?)÷ 2 = 9, which gives ? = 5.
Answer : C
Explanation
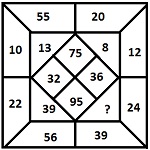
The number are obtained by dividing the pair of numbers by 5, 4, 3, and 2 in clockwise direction and added as $\frac{55}{5} + \frac{10}{5} = 13, \frac{20}{4} + \frac{12}{4} = 8, \frac{22}{2} + \frac{56}{2} = 39$, therefore missing number can be calculated as $\frac{39}{3} + \frac{24}{3} = 21$. Other numbers in the rhombus are obtained by addition of numbers around as 55 + 20 = 75 and so on.