
- Reasoning - Home
- Reasoning - Overview
- Reasoning
Reasoning - Cube and Cuboid
Nowadays, questions based on Cubes and Cuboids are being asked in almost every competitive exam. These problems are very frequent in various competitive exams.
The methods described below are simple yet elegant. They should be very easy to understand and with a little practice you should master them. A cube is a three dimensional solid having 6 faces, 12 edges, and corners. All edges of a cube are equal and all the faces are square in shape. That is a solid figure which has 6 faces; each face being a square is called a cube. If each of the six faces be a rectangle, it is called cuboid. A cuboid is also called a rectangular parallelepiped.
The questions asked on cube and cuboids may be of the following types.
Type I
Several views of a complete cube are given and you have to find which part of the cube lies exactly below a particular part.
Type II
An opened-up cube is given and you have to predict what it will look like when it is closed into a cube.
Type III
A cube could not be varnished on or some of its faces with the same colour or different colours and then cut into a certain specified number of identical pieces. Then question of the form- how many small cubes have 2 faces varnished? How many small cubes have only one face varnished? etc.
There are two types of problems that appear in exam. At first, you are given several views of a complete cube, and you have to state which part of the cube lies exactly below a particular part. In another type, you are given an opened-up cube, and you have to predict what it will look like when it is closed into a cube.
For Example −
Several faces of a cube are shown below −

Which number would lie opposite to 2?
A − 1
B − 6
C − 5
D − 4
The fundamental approach is as follows −
Type I
A fundamental rule: Opposite cannot be together;
Whenever we see a cube, with only three of its faces visible to us, we can never see two opposite faces together. With all this rules, we can easily solve the type of problem discussed above. In the above question where we have to find opposite face of a particular face, we can eliminate those faces which have occurred together with X in any view. Thus, we can eliminate all other choice and remaining will be our answer.
At this point, you should go through the previous paragraph once more and see that you understand the concept. After this, you should try to solve the above example and see if you can apply the concept discussed above. However, you find that you have not understood the concept fully, no problem. Continue reading this section. Things will become clear once you finish the section. With the foregoing fundamental rule at the back of your mind, you can solve the above type of question.
For the question, the rule is sufficient in itself. After that, you can solve it more quickly by three secondary rules.
Solution for above example −
In the given example, we have to find the face opposite 2. Now in the first figure, 2 is appearing along with 1 and 3. It means that neither 1 nor 3 can be opposite to 2. It means that opposite of 1 we can have either 4 or 5 or 6. Similarly, opposite 3 we can have either 4 or 5 or 6. Now, look at the second figure. Here, 3 and 1 occur together with 5. It means that 5 is opposite to neither 3 nor 1. So, it means that either 4 or 6 is opposite 1 and other is opposite 3 so 5 must be opposite 2. Hence 5 is correct answer.
Some Quicker Rules
Now you must have understood the basic trick of solving such questions. The trick is that you should eliminate those choices which are not possible. For this, you take help of fundamental rule which says that if two faces are opposite to each other, their simultaneous occurrence in one view of the cube is not possible. However, in todays time-precious competitions, merely the concept will not do. You must be able to solve a question quickly. There are some secondary rules for solving questions.
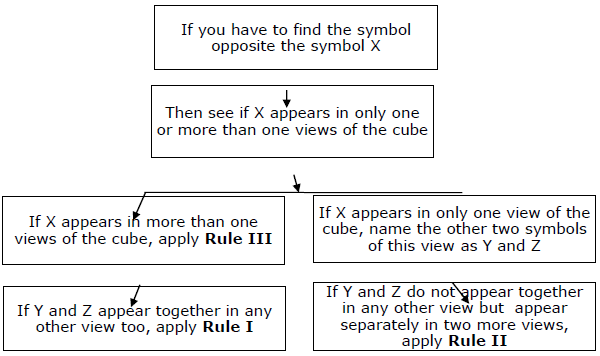
Rule I − Let us call that figure X, the opposite of which you have to find. Suppose in any one view of the cube, X appears with Y and Z. Along with a third figure (say A), then X will be opposite A.
So as for example, you have to find the face opposite 2. (This is our X). Now, 2 appears in one figure along with 1 and 3. (Y and Z). Also 1 and 3 appear together in one more figure, along with 5. (That is A). Hence 2 must be opposite 5.
Rule II − We have to find opposite face of X. Suppose that in any one view of the cube, X appears with Y and Z. Now, suppose Y and Z dont appear together in any more views, but they appear separately in two or more different views. Then the common figure between the two more views in which Y and Z appear separately, will be the figure opposite X.
Rule III − Lets call the figure X, the opposite of which you have to find. Now, suppose X appears in two views and in these two views four different figures are seen with X. Then the only figure not seen with X in these two views must be opposite to X.
Summary − You have to keep the fundamental rule at the back of your mind and then apply three secondary rules for quick answers. The entire approach can be summarised by following diagram.
Type II
In this type, we use fundamental rule. This rule helps us to eliminate those combinations where opposite faces are shown in a single view. So it will lead to the elimination of a choice provided we know how to determine which face will be opposite to each other, by looking at the opened-up cube. For this purpose, there is a very simple rule using which you can tell by looking at the opened-up cube, which faces will be opposite to each other by just looking at it.
The rule is given below;
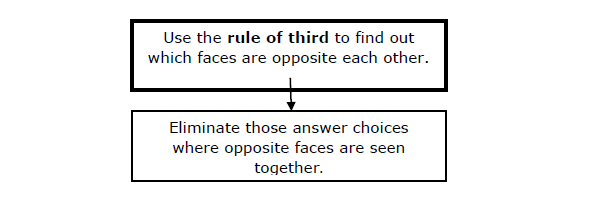
Third is opposite rule −
When you want to find out the opposite face of a face (say X), in figure I, II, III; an opened up cube is given. We have to find which faces opposite each other when the cube is closed.
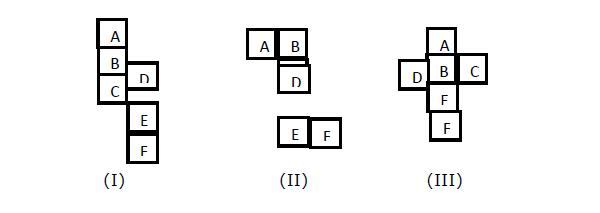
Explanation −
In figure (I), the third figure to A is C. So A is opposite of C. So, D and F will be opposite. B and E will be opposite.
In figure (II), B is third to D, so B will be opposite to D. Similarly, C will be opposite to E and A will be opposite to F.
In figure (III), A is opposite to E, B is opposite F. Hence, C is opposite D.
Steps to solve problem
We can now solve questions of this type. We know how to find the opposite face by looking at an Opened-up cube. We also know that in any view of the cube, opposite faces cant be together. Hence, combining two rules, we can easily solve problems.
Summary
With this, the discussion on how to solve questions of type II is completed. You have to use the rule third to determine which faces are opposite to each other. The following diagram will give the complete information about this approach.
Type III
Counting of Cubes (when a varnished solid cube is cut);
In the previous section, we have discussed the problem of finding the opposite face of a cube. There is another type of question related to cubes wherein a larger cube with different colours varnished on different sides, is broken into several smaller cubes and you have to find the number of cubes having only one side varnished or two sides varnished.
Format of this problem −
Example −
A cube is varnished with three colours green, blue and red on its sides, with every colour varnished on two opposite faces of the cube. Now the cube is broken into 64 cubes of equal size. Based on this information, answer the following questions −
1. How many cubes have two sides varnished and remaining sides unvarnished?
A − 18
B − 20
C − 22
D − 24
2. How many cubes have only one side varnished (with either green or blue colour only)
A − 4
B − 24
C − 16
D − 12
3. How many cubes have no sides varnished?
A − 0
B − 8
C − 12
D − 64