
- Reasoning - Home
- Reasoning - Overview
- Reasoning
Reasoning - Logical Deduction
Logical deduction is an important chapter as many easy and mark fetching questions from this chapter are included in various competitive exams. In this chapter, we will discuss two methods to solve such problems −
- Syllogism method
- Venn diagram method
Basics
If there are two statements, then syllogism will be the best way to solve the problem but if number of statements are more than two, then go for Venn diagram method. Sometimes statements and conclusions are derived from general accepted facts but they can be also non logical. For example −
a) Some chairs are doors.
b) All mans are woman
c) No milk is white
To arrive at the conclusion, abstract thinking is required. One need to understand the logical sense of the sentence then have to answer the conclusions accordingly. Each statement needs to thought as true then we have to verify whether conclusions are logically following the statements.
Qualifiers
These are some of the elementary words that are used to describe how much one thing is similar or different to other. Example of some of the qualifiers are All, Some, Some-not etc.
Venn diagram concept
On the other hand, Venn diagram is a process where we can represent a sentence or statement in the form of geometrical figures. All the given statements are plotted in possible Venn diagrams. Then all conclusions are verified with those diagrams. Any conclusion that satisfies all the Venn diagrams will be considered as a valid conclusion.
| Statements | Corresponding Venn Diagrams |
|---|---|
| All A are B | 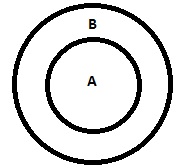 |
| Some A are B (OR) Some A are not B | 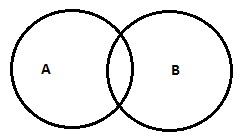 |
| No A is B | 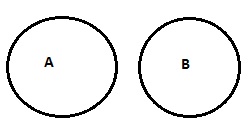 |
Lets take a simple example to understand it in much better way.
Sample − 1
Statements −
All engineers are fools. All fools are doctors. All doctors are poor.
Conclusions −
I. Some poor are fools.
II. Some poor are engineers.
Options −
A − Only I is valid
B − Only II is valid
C − Both the statements are valid
D − None of the statements are valid
Answer − Option C
Explanation −
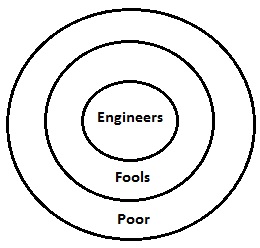
Venn diagram for the given statements is drawn above. It shows all the statements in diagrammatically at one place. Here now if we will discuss about the conclusions one by one, everything will be clear.
Here fools are subset of poor. So it is an obvious fact that some poor will be fools. Hence, conclusion I is valid. Similarly conclusion II is valid as engineers are also a subset of poor. Hence, both the statements will be valid.
Sample − 2
Statements −
Some keyboards are Mouse. Some Mouse are radios.
Conclusions −
I. Some keyboards are radios.
II. Some radios are keyboards
III. All radios are Mouse.
IV. All Mouse are keyboards.
Options −
A − Only conclusion I is valid
B − Only conclusion II is valid
C − Either I or II is valid
D − None of the conclusions is valid
E − Both I and II are valid
Answer − Option D
Explanation − Since both the statements are particular, no definite conclusion is valid.
Sample − 3
Statements −
All students are sober. All students are naughty.
Conclusions −
I. All naughty are either sober or vice-versa.
II. Some sober persons are naughty.
III. Generally naughty are sober.
IV. Crime and guilt go together.
Options −
A − Only conclusion I is valid
B − Only conclusion II is valid
C − Either I or II is valid
D − None of the I or II is valid
E − Both I and II are valid
Answer − Option B
Explanation − Since the intermediate term 'students' is distributed twice in the statements, the conclusion cannot be broad. So, it is valid that 'Some sober persons are naughty'. Thus, II holds true.